電磁力とは 磁界中 で 導体に 電流 が流れた時に受ける 力 をいいます。
電磁力の向きは、フレミングの左手の法則 で知ることができます。
電磁力
電磁力の向き
磁界の中に導体棒を細い電線で、可動するように接続します。
図の向きに電流を流すと
フレミングの左手の法則 による 電磁力 \(F\) が発生します。
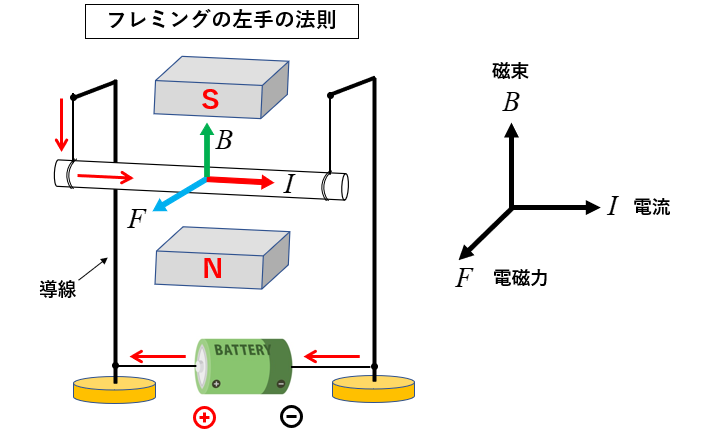
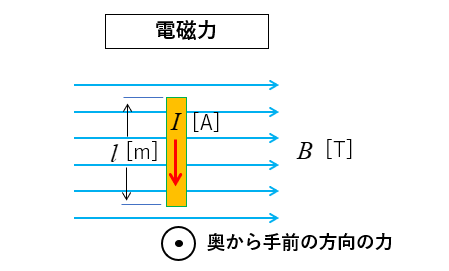
電磁力の大きさ
磁束密度を \(B\) [T]、 電流を \(I\) [A]
磁界中の導体の長さ \(l\) [m] とすると
電磁力の大きさ \(F\) [N] は
\(F=BIl\) [N] になります。
上のような図を描くのは大変なので
平面図で表示すると次のようになります。

磁界中の導体に傾きがある場合
磁界の中にある導体が磁界に対して \(θ\) の傾きがある場合の
導体が受ける電磁力は 導体の長さ \(l\) [m] の垂直分 \(l\sinθ\) になります。
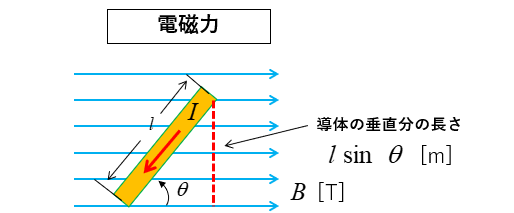
\(F=BIl\sinθ\) [N]
\(B\) [T]\(\cdots\)磁束密度
\(I\) [A]\(\cdots\)電流の大きさ
\(l\) [m]\(\cdots\)導体の長さ
\(θ\) \(\cdots\)導体と磁界の角度
方形コイルに働く電磁力
磁束密度 \(B\) [T] の磁界の中に
長さ \(a\) [m]、 幅 \(b\) [m]、 巻数 \(N\) 回の
方形コイルを磁界と平行になるように置きます。
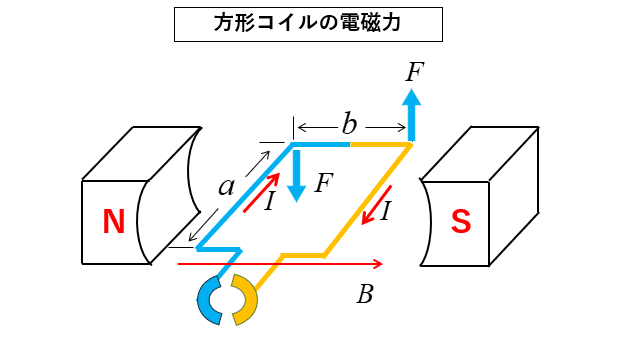
方形コイルに \(I\) [A] の電流を流したときに
コイルにはたらく力は次のようになります。
\(F=BIaN\) [N]
コイルの両端にはたらく力は反対方向になりますので
この回転力つまりトルク \(T\) は次のようになります。
\(T=2\left(F\cfrac{b}{2}\right)=2BIaN\cfrac{b}{2}=BIabN\) [N・m]
\(T=BIabN\) [N・m]
参 考
電磁力の公式はローレンツ力の公式から求めることができます。
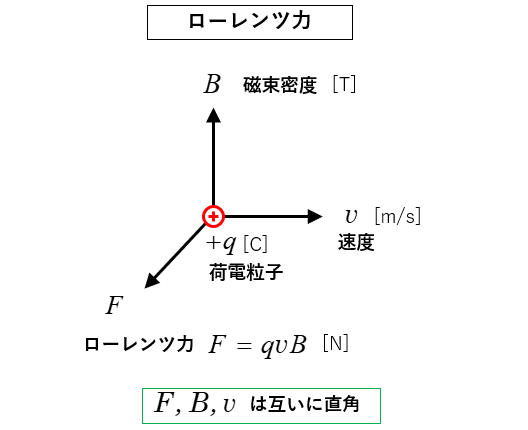
ローレンツ力 は、図のように荷電粒子が磁界中を移動したときに生じる力です。
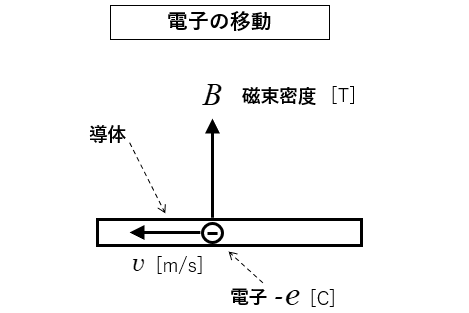
★ 図のように導体の中を 電子 \(-e\) [C] が
速度 \(v\) で 左向き に移動しています。
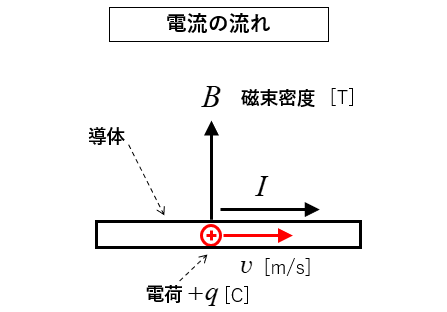
★ 上図で電子が 左向き に移動するということは
プラスの電荷が 右向き に移動する(電流が流れる)と考えることができます。
★ 図のように 磁束密度 \(B\) の中を 荷電粒子 \(q\) が
速度 \(v\) で移動すると 荷電粒子は ローレンツ力 \(F\) を受けます。
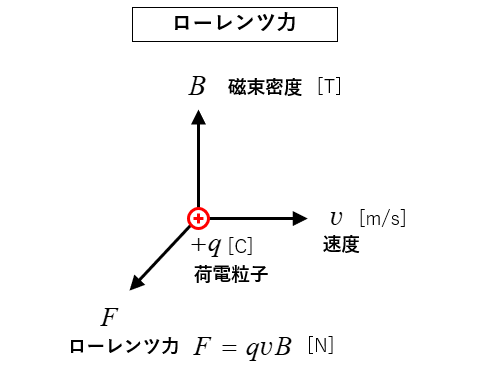
★ 実際に ローレンツ力 を受けるのは 電子 と考えることができます。
電子 1 個が受ける力を \(f\) [N] とすると
\(f=evB\) [N] になります。
電子 1 個が受ける力 \(f\) [N] に
導体を移動する電子の数を掛けると 導体が受ける力 になります。
導体が受ける力 \(F\) [N] は
\(S\) [m2]\(\cdots\) 導体の断面積
\(l\) [m]\(\cdots\) 導体の長さ
\(n\) [m3]\(\cdots\) 電子の個数密度 とすると
\(F=evB×Sln \cdots (1)\) になります。
\(I=Sevn \cdots (2)\) ですから
式(2)を 式(1)に代入します。
電磁力は次のようになります。
\(F=BIl\) [N] \(\cdots (3)\)
磁束密度
\(B=μH\) を式(3)に代入すると
\(F=μHIl\) [N] になります。
練習問題
問題1
図のように 導体ABCを 1辺が \(a\) の正三角形に配置します。
電流 \(I\) を図の向きに流した。
導体Bが受ける単位長さの力を求めよ。
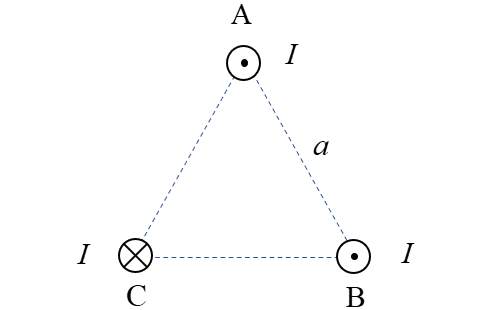

<解答例>
■ 2本の導体の間に働く力の公式
\(F=\cfrac{μI_1I_2}{2πr}\) [N/m]
★ 公式を使うと導体ABには吸引力 \(F_A\) が働きます。
\(F_A=\cfrac{μI^2}{2πa}\) [N/m]
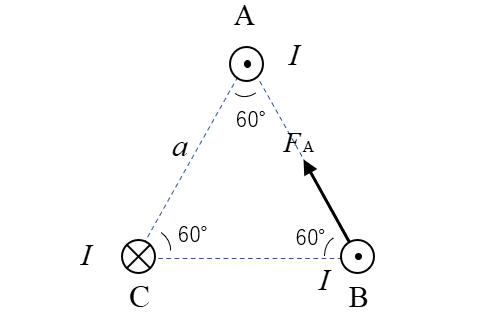
★ 公式を使うと導体BCには斥力 \(F_C\) が働きます。
\(F_C=\cfrac{μI^2}{2πa}\) [N/m]
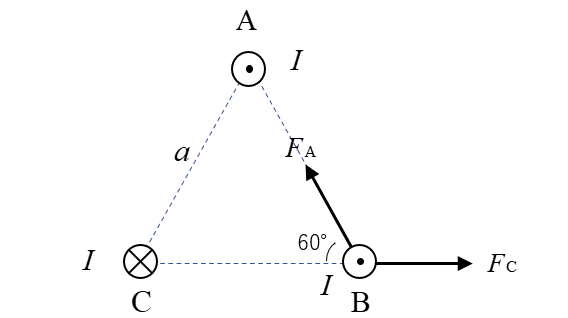
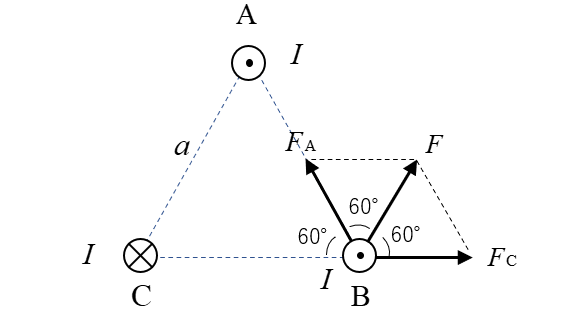
★ ベクトル合成をすると図のようになります。
正三角形なので \(F_A=F_C=F\) から
\(F=\cfrac{μI^2}{2πa}\) [N/m] になります。
別解 電界の強さから求める方法
★ 導体Aの電流による磁界 \(H_A\) は図のようになります。
磁界の方向は半径 \(a\) の円の接線方向になります。
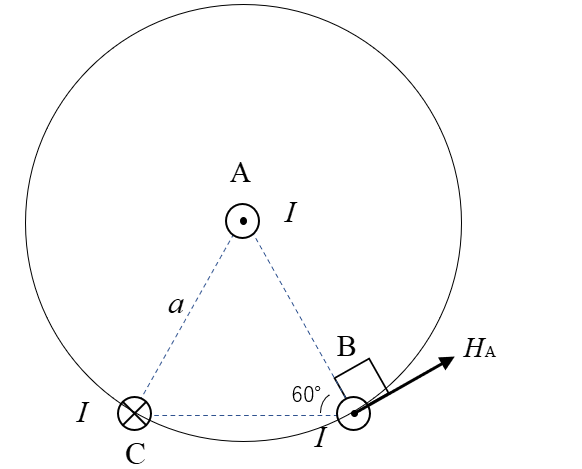
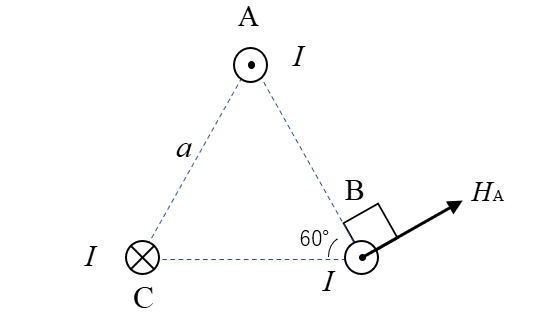
円を消すと次のようになります。
★ 導体Cの電流による磁界 \(H_C\) は図のようになります。
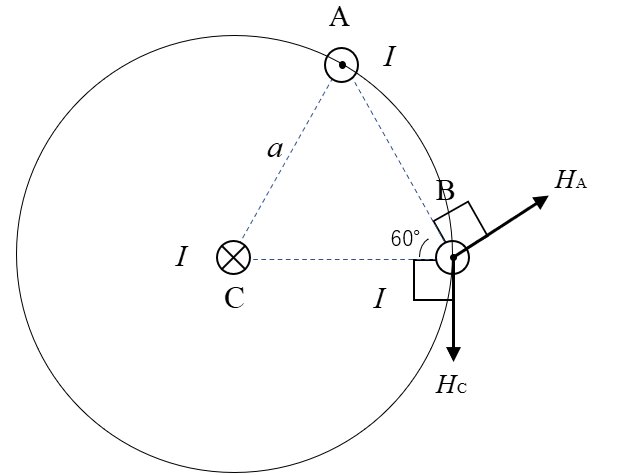
円を消すと次のようになります。
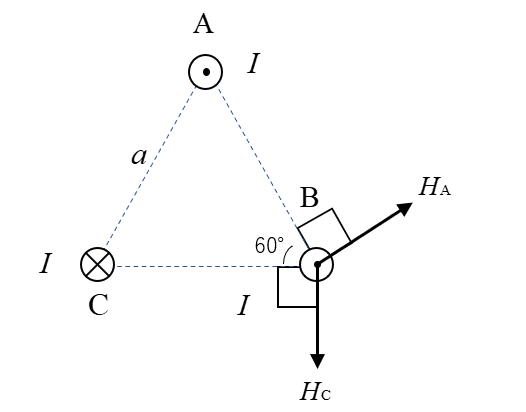
★ ベクトルを合成すると次のようになります。
正三角形なので \(H_A=H_C=H\) になります。
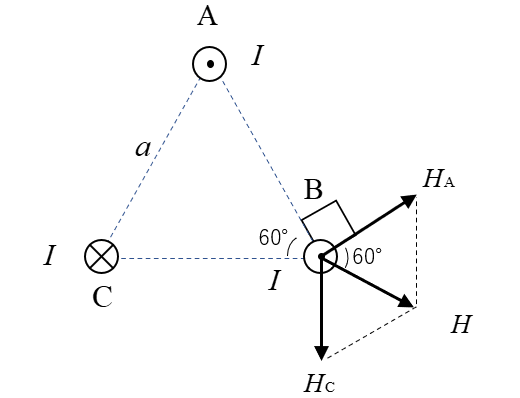
直線電流による磁界の強さ \(H\) は公式から
\(H=\cfrac{I}{2πr}\) なので
\(H=\cfrac{I}{2πa}\) になります。
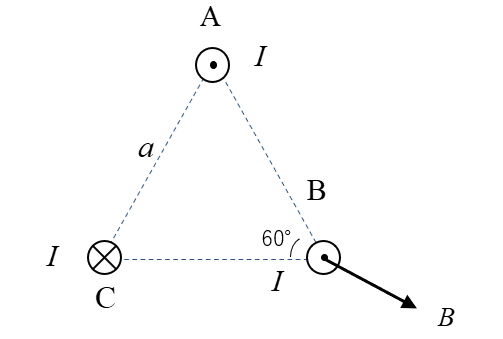
磁束密度 \(B\) は 電界と同じ方向にあるので図のようになります。
フレミングの左手の法則から、図のような向きに電磁力 \(F\) が働きます。
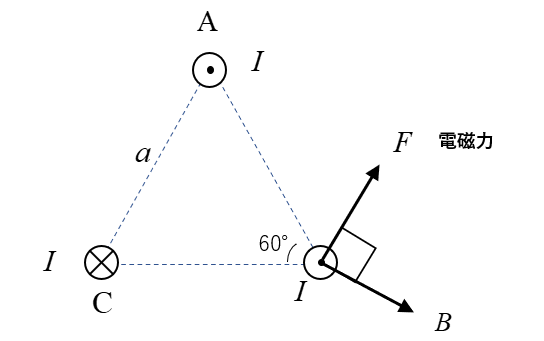
\(F=BIl\) に \(B=μH\) を代入すると
単位長さなので \(l=1\) から
\(F=μHI×1=\cfrac{μI^2}{2πa}\) [N] になります。
以上で「電磁力とフレミングの左手の法則」の説明を終わります。