フレミングの左手の法則と右手の法則

• フレミングの左手の法則の覚え方。
• フレミングの左手の法則の力が生まれるわけ。
• フレミングの右手の法則の覚え方と使い方。

この記事では、フレミングの左手と右手の法則について説明します。

フレミングの左手の法則

フレミングの左手の法則　は、電動機（モーター）の原理を知るのに役立ちます。

つまり、磁界中のコイルに電流を流すと、「どの方向に動くか」を知ることができます。

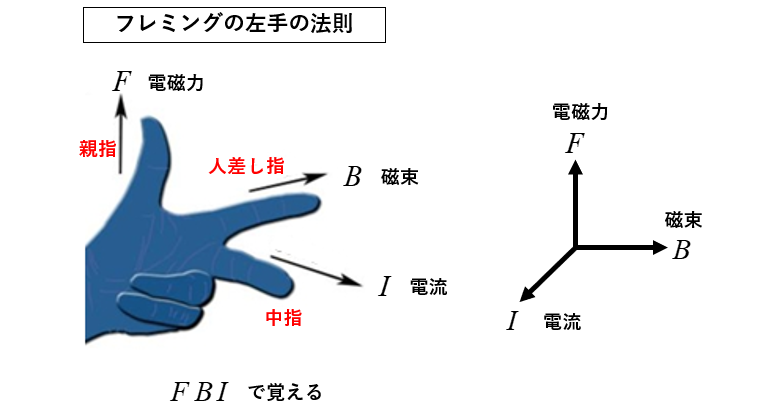
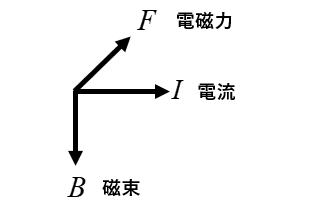
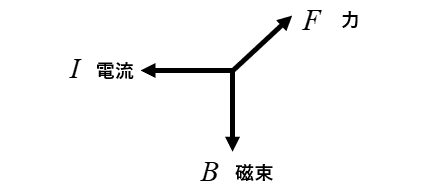
図のように左手の　「親指」「人指し指」「中指」　を互いに直角に立てます。

親指は「電磁力」$F$　の方向

人差し指は「磁束」$B$　の方向

中指は「電流」$I$　の方向を示しています。

親指、人差し指、中指の順に　$FBI$　と覚えたらどうでしょう。

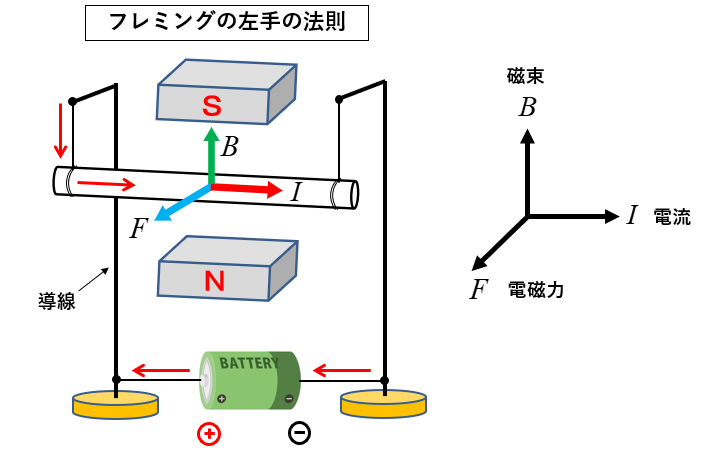
★　フレミングの左手の法則は

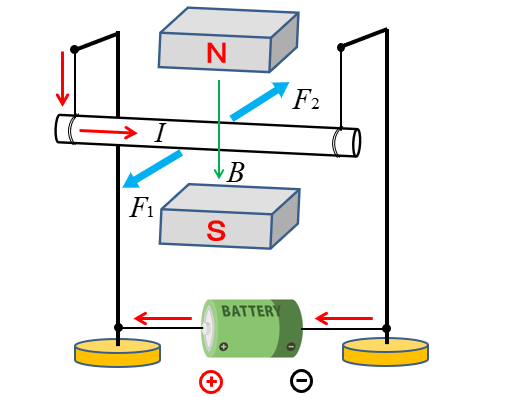
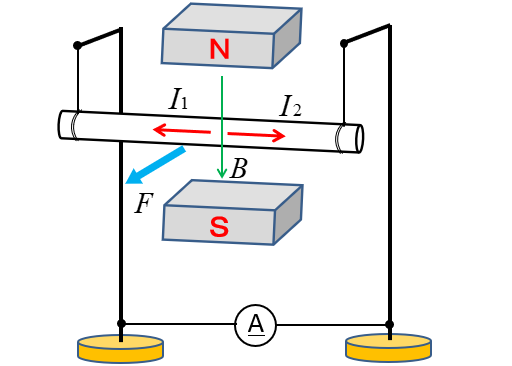
磁界の中にある導体棒に電流を流すと

図のような電磁力が発生します。

★　次の図で、電流と磁界の方向がわかっています。

この場合、導体は　$F_1 \mathrm{と} F_2$　どちらに動くでしょう。

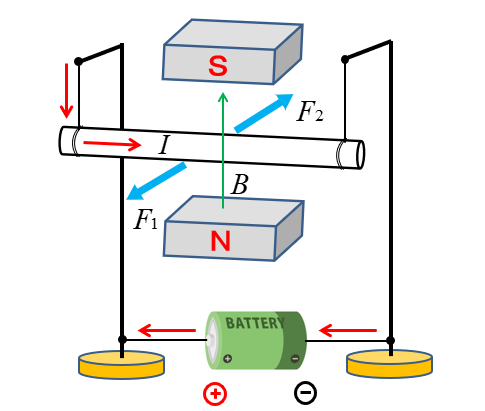
フレミングの左手の法則を当てはめてみると、簡単にわかります。

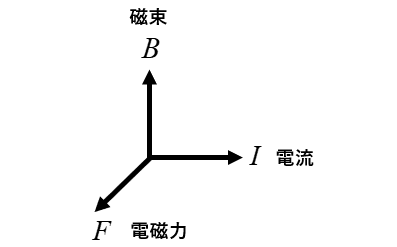
答えは　$F_1$　の方向になります。

■　例　題

１．図は上のものと、「電池」の向きが反対です。

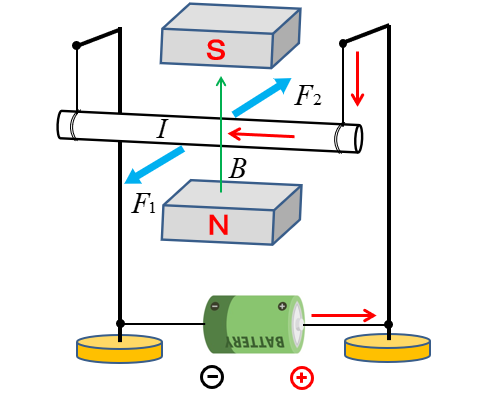
電流の向きが反対ですから

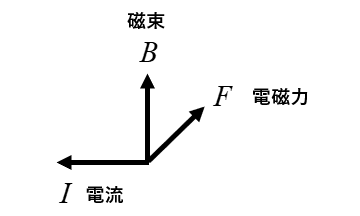
答えは　$F_2$　の方向になります。

２．上の問題と「磁束」の向きが反対です。

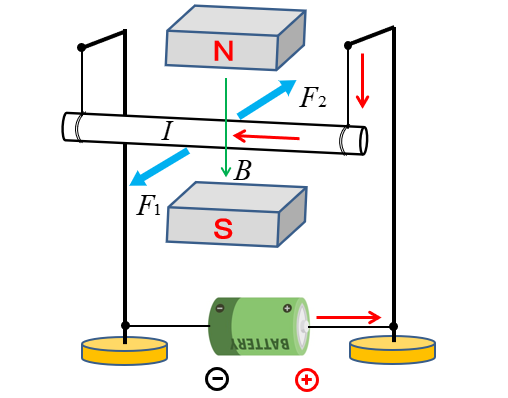
磁束の向きが反対ですから

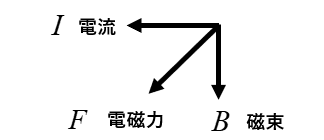
答えは　$F_1$　の方向になります。

３．上の問題と「電池」の向きが反対です。

電流の向きが反対ですから

答えは　$F_2$　の方向になります。

フレミングの左手の法則の力が生まれる理由

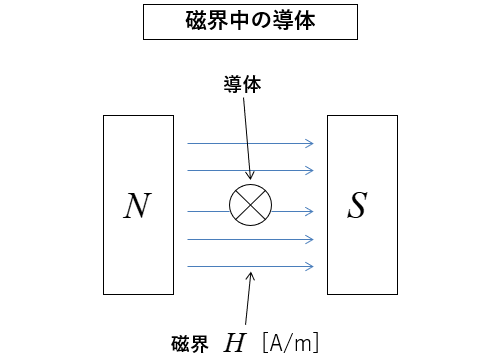
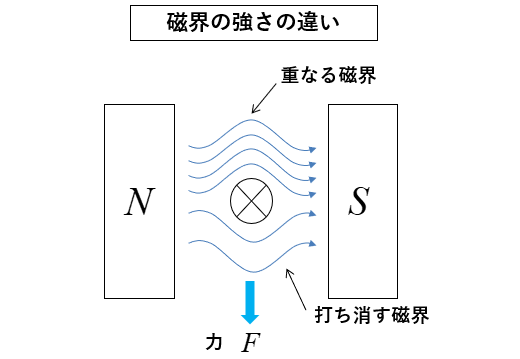
磁界があるところに、導体を置きます。

この図では導体に手前から奥に向かう電流が流れていることを示しています。

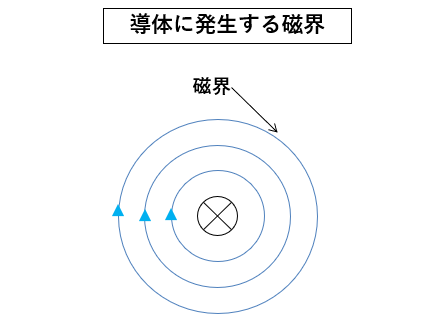
導体に電流を流すと図のような磁界が発生します。

これは　右ねじの法則　の磁界です。

導体の上側では磁石による磁界と電流による磁界が　同じ方向　なので磁界が強くなる。

導体の下側では磁石による磁界と電流による磁界が　打ち消しあう　ので磁界が弱くなる。

その結果、導体を下に押す力が働くことになります。これが力が生まれる理由です。

フレミングの右手の法則

フレミングの右手の法則は、発電機の原理を知るのに役立ちます。

つまり、磁界中のコイルを動かすと　「コイルに起電力」　が発生するのです。

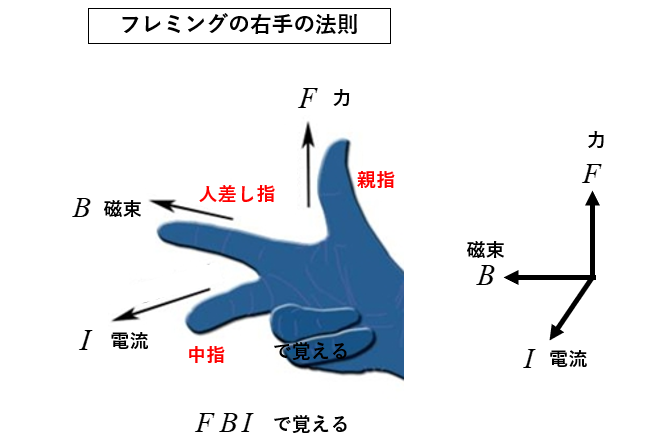
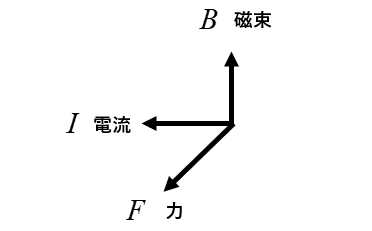
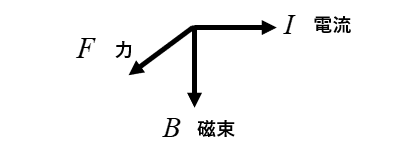
図のように右手の　「親指」「人差し指」「中指」　を互いに直角に立てます。

親指は「力」$F$　の方向

人差し指は「磁束」$B$　の方向

中指は「電流」$I$　の方向を示しています。

親指、人差し指、中指の順に　$FBI$　と覚えたらどうでしょう。

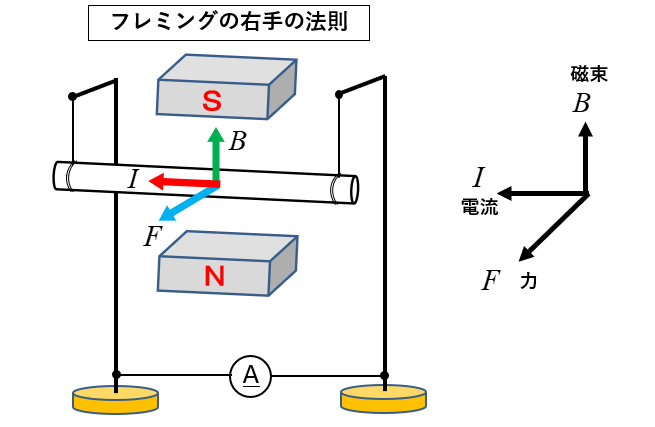
★　フレミングの右手の法則は

磁界の中にある導体棒を移動すると図のような向きの電流が発生します。

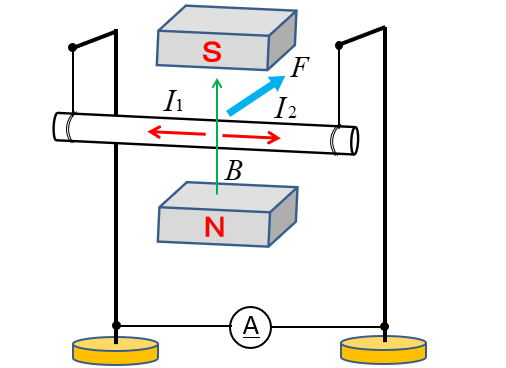
★　次の図で、力（動く方向）と磁界の方向がわかっています。

この場合、電流は　$I_1 \mathrm{と} I_2$　どちらに流れるでしょう。

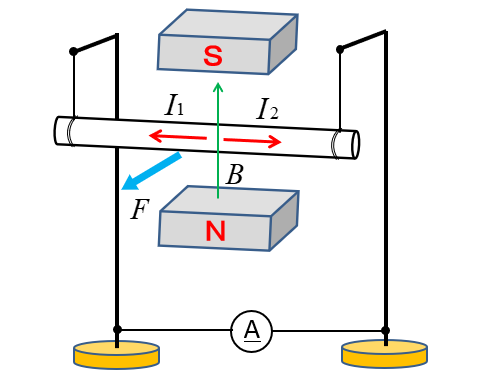
フレミングの右手の法則を当てはめてみると、簡単にわかります。

答えは　$I_1$　の方向になります。

■　例　題

１．図は上のものと、「力」の向きが反対です。

力の向きが反対ですから

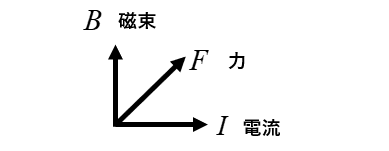
答えは　$I_2$　の方向になります。

２．上の問題と「磁束」の向きが反対です。

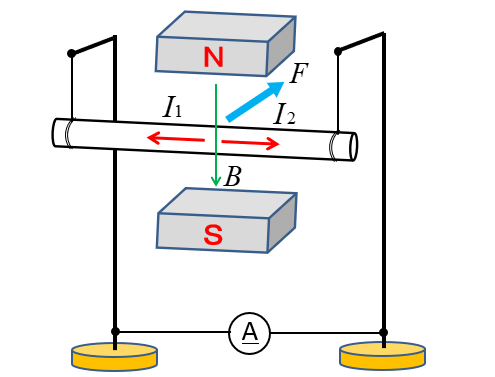
磁束の向きが反対ですから

答えは　$I_1$　の方向になります。

３．上の問題と「力」の向きが反対です。

力の向きが反対ですから

答えは　$I_2$　の方向になります。

以上で「フレミングの左手の法則と右手の法則」の説明を終わります。