- 電磁誘導
- ファラデーの法則
について説明します。
電磁誘導(電磁誘導作用)とは
コイルなどの磁束が変化するときに、誘導起電力が発生する現象をいいます。
ファラデーの法則による誘導起電力の公式を
ファラデーの電磁誘導の法則 といいます。
磁石の移動による電磁誘導
コイルなどに磁石を近づけたり、遠ざけたりするとコイルを切る磁束が変化することで
誘導起電力(誘導電流)が発生します。
誘導起電力の向きを示す法則が レンツの法則 です。

コイルなどの導体が磁束の変化を受けるときに
コイルなどに誘導起電力が発生することを
電磁誘導 あるいは 電磁誘導作用 といいます。
電磁誘導によって発生した起電力を 誘導起電力
流れる電流を 誘導電流 といいます。
磁石による電磁誘導の特徴
- コイルに磁石を近づけたり遠ざけたりして、磁力線が変化した時だけ起電力が発生する。
- コイルを貫く磁束が変化する時だけ、コイルに起電力が発生する。
- この現象を電磁誘導作用といいます。
- 磁石の出し入れを、早くすると起電力は大きくなります。
- 磁石のS極をコイルに近づけると、N極を近づけたときと反対の方向の起電力が発生します。
- コイルからS極を遠ざけるときは、N極を遠ざけた時と反対の方向の起電力が発生します。
これは磁界の向きがN極から出て、S極に入るからです。 - 磁石のN極を近づけたときと、S極を近づけたときでは起電力の方向は反対になります。
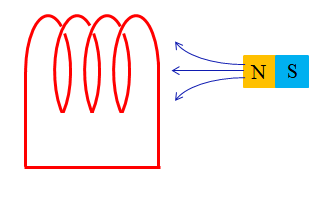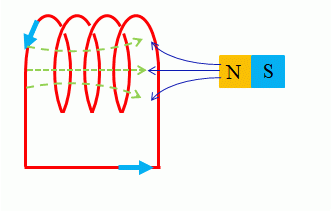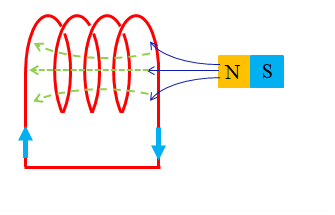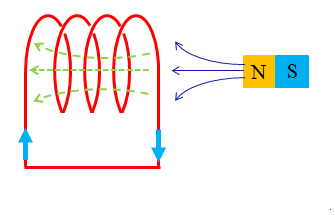
コイルに磁石を近づけるとき
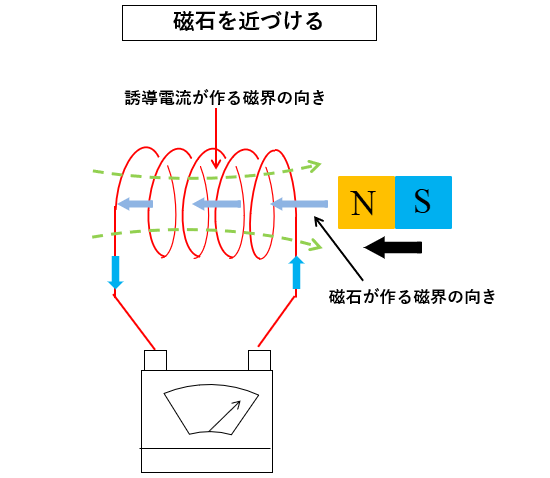
- 磁石のN極をコイルに近づけると、コイルから見ると磁石によってできる磁界は強くなっていきます。
- コイルにはレンツの法則により、磁石の磁界を打ち消す方向に磁界ができます。
- 右向きの緑の点線の磁界ができるためには、コイルには 右ねじの法則 により図のような方向に誘導電流が流れることになります。

コイルから磁石を遠ざけるとき
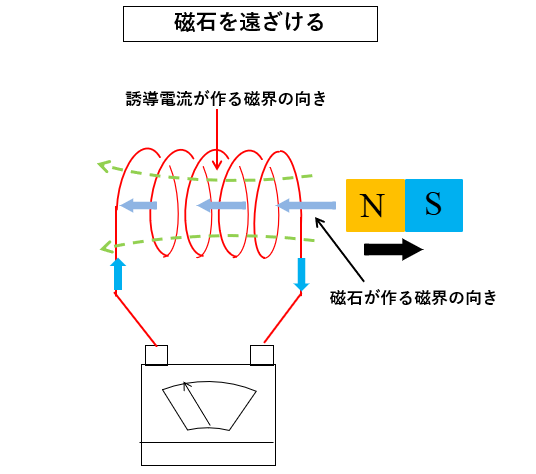
- 磁石のN極をコイルから遠ざけると、コイルから見ると磁石によってできる磁界は弱くなっていきます。
- コイルにはレンツの法則により、磁石の磁界を強くする方向に磁界ができます。
- 左向きの緑の点線の磁界ができるためには、コイルには 右ねじの法則 により図のような方向に誘導電流が流れることになります。
電磁誘導(電磁誘導作用)\(\cdots\)磁気の変化によって起電力が誘導されること。
誘導起電力\(\cdots\)電磁誘導によって発生する起電力のこと。
誘導電流\(\cdots\)誘導起電力によって流れる電流のこと。
導体の移動による電磁誘導
図のように、磁界の中の導体棒を前後に動かすと
上記のコイルのときと同じように電磁誘導が発生します。
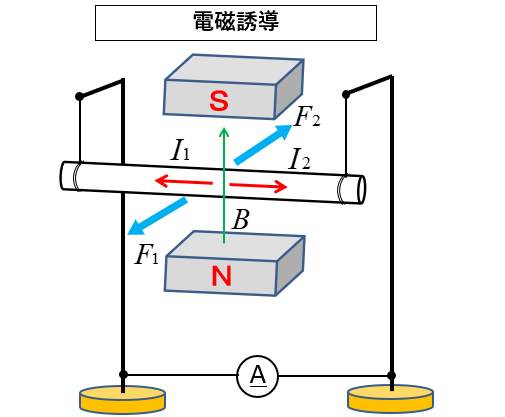
導体棒を \(F_1\) の方向に動かすと \(I_1\) の向きの電流が流れます。
導体棒を \(F_2\) の方向に動かすと \(I_2\) の向きの電流が流れます。
このときに発生する起電力の方向は フレミングの右手の法則 でわかります。
ファラデーの法則
ファラデーの法則は 誘導起電力の大きさ を示す法則です。
★ 図のような磁界の中に導体棒があります。
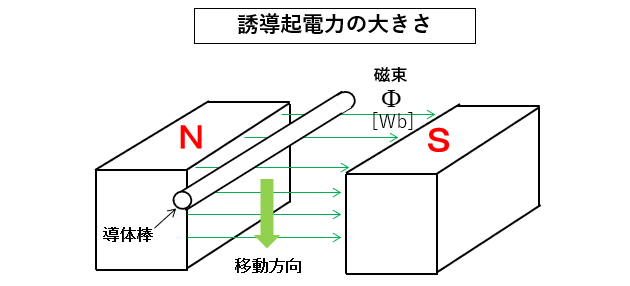
★ 次に導体棒が移動して \(Δt\) [s] 間に \(Δ\Phi\) [Wb] の磁束を切ったとすると
誘導起電力 \(e\) は磁束の時間に対して変化する割合なので
\(e=\cfrac{Δ\Phi}{Δt}\) [V] になります。
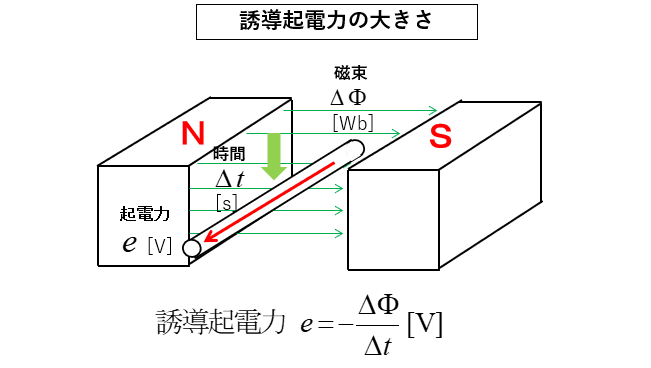
\(e=-\cfrac{Δ\Phi}{Δt}\)
式にマイナスが付いているのは、負の値ということではありません。
本来の磁束と 反対の磁束を発生させる誘導起電力である という意味になります。
コイルの場合
図のような、コイルの場合も同じに考えることができます。
一巻きのコイルを貫く磁束が \(\Phi\) でした。
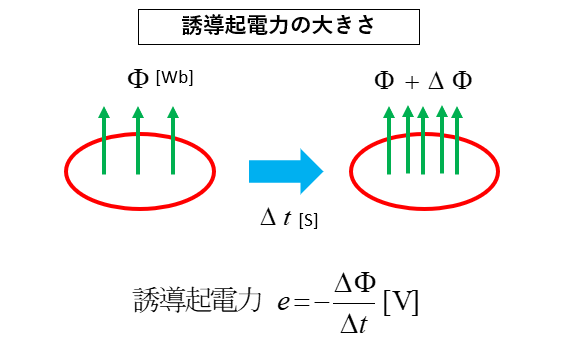
★ Δt秒後の磁束が \(\Phi+Δ\Phi\) に増加したときの誘導起電力は
ファラデーの電磁誘導の法則により次の式になります。
\(e=-\cfrac{Δ\Phi}{Δt}\) [V]
★ コイルの巻数が \(N\) ならば、次のようになります。
\(e=-N\cfrac{Δ\Phi}{Δt}\) [V]
平等磁界中の誘導起電力
磁束密度 \(B\) [T] の平等磁界中の導体 \(l\) [m] を
速度 \(v\) [m/s] で移動したときに発生する 誘導起電力 \(e\) は
\(e=Blv\) [V] になります。
ファラデーの法則と自己インダクタンスの関係
自己インダクタンス \(L\) [H] の \(N\) 巻のコイルに
電流 \(I\) [A] が流れています。
\(Δt\) 秒後に電流が \(ΔI\) [A] 増加し
磁束が \(Δ\Phi\) [Wb] 増加しました。
磁束鎖交数の増加量は
\(NΔ\Phi\) [Wb]\(\cdots(1)\)
自己インダクタンスは、\(L=\cfrac{N\Phi}{I}\) ですから
\(LI=N\Phi\cdots(2)\)
コイルに誘導される起電力は
\(e=-N\cfrac{Δ\Phi}{Δt}\cdots(3)\)
式(3)に式(2)を代入すると、次のようになります。
\(e=-N\cfrac{Δ\Phi}{Δt}\)
\(=-\cfrac{NΔ\Phi}{Δt}\)
\(=-\cfrac{LΔI}{Δt}\)
\(=-L\cfrac{ΔI}{Δt}\) [V]
ファラデーの法則
\(e=-N\cfrac{Δ\Phi}{Δt}\) [V]
\(e=-L\cfrac{ΔI}{Δt}\) [V]
式にマイナスが付いているのは、負の値ということではありません。
本来の磁束と 反対の磁束を発生させる誘導起電力である という意味になります。
練習問題
問題1
20回巻きのコイルに磁石を近づけたところ
1秒間に 0.3 [Wb] の鎖交磁束が変化しました。
このときの誘導起電力 \(e\) [V] を求めよ。
<解答例>
誘導起電力の公式に当てはめると
\(e=-N\cfrac{Δ\Phi}{t}\)
\(e=-20×\cfrac{0.3}{1}=-6\)
誘導起電力
\(e=-6\) [V] になります。
以上で「電磁誘導とファラデーの法則」の説明を終わります。