誘導起電力とは 電磁誘導 により発生する起電力をいいます。
誘導起電力により流れる電流を 誘導電流 といいます。
誘導起電力
誘導起電力の向き
磁界の中で導体棒を移動すると フレミングの右手の法則 による起電力が発生します。

導体棒が直線運動をするときの起電力
磁界 \(B\) [T] と垂直にある長さ \(l\) [m] の導体が
速度 \(v\) [m/s] で直線運動をすると
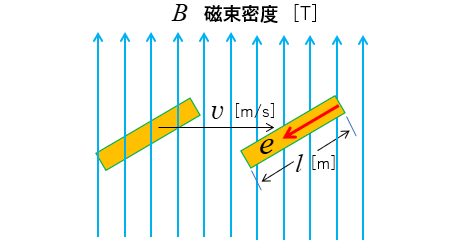
1秒間に導体棒が移動する面積は
\(vl\) [m2]
1秒間に導体棒が切る磁束は、磁束密度×面積です。
\(Blv\) [Wb]
ファラデーの法則から
\(e=\cfrac{Δ\Phi}{Δt}=\cfrac{Blv}{1}=Blv\)
\(e=Blv\) [V] になります。
導体棒が角度θで直線運動をしたときの起電力
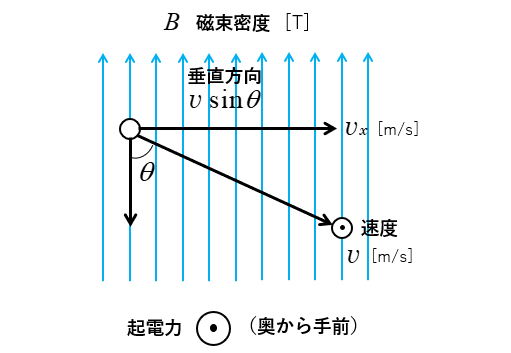
導体棒が角度θで直線運動をしたときの起電力は
磁束と垂直方向の速度が磁束を直角に切ることになります。
垂直方向の速度 \(v_x\) [m/s] は
\(v_x=v\sinθ\) [m/s] になります。
したがって、起電力 \(e\) は奥から手前の向きに発生し、大きさは
\(e=Blv_x=Blv\sinθ\) [V] になります。
参 考
誘導起電力の公式の求め方
電荷に働くローレンツ力は
\(F=qvB\) [N]

ローレンツ力の向きは フレミングの左手の法則 により 図の向きになります。
磁界の中で導体棒に生じる起電力を考えます
導体の中の荷電粒子を考えると、磁界の中で導体棒を
図のように動かすと \(v\) の向きに電流が流れることと同じになります。
したがって 図の向きの ローレンツ力 が生じます。(フレミングの左手の法則)
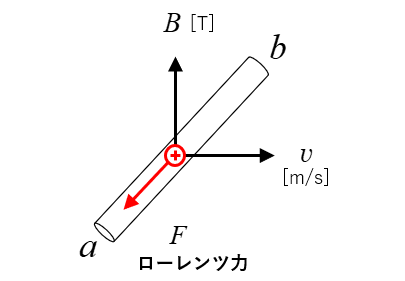
導体の中の荷電粒子はローレンツ力により
\(a\)端にプラスが \(b\)端にマイナスが集まってきます。
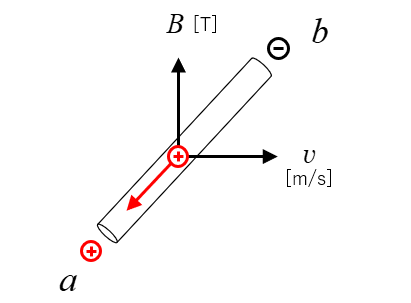
荷電粒子とマイナスの電荷の間には クーロン力 が働くことになります。
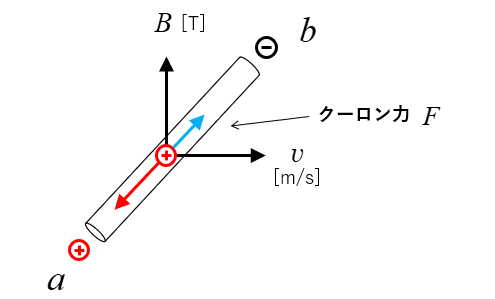
導体を移動させ続けると
やがてローレンツ力とクーロン力が釣り合うことになります。
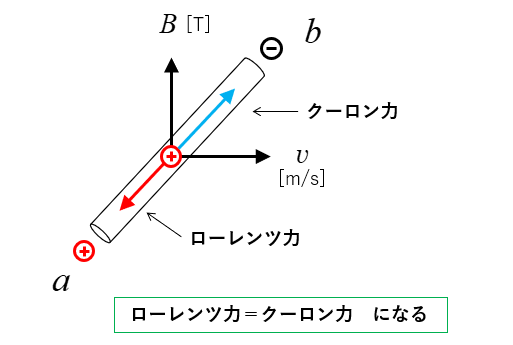
電子の電荷 \(e\) [C] で考えると
ローレンツ力は
\(F=evB\)
クーロン力は電界で表すと
\(F=eE\)
ローレンツ力とクーロン力が等しいので
\(evB=eE\)
\(E=vB\) の電界が導体に発生しています。
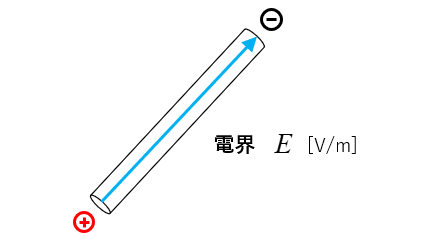
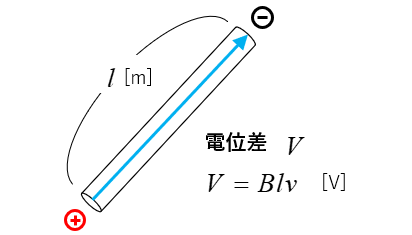
導体の長さを \(l\) [m] とすると \(V=Ed\) の公式から
電位差を \(V\) [V] とすると
\(V=El=vB×l\) [V]
\(V=Blv\) [V] になり 誘導起電力の公式 (1) と同じになります。
以上で「誘導起電力とフレミングの右手の法則」の説明を終わります。