テブナンの定理は、複数の電源や負荷を持つ電気回路の、等価電源と等価抵抗を求めて等価回路に変換する定理です。
等価電源と等価抵抗の等価回路にする理由は、任意の場所に流れる電流をオームの法則で簡単に計算するためです。
テブナンの定理とは

テブナンの定理は、「複雑な電気回路を等価回路」に変換する定理です。テブナンの定理を使うことで、任意の場所の電流を求めることができます。
テブナンの定理
\(I=\cfrac{V_0}{R_0+R}\) [A]
- \(I\)・・・求める電流
- \(V_0\)・・・等価電源
- \(R_0\)・・・等価抵抗
- \(R\)・・・負荷抵抗
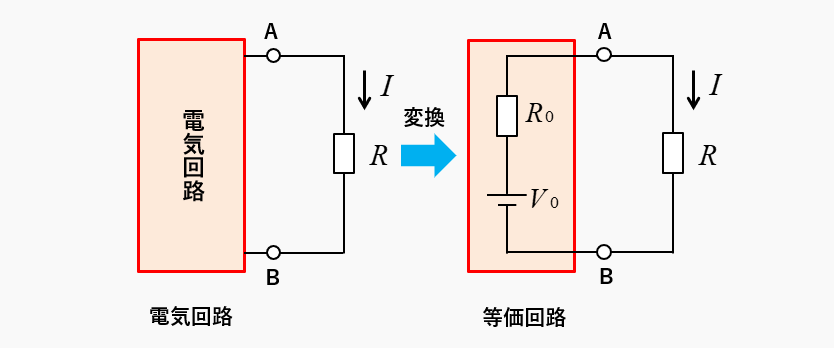
テブナンの定理は、等価電源と等価抵抗を求めて等価回路に変換します。
テブナンの定理の名称について
- 鳳-テブナンの定理(ほう-テブナンのていり)
- ヘルムホルツ-テブナンの定理
- 等価電圧源表示
などの呼び方があります。
テブナンの定理をわかりやすく解説
テブナンの定理の使い方の手順
テブナンの定理の問題
テブナンの定理で、抵抗 \(R\) に流れる電流を求める
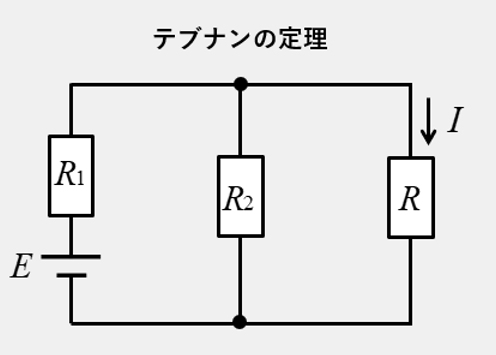
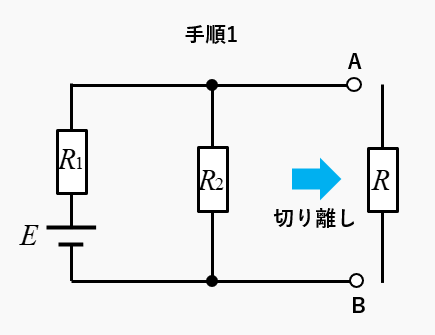
手順1 切り離す
抵抗 \(R\) を切り離す。
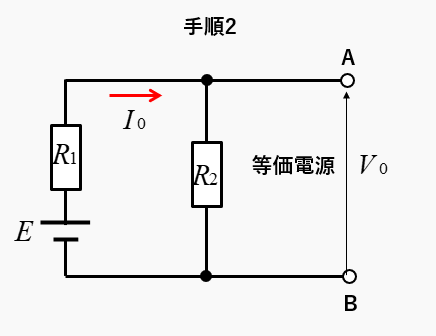
手順2 等価電源を求める
端子AB間の電圧が等価電源 \(V_0\) です。
回路に流れる電流 \(I_0\) を求めて、等価電源 \(V_0\) を求める。
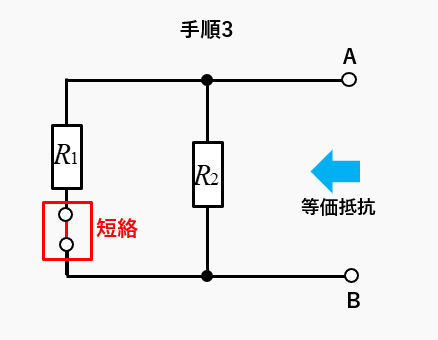
手順3 等価抵抗を求める
電圧源を短絡して、電源を除去する。
端子ABから見た、合成抵抗が等価抵抗です。
等価抵抗
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\)
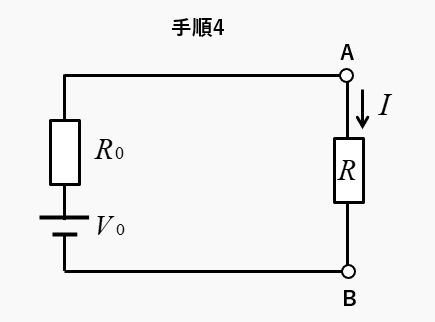
手順4 等価回路に変換
等価電源と等価抵抗を使って、元の回路を等価回路に変換
求める電流 \(I\)
\(I=\cfrac{V_0}{R_0+R}\)
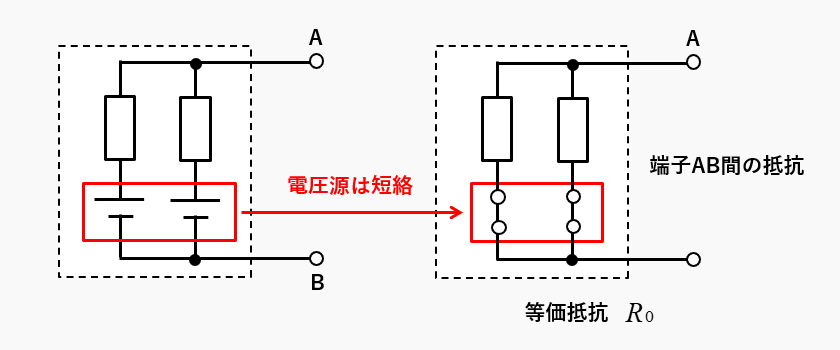
電圧源と電流源の取り扱い方
電圧源は短絡する
回路内部の電圧源をすべて短絡します。端子AB間の合成抵抗が等価抵抗です。
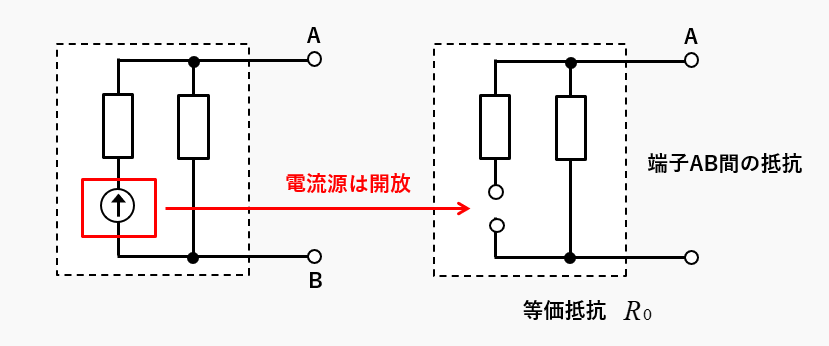
電流源は開放する
回路内部の電流源をすべて開放します。端子AB間の合成抵抗が等価抵抗です。
テブナンの定理の使い方(電圧源)
テブナンの定理
\(I=\cfrac{V_0}{R_0+R}\)
- \(V_0\)・・・等価電源
- \(R_0\)・・・等価抵抗
- \(R\)・・・負荷抵抗
電気回路の電源は、電圧源の場合が一般的です。
電圧源の例題
次の図は、電気回路の 4Ωの抵抗に流れる電流を「テブナンの定理」で求める例題です。
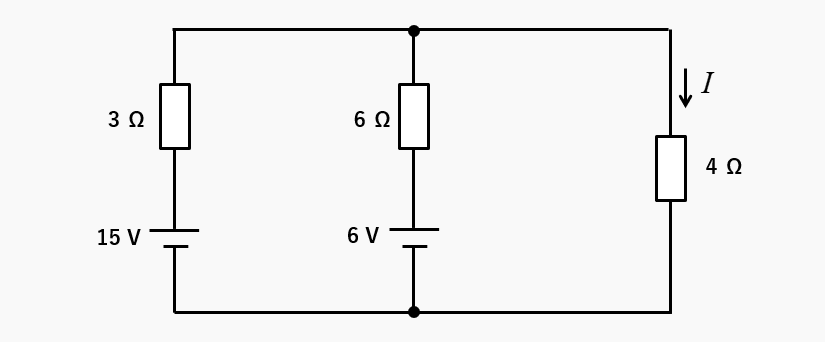
手順1(抵抗を切り離す)
4Ωの抵抗を切り離します。
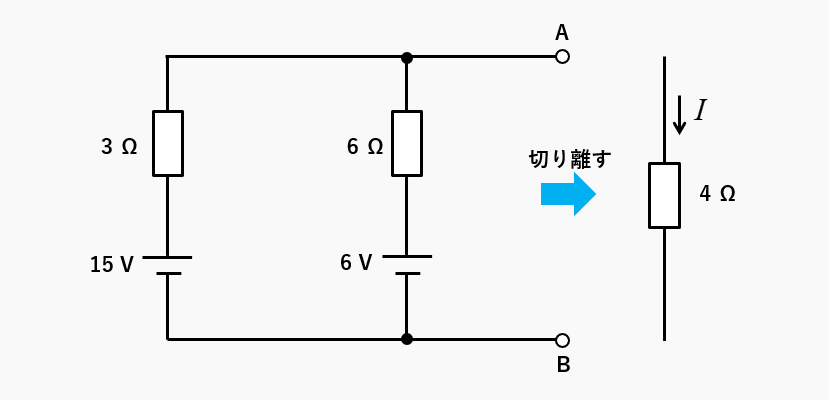
手順2(等価電源を求める)
等価電源 \(V_0\) を求める
端子AB間の電圧が、等価電源になります。等価電源を求めるには、回路に流れる電流を求める必要があります。
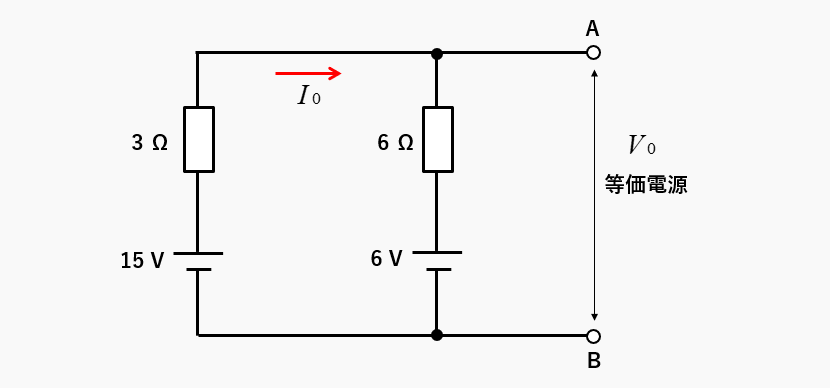
回路に流れる電流 \(I_0\) は、オームの法則から
\(I_0=\cfrac{\rm電圧}{\rm抵抗}=\cfrac{15-6}{3+6}=1\) [A]
回路に流れる電流が分かりましたので、端子AB間の電圧は、次の2つの方法で求められます。
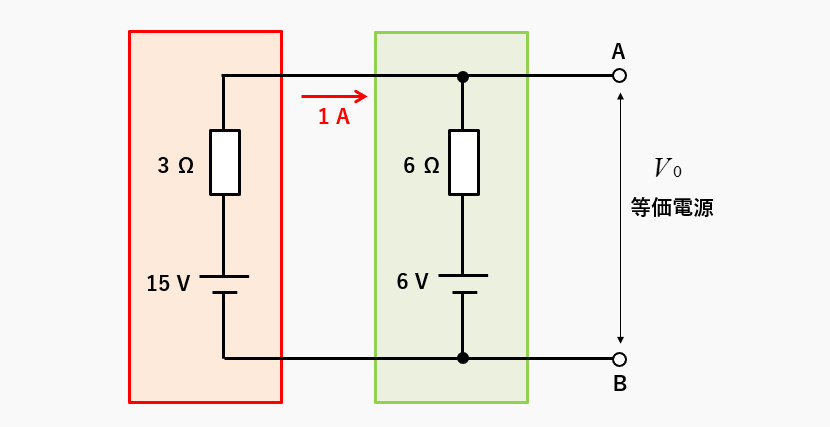
左側の回路で、端子AB間の電圧を求めると
15V-(3Ω✕1A)=12V
右側の回路で、端子AB間の電圧を求めると、6V+(6Ω✕1A)=12V になり、どちらも同じになります。
等価電源 \(V_0=12\) [V] になります。
閉回路の端子電圧を求める場合、起電力と電圧降下のプラス・マイナスについて知ることが大切です。
起電力のプラス・マイナスと電圧降下の正負と閉回路の向き
手順3(等価抵抗を求める)
等価抵抗 \(R_0\) を求める
端子AB間の抵抗が、等価抵抗になります。等価抵抗を求めるには、電圧源の電源なので回路内の電源を短絡します。
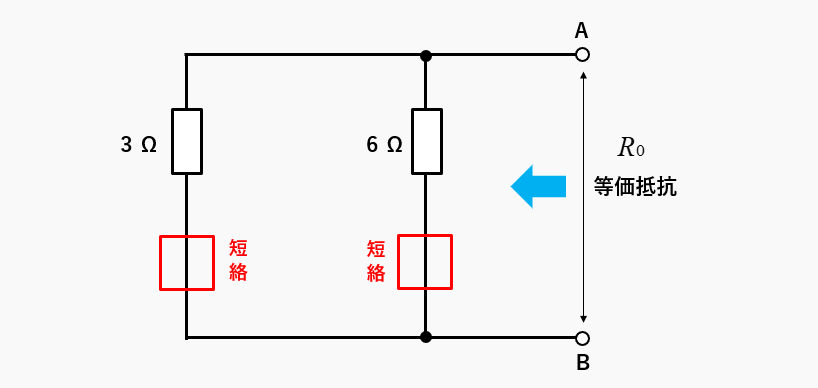
端子ABから見た抵抗は、3Ωと6Ω の並列接続です。和分の積を使って計算します。
等価抵抗 \(R_0=\cfrac{3×6}{3+6}=2\) [Ω]
手順4(等価回路に変換する)
テブナンの定理
\(I=\cfrac{V_0}{R_0+R}\)
- \(V_0\)・・・等価電源
- \(R_0\)・・・等価抵抗
- \(R\)・・・負荷抵抗
等価電源と等価抵抗が求められたので、元の回路を等価回路に変換します。
等価電源 \(V_0=12\) [V]
等価抵抗 \(R_0=\cfrac{3×6}{3+6}=2\) [Ω]
求める電流は、4Ω の抵抗に流れる電流です。等価回路の回路図を見れば分かる通り、抵抗の直列回路なのでオームの法則で求めることができます。
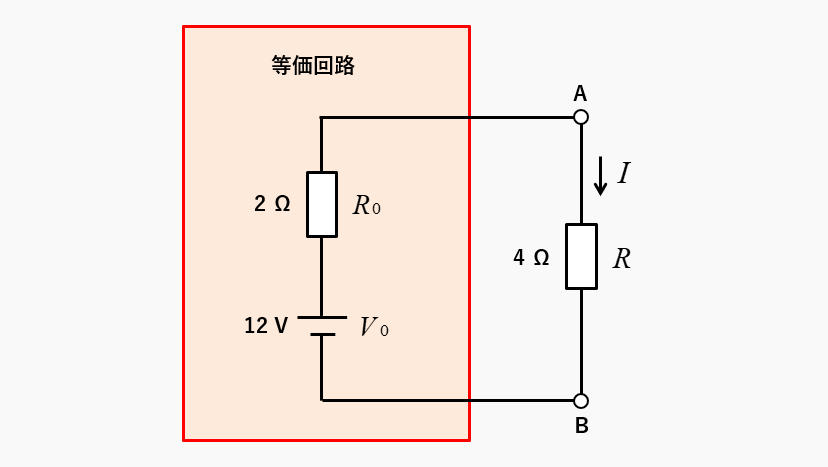
求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}\)\(=\cfrac{12}{2+4}=2\) [A]
テブナンの定理の使い方(電流源)
テブナンの定理
\(I=\cfrac{V_0}{R_0+R}\)
- \(V_0\)・・・等価電源
- \(R_0\)・・・等価抵抗
- \(R\)・・・負荷抵抗
電流源の例題
図のような電流源の回路を例にして、3Ωの抵抗に流れる電流を「テブナンの定理」で求めます。
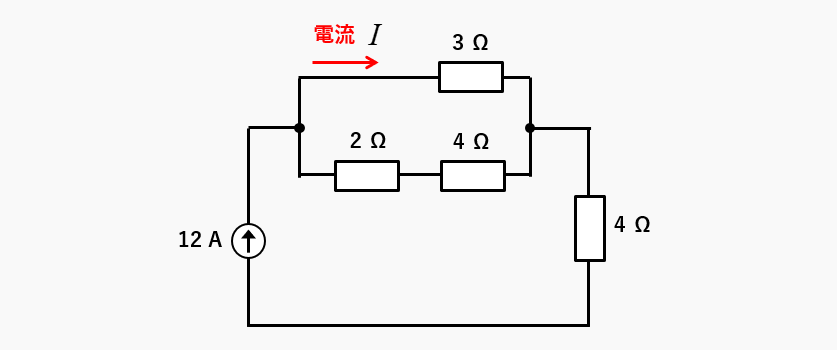
手順1(抵抗を切り離す)
図のように、3Ωの抵抗を切り離します。
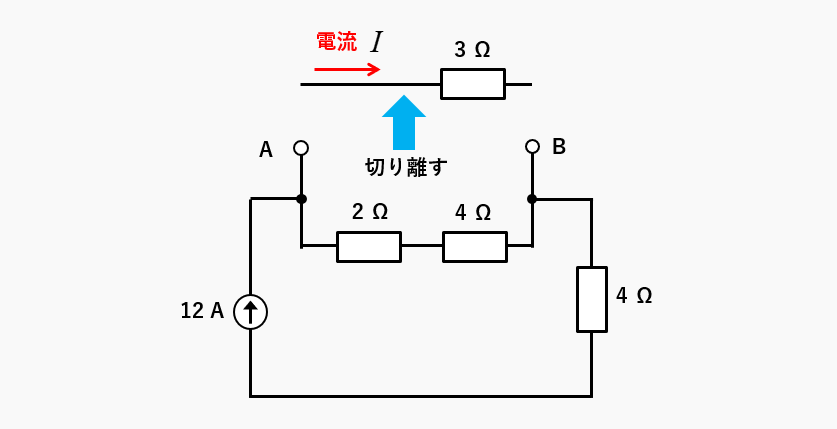
手順2(等価電源を求める)
等価電源 \(V_0\) を求める。
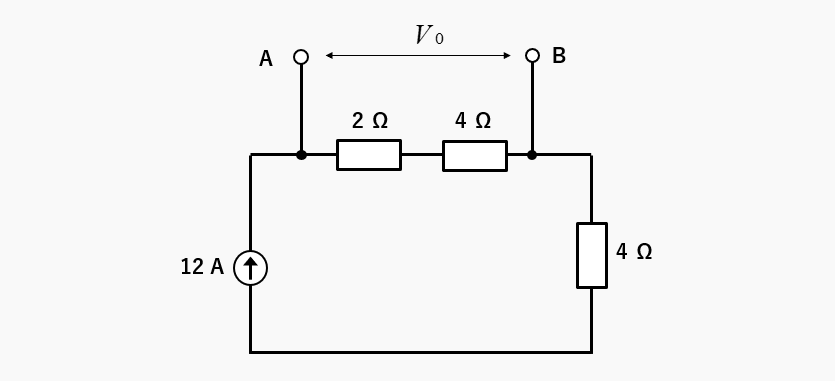
端子AB間の電圧が、等価電源になります。端子AB間の電圧は、電圧降下と等しくなります。オームの法則から 12A✕(2Ω+4Ω)=72V
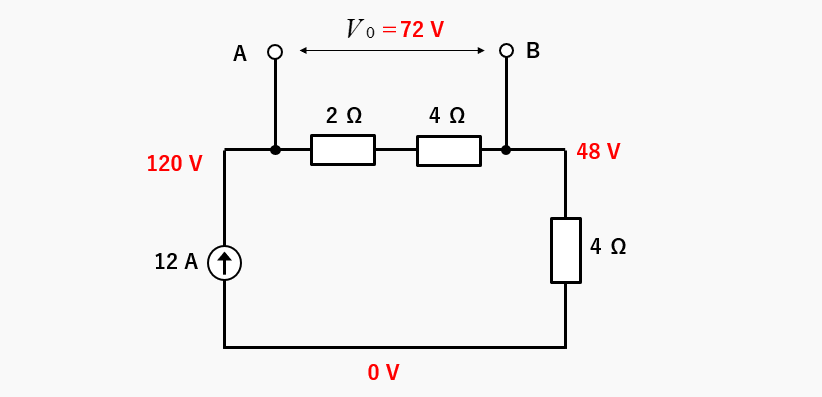
等価電源は \(V_0=72\) [V] になります。
手順3(等価抵抗を求める)
等価抵抗 \(R_0\) を求める
端子AB間の抵抗が、等価抵抗になります。等価抵抗を求めるには、図のように回路内の電流源を開放します。
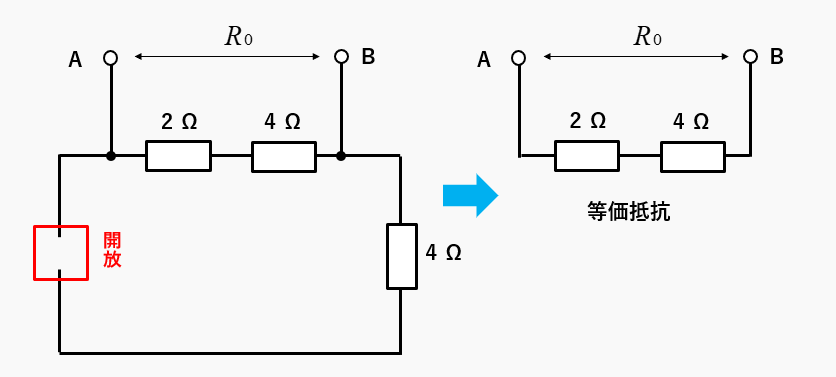
電流源を開放したので、端子ABから見た抵抗は、2Ωと4Ωの直列接続です。直列接続の抵抗は、足せばよいので6Ωになります。
等価抵抗 \(R_0=6\) [Ω]
手順4(等価回路に変換する)
テブナンの定理
\(I=\cfrac{V_0}{R_0+R}\)
- \(V_0\)・・・等価電源
- \(R_0\)・・・等価抵抗
- \(R\)・・・負荷抵抗
等価電源と等価抵抗が求められたので、元の回路を等価回路に変換します。
等価電源 \(V_0=72\) [V]
等価抵抗 \(R_0=6\) [Ω]
求める電流は、3Ωの抵抗に流れる電流です。等価回路の回路図を見れば分かる通り、抵抗の直列回路なのでオームの法則で求めることができます。
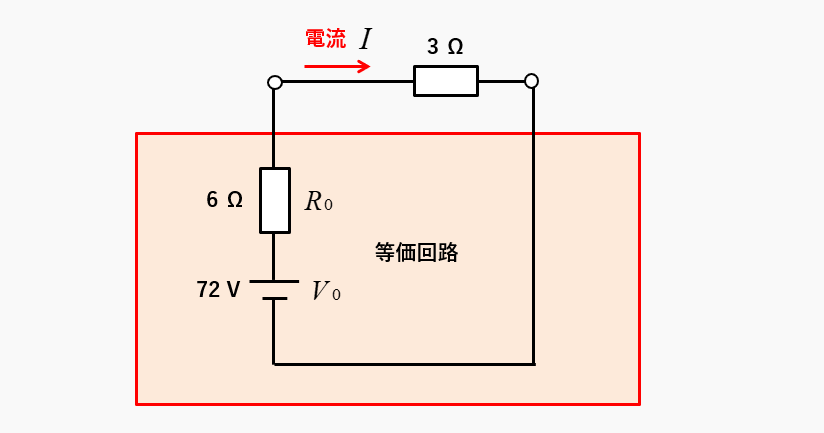
求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}\)\(=\cfrac{72}{6+3}=8\) [A] になります。
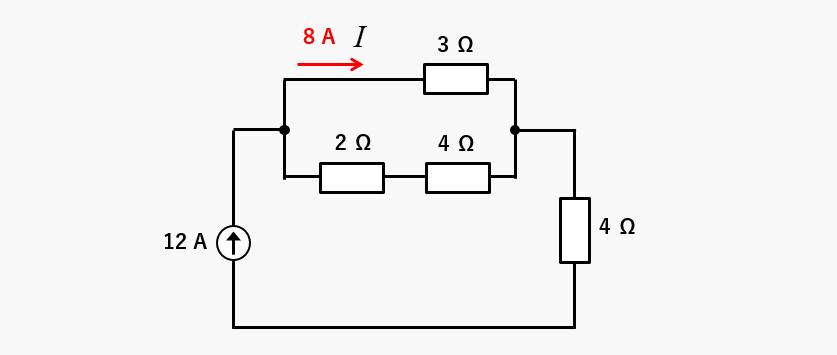
2Ωと4Ωの直列接続に流れる電流
2Ωと4Ωの直列接続に流れる電流は、12A-8A=4A になります。
\(\cfrac{2}{6}×12=4\) [A]
テブナンの定理でブリッジ回路を解く
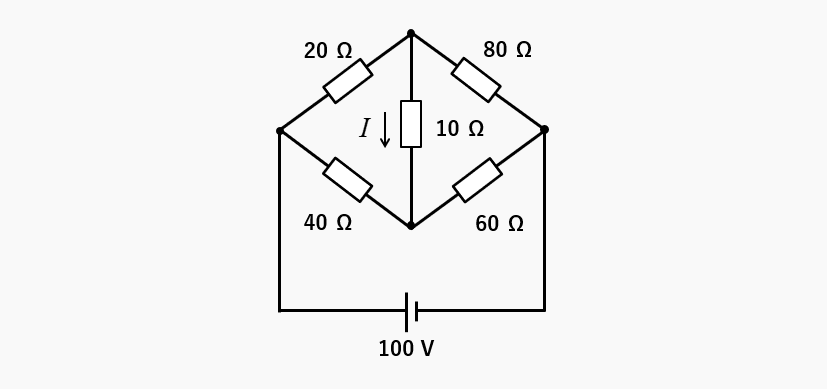
図のようなブリッジ回路の電流 \(I\) [A] を、テブナンの定理で求める場合、等価電源 \(V_0\) を、電位から求めることができます。
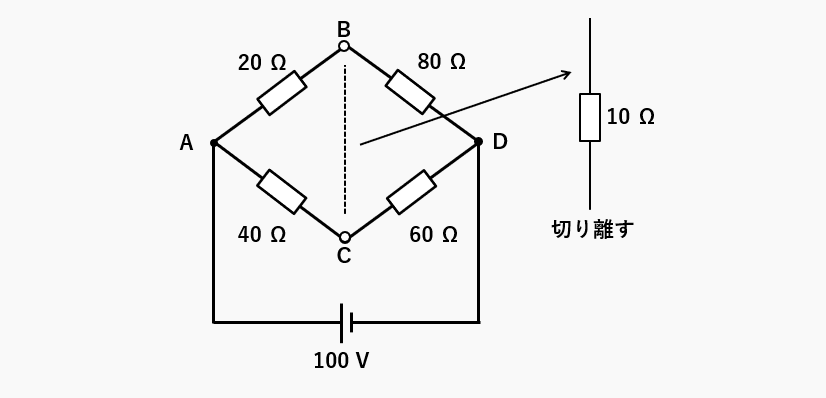
手順1(等価電源を求める)
10Ωの抵抗を切り離し、それぞれの端子をABCDとします。
手順2(等価電源を求める)
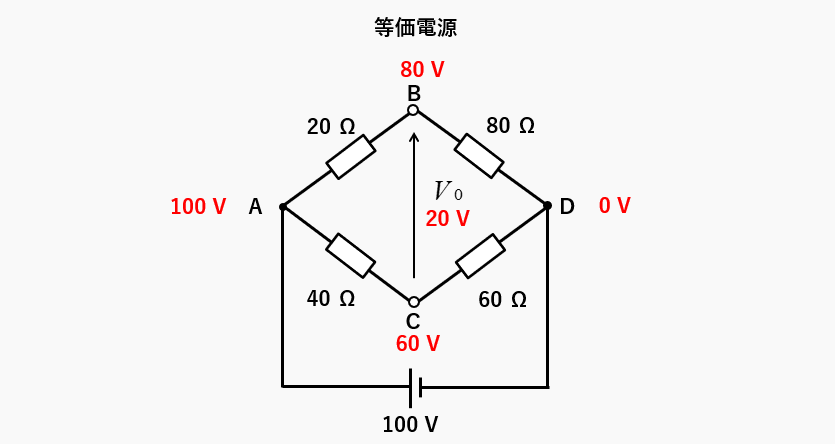
等価電源 \(V_0\) を求める。電源のマイナスを基準として、0Vとします。各端子の電位は次のようになります。
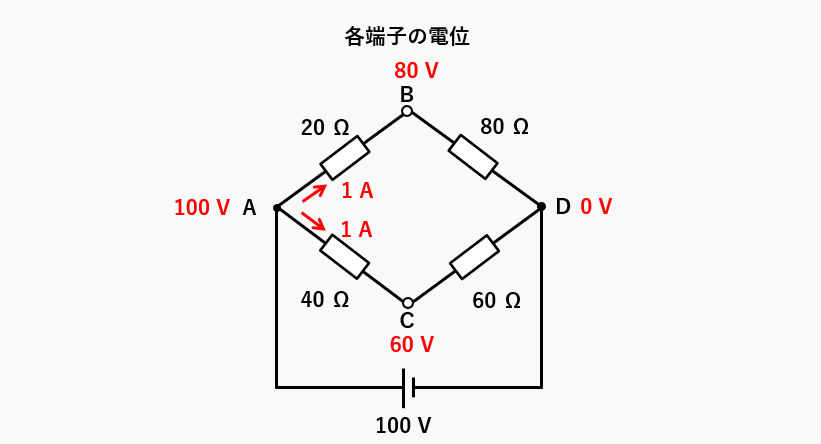
- A\(\cdots100\) [V]
- B\(\cdots100-20=80\) [V]
- C\(\cdots100-40=60\) [V]
- D\(\cdots 0\) [V]
等価電源 \(V_0=V_{BC}\) は、Bの電位 80V、Cの電位 60V から
等価電源 \(V_0=80-60=20\) [V] になります。
手順3(等価抵抗を求める)
等価抵抗は、端子BCから見た時の抵抗になります。等価抵抗を求めるために、回路内の電源を短絡し整理すると、2つの並列抵抗が「直列接続」になっています。
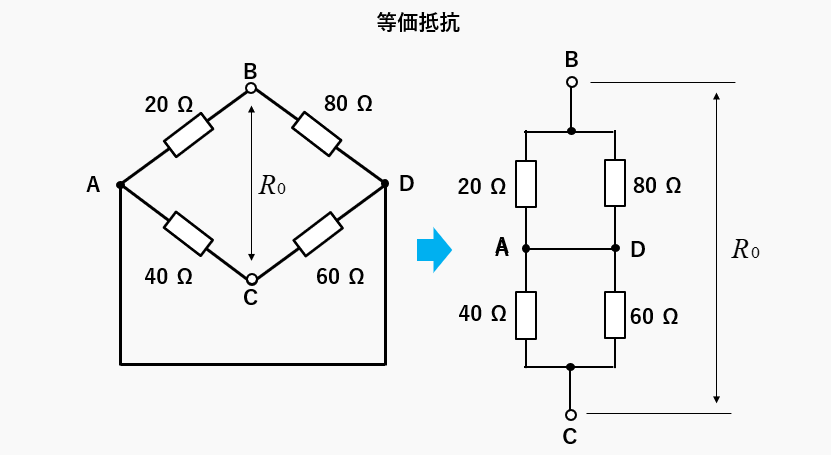
等価抵抗 \(R_0\) は、BCから見た合成抵抗になります。
等価抵抗 \(R_0=\cfrac{20×80}{20+80}+\cfrac{40×60}{40+60}=40\) [Ω] となります。
テブナンの定理で等価回路に変換する
テブナンの定理
\(I=\cfrac{V_0}{R_0+R}\)
- \(V_0\)・・・等価電源
- \(R_0\)・・・等価抵抗
- \(R\)・・・負荷抵抗
等価電源 \(V_0=80-60=20\) [V]
等価抵抗 \(R_0=\cfrac{20×80}{20+80}+\cfrac{40×60}{40+60}=40\) [Ω]
元の回路を等価電源と等価抵抗で等価回路に変換します。
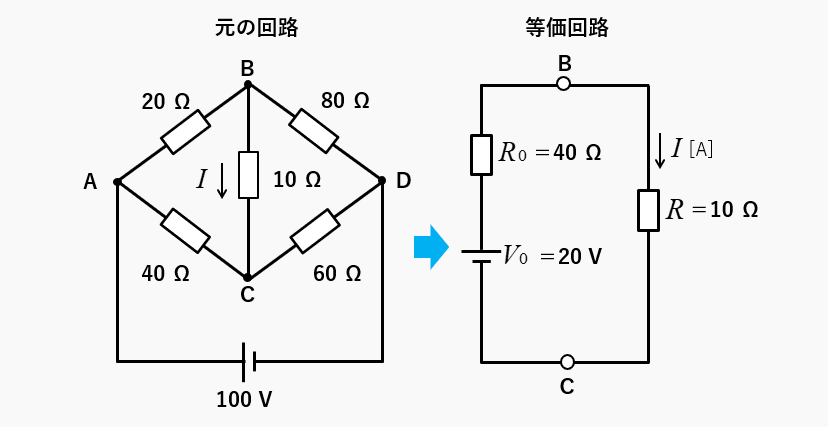
\(R\) [Ω] に流れる電流 \(I\) [A] は、次のようになります。
\(I=\cfrac{V_0}{R_0+R}=\cfrac{20}{40+10}=0.4\) [A]
テブナンの定理を検証する
テブナンの定理で解析した時の、元の回路と等価回路の電圧や電流の値の違いについて検証します。
次の回路の例題を解いて検証をします。4Ωの抵抗に流れる電流 \(I\) をテブナンの定理で求めます。
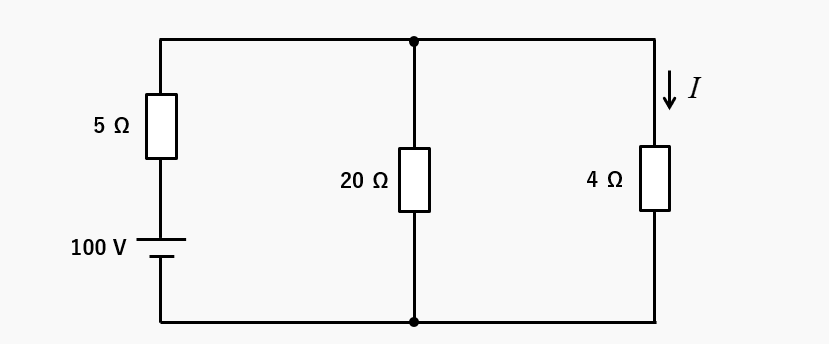
等価電源を求める
4Ωの抵抗を回路から切り離して、等価電源を求めます。
等価電源の値は、20Ωの端子電圧になります。等価電源は、回路内を流れる電流 \(I_0\) が分かれば求められます。
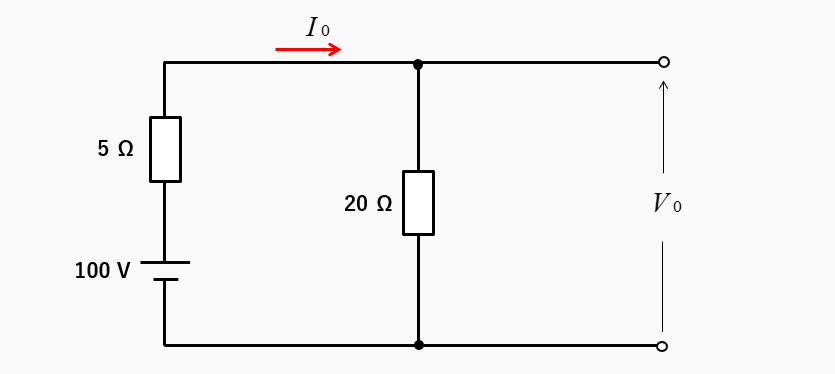
\(I_0=\cfrac{100}{25}=4\) [A] から
\(V_0=100-5×4=80\) [V]
等価抵抗を求める
テブナンの定理により、電源を短絡します。等価抵抗は、5Ωと20Ωの並列接続です。
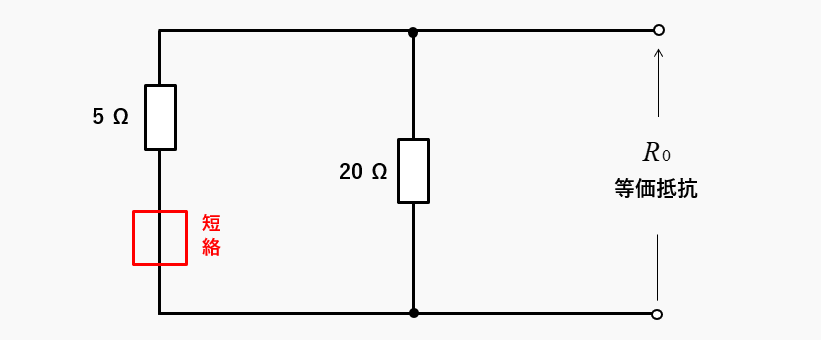
抵抗の並列接続なので、和分の積で求めます。
等価抵抗 \(R_0=\cfrac{5×20}{5+20}=4\) [Ω]
テブナンの定理で等価回路に変換する
等価電源 \(V_0=100-5×4=80\) [V]
等価抵抗 \(R_0=\cfrac{5×20}{5+20}=4\) [Ω]
元の回路を等価回路にすると、次のようになります。
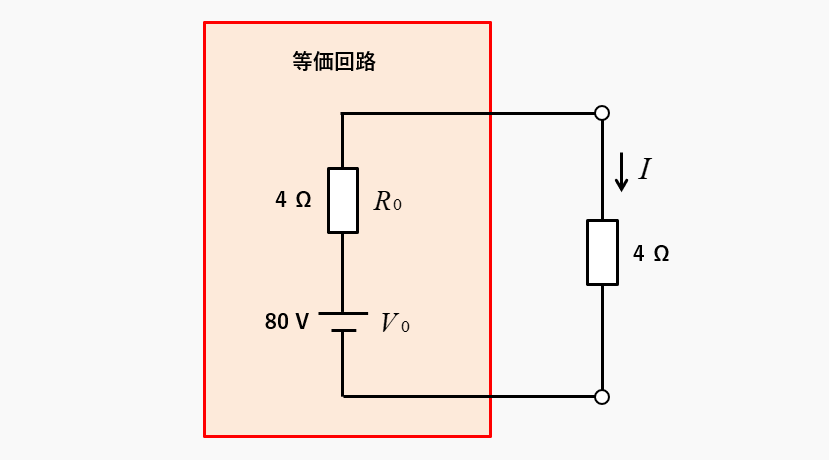
求める電流 \(I\) は
\(I=\cfrac{80}{8}=10\) [A] になります。
テブナンの定理の各要素の検証
等価回路の各要素の値は、次の図のようになります。
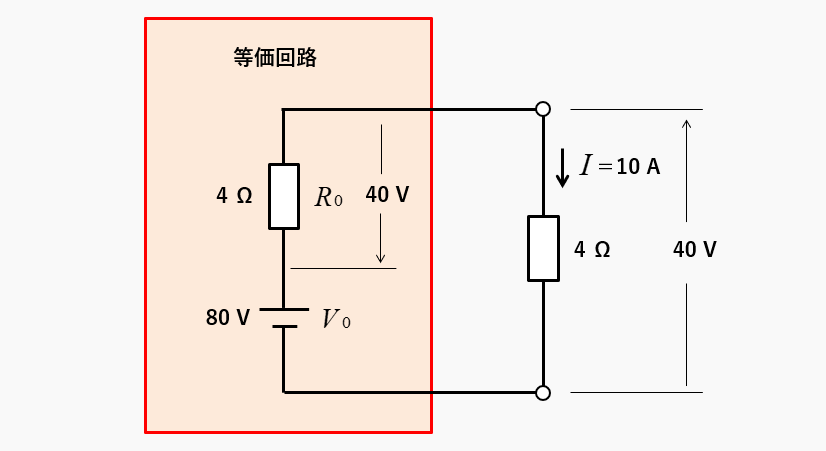
等価電源の値は、\(V_0=80\) [V]、等価抵抗の値は、\(R_0=4\) [Ω]、等価抵抗 \(R_0=4\) の電圧降下は40V、負荷4Ωの抵抗の電圧降下は40V、流れる電流は10Aになります。
元の回路の各要素の値は、次のようになります。
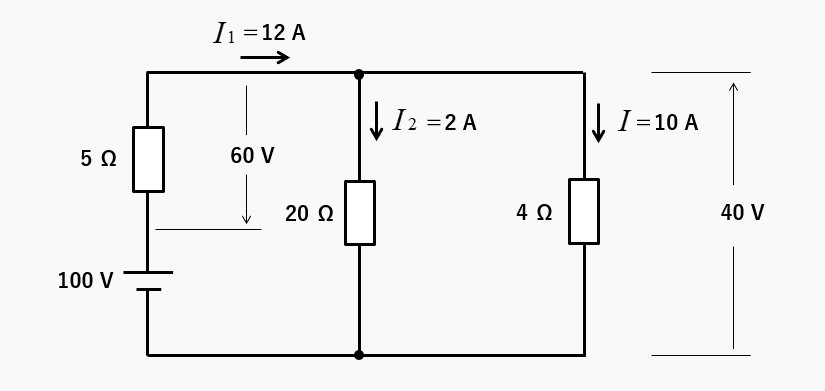
回路の合成抵抗は
\(R=5+\cfrac{20×4}{20+4}=\cfrac{25}{3}\) [Ω]
回路全体を流れる電流 \(I_1\) は
\(I_1=\cfrac{100}{\cfrac{25}{3}}=12\) [A]
4Ωに流れる電流 \(I\) は
\(I=\cfrac{40}{4}=10\) [A]
回路全体を流れる電流は、\(I_1=I+I_2\) の関係があります。
\(I_2=I_1-I=12-10=2\) [A]
\(I_2=I_1×\cfrac{4}{20+4}=2\) [A]
4Ωと20Ωの抵抗に掛かる電圧は40V
5Ωの抵抗に掛かる電圧は60Vになります。
まとめ
テブナンの定理のまとめ
- 電流を求めたい部分を切り離します。
- 等価電源 \(V_0\) を求めます。
- 等価抵抗 \(R_0\) を求めます。
(回路内部の電圧源はすべて短絡して除去します。)
(回路内部の電流源はすべて開放して除去します。) - 等価回路に変換します。
- 目的の電流 \(I=\cfrac{V_0}{R_0+R}\) [A] を求めます。
以上で「テブナンの定理の使い方【任意の場所に流れる電流を求める定理】」の説明を終わります。