電気回路の計算をするときは、起電力や電圧降下の正負を考える必要があります。
起電力は電圧と電流の向きが同じですが、電圧降下は電圧と電流の向きが逆になります。
起電力は電源なので、それ自体が電気(電圧)を作れます。それに対し、電圧降下は電流が流れることで、発生する電圧(電位差)です。
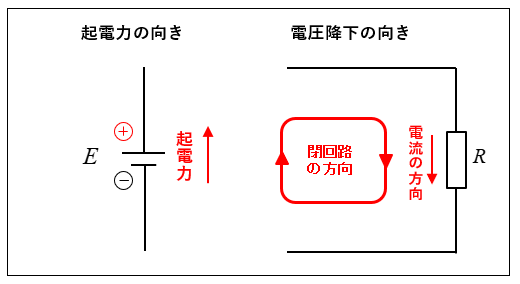
起電力の正負 プラスとマイナスの決め方

起電力は電源のことで、それ自体で電気を作ることができます。つまり、回路が繋がっていなくても、電源の両端には電圧があります。
電圧が高い方をプラスとし、電圧が低い方をマイナスとします。起電力の向きは、低い方から高い方になります。
電流の向きは、電圧の高い方から低い方へ流れますので、起電力の向きと同じ向きになります。
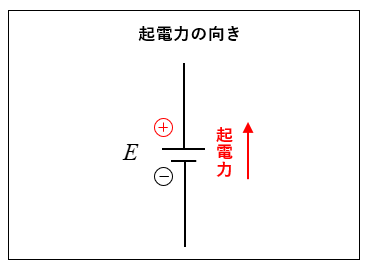
電圧・電流・電圧降下の矢印表現をリンク
矢印の始点から終点(先)に向かって電圧は高くなります。
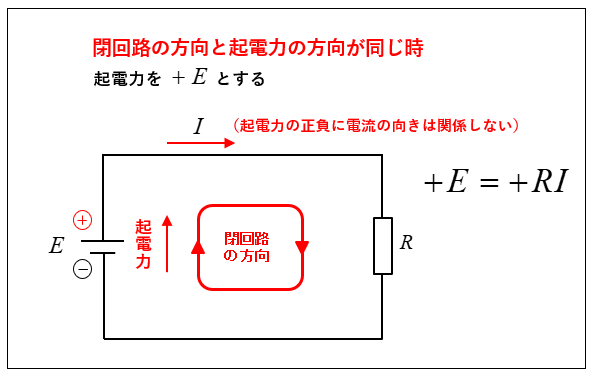
起電力の正(プラス)の決め方
閉回路の方向と起電力の方向が「同じ場合」、その起電力を正(プラス)とします。ただし、流れる電流の向きは、起電力の正負と関係ありません。
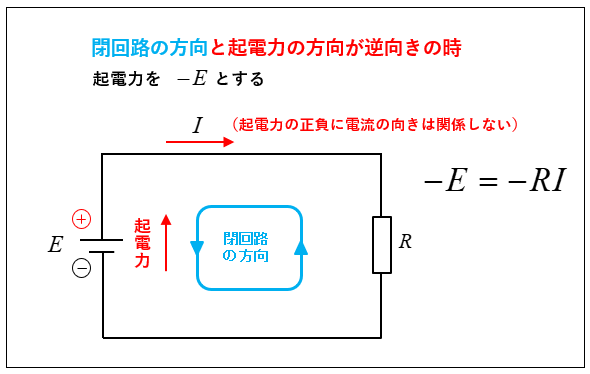
起電力の負(マイナス)の決め方
閉回路の方向と起電力の方向が「逆向きの場合」、その起電力を負(マイナス)とします。ただし、流れる電流の向きは、起電力の正負と関係ありません。
電気回路の閉回路の向きの決め方
閉回路の向きは右向きでも左向きでも、自分の好きなように決めて構いません。一般的には、起電力の方向に決める方が、問題を解きやすくなります。
次のような回路について、閉回路の向きを考えてみます。
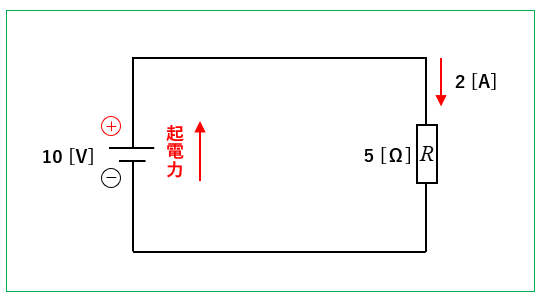
■ 閉回路1
図のように、閉回路の向きを右向きにした場合
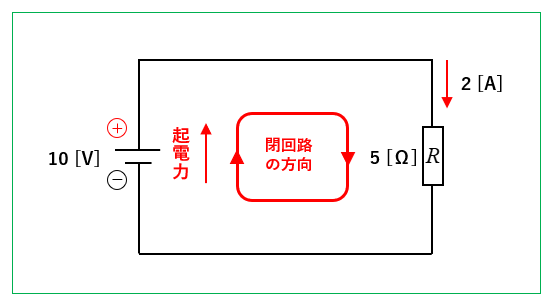
キルヒホッフの第2法則から起電力の和は電圧降下の和と等しいので
起電力の和は \(10\) [V]
電圧降下の和は \(2×5=10\) [V] なので
\(10=2×5\) [V] になります。
■ 閉回路2
図のように閉回路の向きを左向きにした場合

キルヒホッフの第2法則から起電力の和は電圧降下の和と等しいので
起電力の和は \(-10\) [V]
電圧降下の和は \(-(2×5)=-10\) [V] なので\(-10=-(2×5)\) [V] になります。
両辺のマイナス符号を取れば、右向きの閉回路と同じ結果になります。つまり、どの向きに閉回路をとっても良いということです。
電圧降下の正負 プラス(+)とマイナス(-)の決め方
電圧降下の向き
電圧降下の向きは、電流が流れ込む方向が正(プラス)になります。

電圧降下の正(プラス)
閉回路の方向と電流の流れる方向が「同じ場合」、その電圧降下を正(プラス)とします。電圧降下は図のように、仮想の電池を考えるとわかりやすくなります。
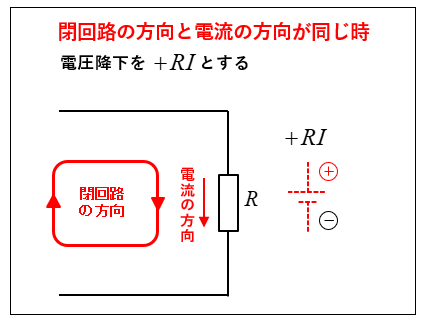
電圧降下の負(マイナス)
閉回路の方向と電流の流れる方向が「異なる場合」、その電圧降下を負(マイナス)とします。電圧降下は図のように、仮想の電池を考えるとわかりやすくなります。
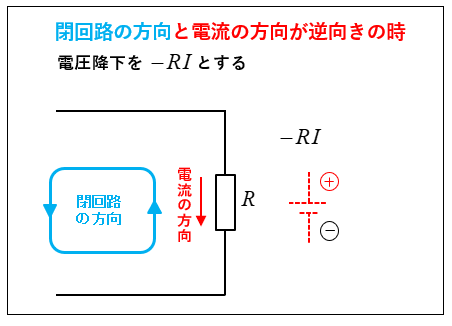
起電力と電圧降下の例
回路に流れる電流の向きと閉回路の向きを、図のように仮定して起電力と電圧降下の例を示します。
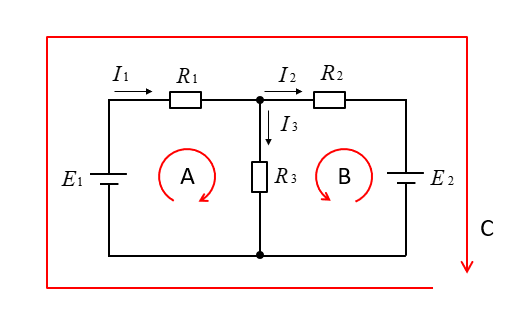
■ 閉回路Aの場合の正負
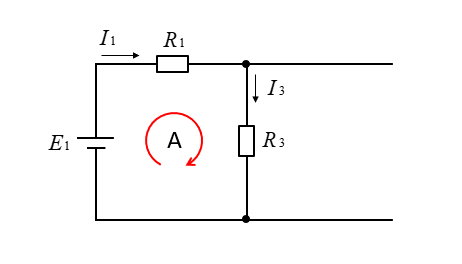
- \(E_1\) は閉回路の向きと起電力の向きが同じなので \(+E_1\) になります。
- \(R_1\) の電圧降下は閉回路の向きと電流の向きが同じなので \(+R_1I_1\) になります。
- \(R_3\) の電圧降下は閉回路の向きと電流の向きが同じなので \(+R_3I_3\) になります。
\(E_1=R_1I_1+R_3I_3\) が成立します。
■ 閉回路Bの場合の正負
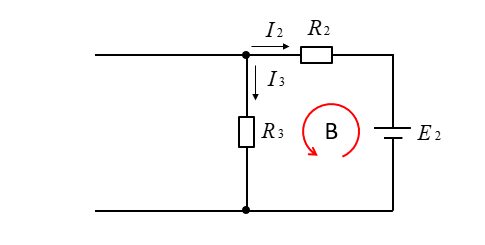
- \(E_2\) は閉回路の向きと起電力の向きが同じなので \(+E_2\) になります。
- \(R_2\) の電圧降下は閉回路の向きと電流の向きが逆なので \(-R_2I_2\) になります。
- \(R_3\) の電圧降下は閉回路の向きと電流の向きが同じなので \(+R_3I_3\) になります。
\(E_2=-R_2I_2+R_3I_3\) が成立します。
■ 閉回路Cの場合の正負
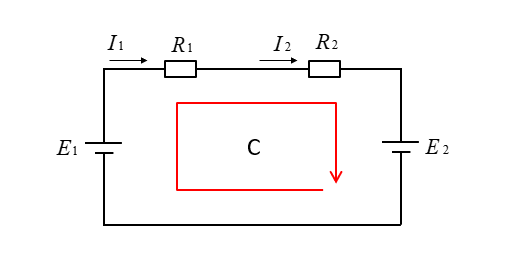
- \(E_1\) は閉回路の向きと起電力の向きが同じなので \(+E_1\) になります。
- \(E_2\) は閉回路の向きと起電力の向きが逆なので \(-E_2\) になります。
- \(R_1\) の電圧降下は閉回路の向きと電流の向きが同じなので \(+R_1I_1\) になります。
- \(R_2\) の電圧降下は閉回路の向きと電流の向きが同じので \(+R_2I_2\) になります。
\(E_1-E_2=R_1I_1+R_2I_2\) が成立します。
練習問題
問題1
次の回路の各抵抗に流れる電流を求めよ。
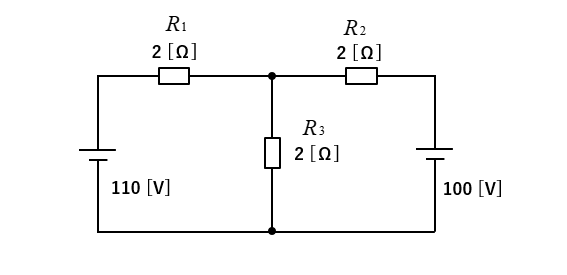
<解答例>
各抵抗に流れる電流と向きを自分で仮定して構いませんので、次のように仮定します。
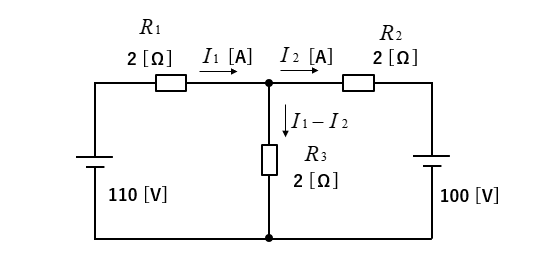
\(R_3\) に流れる電流を \(I_3\) としても良いのですが、未知数はできるだけ少なくしたほうが計算が楽になります。
閉回路Aを計算します。
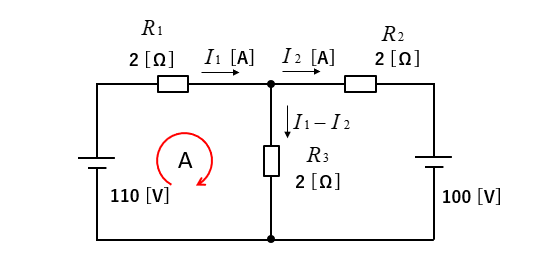
\(110=2I_1+2(I_1-I_2)=4I_1-2I_2\)
\(110=4I_1-2I_2\cdots(1)\)
次に閉回路Bを計算します。
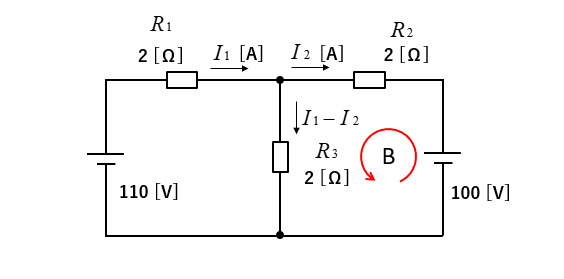
\(100=-2I_2+2(I_1-I_2)=2I_1-4I_2\)
\(100=2I_1-4I_2\cdots(2)\)
式(1)の両辺を2倍します。
\(220=8I_1-4I_2\cdots(3)\)
式(3)の両辺と式(2)の両辺を引き算します。
\(220-100=8I_1-2I_1\)
\(6I_1=120\) から
\(I_1=20\) [A]
式(2)に \(I_1\) の値を代入すると
\(100=2×20-4I_2\) から
\(I_2=-15\) [A] ですから、仮定した向きと逆の向きに流れることになります。
各抵抗の電流の値と向きを示すと、次のようになります。
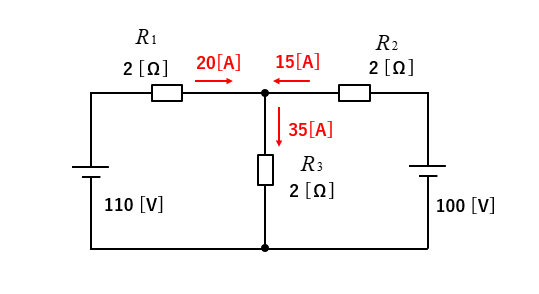
問題2
次のような回路で抵抗 \(R_3\) に流れる電流がわかっている時、抵抗 \(R_3\) の値と両端に掛かる電圧を求めよ。
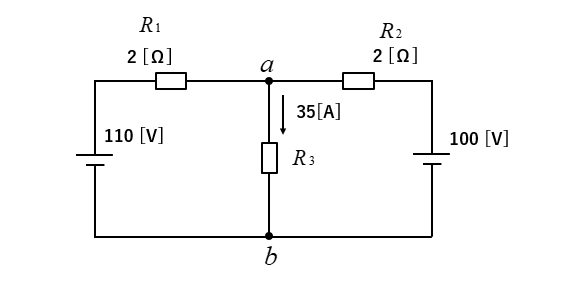
<解答例>
電圧降下で考える。回路に流れる電流を、図のように仮定します。\(R_2\) に流れる電流 \(I_2\) を \(I_1\) を使って表します。
\(I_1+I_2=35\) から \(I_2=35-I_1\) になります。
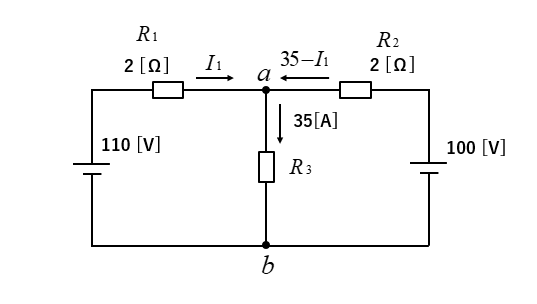
\(R_1\) と \(R_2\) の電圧降下が電源の電圧の差になります。
\(110-100=2I_1-2(35-I_1)\)
\(4I_1=80\)
\(I_1=20\) [A]
\(I_2=15\) [A]
各抵抗での電圧降下は、図のようになります。
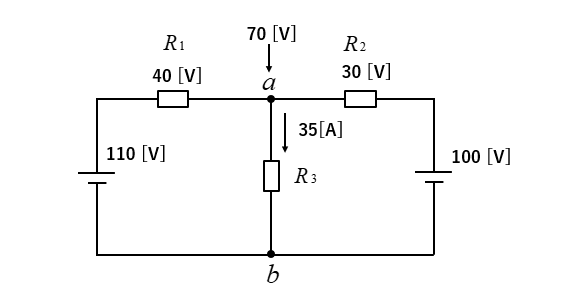
\(a\) の電圧は、左側の電源から見ると
\(110-40=70\) [V]
右側の電源から見ると
\(100-30=70\) [V] で同じになります。
抵抗 \(R_3\) の値は
\(R_3=\cfrac{70}{35}=2\) [Ω] になります。