三相交流は起電力の位相を120度ずらした、3つの交流を組み合わせた交流です。
三相電力は、位相の異なる3つの単相電力を組み合わせたものになります。
三相交流の結線にはスター結線とデルタ結線がありますが、線間電圧と線電流で表すと三相電力の公式は、\(\sqrt3\)✕線間電圧✕線電流✕力率となります。
この記事では、三相電力の公式となぜ、\(\sqrt3\)が付くのか?について説明します。
三相電力の公式

三相電力の公式は、\(\sqrt3\)✕線間電圧✕線電流✕力率 です。
三相電力の公式
三相電力=\(\sqrt3\) × 線間電圧 × 線電流 × 力率 [W]
\(P=\sqrt{3}V_lI_l\cosθ\) [W]
三相電力を \(P\) [W]
線間電圧を \(V_l\) [V]
線電流を \(I_l\) [A]
力率を \(\cosθ\)
三相交流の結線方式は、スター結線とデルタ結線がありますが、線間電圧と線電流を使うと結線方式に関係なく三相電力の公式を使うことができます。
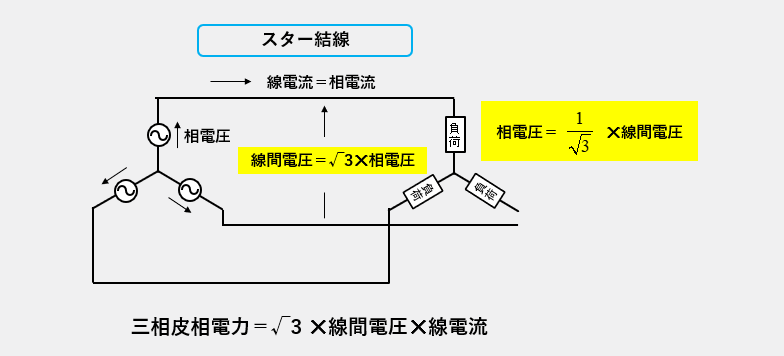
スター結線の三相電力の公式
スター結線は
- 線間電圧=\(\sqrt3\) 相電圧
相電圧=\(\cfrac{1}{\sqrt3}\) 線間電圧 の関係です。 - 線電流=相電流
三相電力=\(\sqrt3\) 線間電圧✕線電流になります。
デルタ結線の三相電力の公式
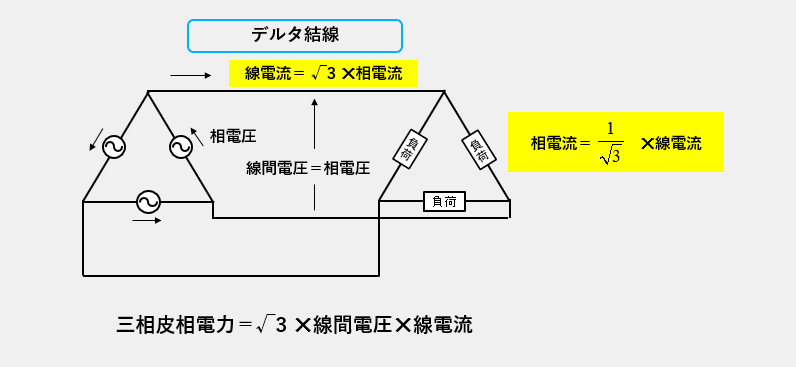
デルタ結線は
- 線間電圧=相電圧
- 線電流=\(\sqrt3\)相電流
相電流=\(\cfrac{1}{\sqrt3}\) 線電流 の関係です。
三相電力=\(\sqrt3\) 線間電圧✕線電流になります。
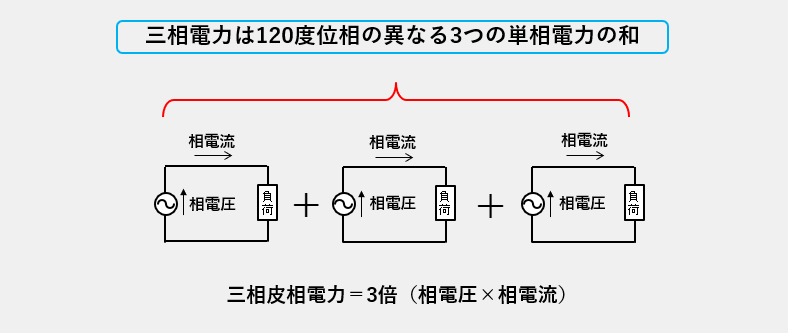
三相電力は「3つの単相電力の和」
三相電力は、120度位相の異なる「3つの単相電力の和」になるので、力率を除いた三相皮相電力は、三相皮相電力=3倍✕単相電力になります。
三相電力の公式は、スター結線、デルタ結線に関係なく使うことができる
三相電力の公式
三相電力=\(\sqrt3\) × 線間電圧 × 線電流 × 力率 [W]
\(P=\sqrt{3}V_lI_l\cosθ\) [W]
三相電力を \(P\) [W]
線間電圧を \(V_l\) [V]
線電流を \(I_l\) [A]
力率を \(\cosθ\)
スター結線に三相電力の公式が使える理由
スター結線は
相電圧=\(\cfrac{1}{\sqrt3}\)線間電圧
相電流=線電流 の関係があります。
スター結線の三相交流電力を、上記の「単相電力の3倍」の式に代入します。
三相電力=3✕相電圧✕相電流✕力率=3✕\(\cfrac{1}{\sqrt3}\)線間電圧✕線電流✕力率 なので
三相電力=\(\sqrt3\)✕線間電圧✕線電流✕力率 になります。
デルタ結線に三相電力の公式が使える理由
デルタ結線は
相電圧=線間電圧
相電流=\(\cfrac{1}{\sqrt3}\)線電流 の関係があります。
デルタ結線の三相交流電力を、上記の「単相電力の3倍」の式に代入します。
三相電力=3✕相電圧✕相電流✕力率=3✕線間電圧✕\(\cfrac{1}{\sqrt3}\)線電流✕力率 なので
三相電力=\(\sqrt3\)✕線間電圧✕線電流✕力率 になります。
三相電力の公式に√3が付く理由
三相電力の公式に、\(\sqrt3\) が付く理由をスター結線で説明します。
スター結線で、三相電力の公式に \(\sqrt3\) が付くのは、次の図のように、線間電圧 \(=\sqrt3×\) 相電圧 の関係があるためです。
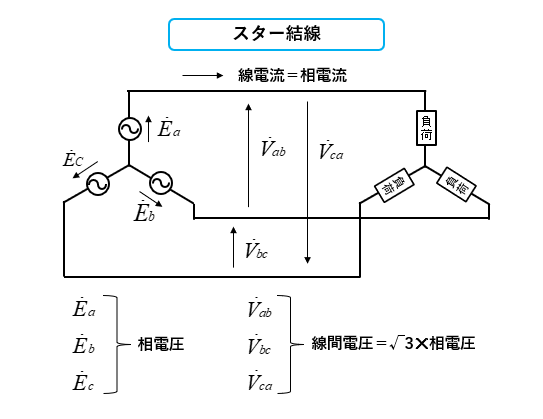
スター結線の相電圧と線間電圧の関係
相電圧と線間電圧の関係を、式で表すと次のとおりです。
\(V_{ab}=E_a-E_b\)
\(V_{bc}=E_b-E_c\)
\(V_{ca}=E_c-E_a\)
スター結線の相電圧と線間電圧のベクトル図
ベクトル図から、線間電圧が相電圧の \(\sqrt3\) 倍になることを求めます。
スター結線の線間電圧は、\(V_{ab}=E_a-E_b\)、\(-E_b\) は、\(E_b\) を反転したものです。
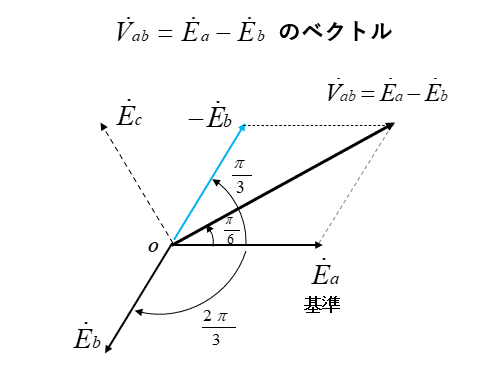
ベクトル図から線間電圧を求める
次の図のように、線間電圧 \(V_{ab}\) は、\(E_a\) と \(-E_b\) のベクトルを合成したものです。
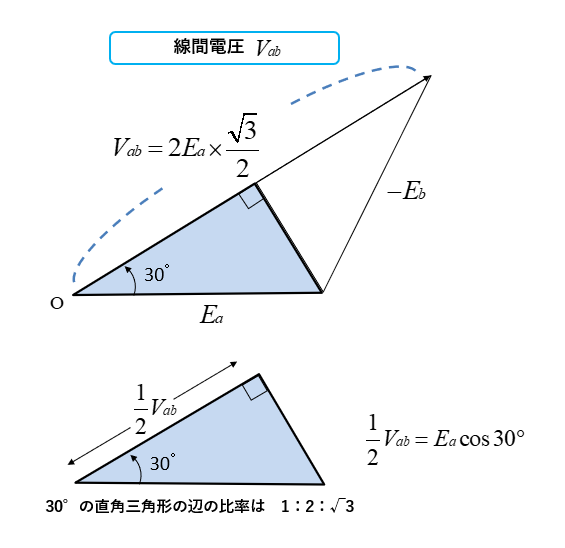
1辺が30°の直角三角形の辺の比率は、1:2:√3 ですから、\(\cfrac{1}{2}V_{ab}=E_a\cos30°\)
\(V_{ab}=2×E_a\cos30°=2×E_a×\cfrac{\sqrt3}{2}=\sqrt3×E_a\)
したがって、線間電圧は、相電圧の \(\sqrt3\) 倍になります。
線間電圧=\(\sqrt3\)✕相電圧
相電圧=\(\cfrac{1}{\sqrt3}\)✕線間電圧
線間電圧の位相は、相電圧より30°進みます。
スター結線の線電流と相電流の関係は、線電流=相電流です。
以上のことから、三相電力の公式は、
三相電力=3✕相電圧✕線電流✕力率
三相電力=3✕(線間電圧✕\(\cfrac{1}{\sqrt3}\))✕線電流✕力率
三相電力=\(\sqrt3\) × 線間電圧 × 線電流 × \(\cosθ\) [W] になります。
三相電力の公式のまとめ
三相電力の公式は、\(\sqrt3\)✕線間電圧✕線電流✕力率 で求めます。
三相電力の公式
三相電力=\(\sqrt3\) × 線間電圧 × 線電流 × 力率 [W]
\(P=\sqrt{3}V_lI_l\cosθ\) [W]
三相電力を \(P\) [W]
線間電圧を \(V_l\) [V]
線電流を \(I_l\) [A]
力率を \(\cosθ\)
三相電力の公式は、スター結線、デルタ結線の結線方式に関係なく使うことができます。