合成抵抗の計算は、電気回路の計算をする場合の基本になります。
複雑に見える合成抵抗でも、基本的には「抵抗の直列接続と並列接続」の組み合わせです。
合成抵抗の公式は、直列接続の公式・並列接続の公式・和分の積の公式があります。
合成抵抗を計算する場合には、少しコツが必要になります。
- 単純に合成できる抵抗から計算する
- 2つの直列接続の抵抗から計算する
- 2つの並列接続の抵抗から計算する
この記事では、合成抵抗を計算する場合の公式と合成する場合のコツを解説します。
直列接続の公式
\(R_0=R_1+R_2+R_3+\cdots+R_n\) [Ω]
並列接続の公式
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cdots+\cfrac{1}{R_n}\) [Ω]
和分の積(2個の抵抗の並列接続)
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
2個の抵抗の並列接続のときだけ、和分の積の公式が使えます。
和分の積
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
合成抵抗の公式

合成抵抗の公式は、直列接続の公式・並列接続の公式・和分の積の公式があります。
直列接続の公式
\(R_0=R_1+R_2+R_3+\cdots+R_n\) [Ω]
並列接続の公式
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cdots+\cfrac{1}{R_n}\) [Ω]
和分の積(2個の抵抗の並列接続)
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
直列接続の合成抵抗の公式
図のように \(n\) 個 の抵抗が直列接続になっている回路があります。
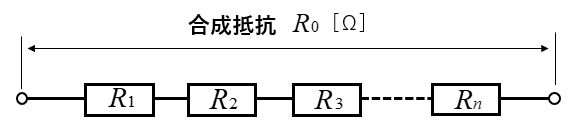
この回路の合成抵抗 \(R_0\) を求める公式は、次のようになります。
直列接続の公式
\(R_0=R_1+R_2+R_3+\cdots+R_n\) [Ω]
直列接続の合成抵抗の求め方は、2個でも3個でもそれ以上でも、それぞれの抵抗の値を足し算をすれば求めることができます。
直列接続の合成抵抗が足し算になるわけ
直列接続の合成抵抗が単純に、足し算になるわけは次のように考えることができます。抵抗の数がいくつあっても同じように考えることができますので、2つの抵抗の直列接続を考えます。
直列接続の抵抗回路では、回路に流れる電流 \(I\) が同じ大きさになります。
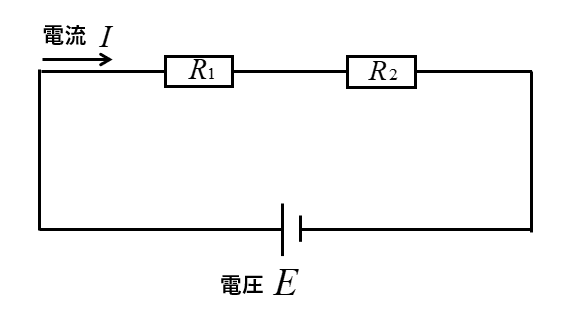
抵抗 \(R_1\) の電圧降下はオームの法則から \(R_1I\) 、同じように抵抗 \(R_2\) の電圧降下は \(R_2I\) になります。
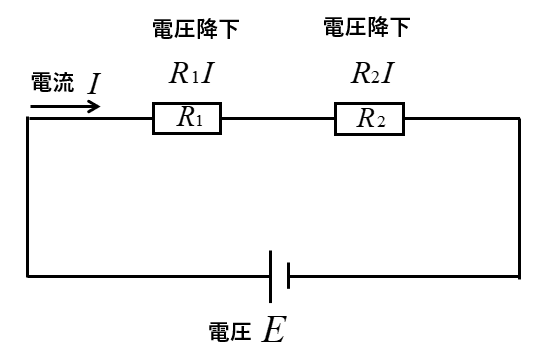
合成抵抗を \(R_0\) とすると、電源電圧は \(R_0I\) となります。
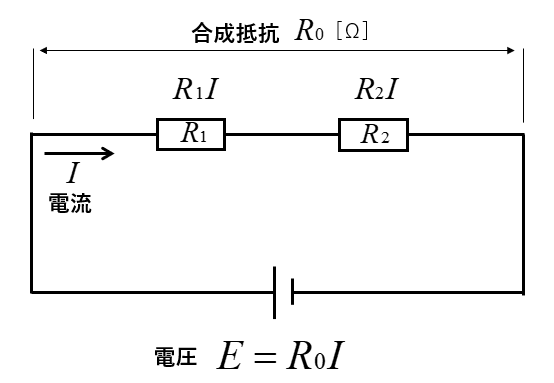
キルヒホッフの法則から、電源電圧=電圧降下の和 が成り立ちます。
\(R_0I=R_1I+R_2I\) から \(I\) を取り除くと
\(R_0=R_1+R_2\) になり、各抵抗の足し算になることがわかります。
2個以上の抵抗の場合でも、同じことになります。
並列接続の合成抵抗の公式
図のように \(n\) 個 の抵抗が並列接続になっている回路があります。
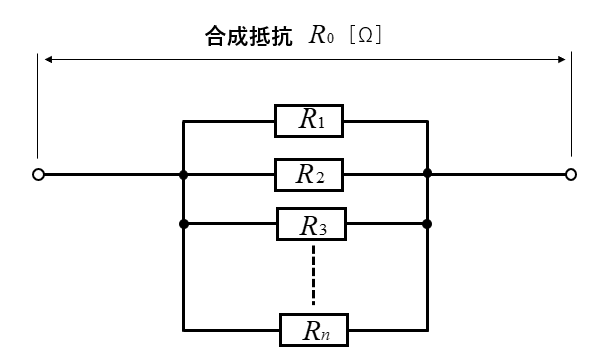
この回路の合成抵抗 \(R_0\) を求める公式は、次のようになります。
並列接続の公式
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cdots+\cfrac{1}{R_n}\) [Ω]
上の公式は、合成抵抗の逆数になっていますので、合成抵抗を求めるには、\(R_0=\) の形に直す必要があります。
並列接続の合成抵抗の逆数が各抵抗の逆数の和になるわけ
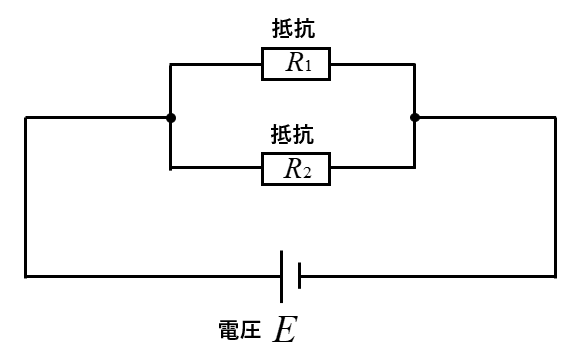
並列接続の合成抵抗の逆数が各抵抗の逆数の和になるわけは、次のように考えることができます。抵抗の数がいくつあっても同じように考えることができますので、2つの抵抗の直列接続を考えます。
並列接続の抵抗回路では、各抵抗に同じ大きさの電圧 \(E\) がかかります。
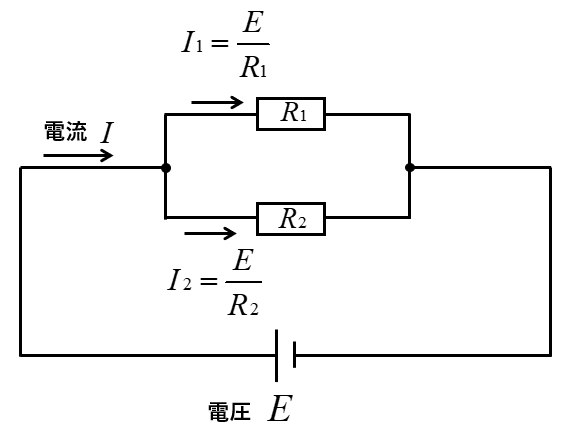
抵抗 \(R_1\) に流れる電流はオームの法則から \(\cfrac{E}{R_1}\) 、同じように抵抗 \(R_2\) に流れる電流は \(\cfrac{E}{R_2}\) になります。
回路に流れる電流は \(\cfrac{E}{R_0}\) となります。
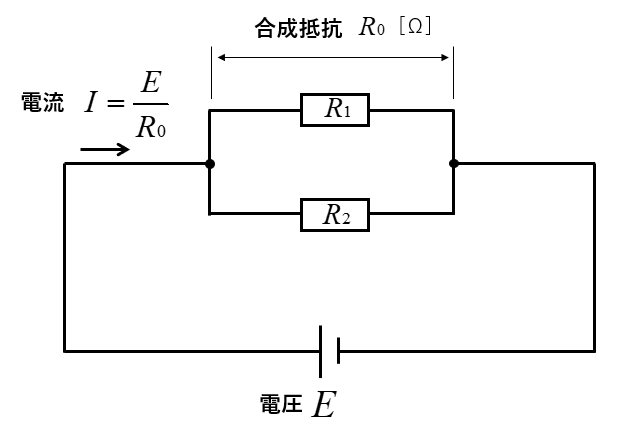
キルヒホッフの法則から、回路に流れる電流=各抵抗に流れる電流の和 が成り立ちます。
\(I=I_1+I_2\)
\(\cfrac{E}{R_0}=\cfrac{E}{R_1}+\cfrac{E}{R_2}\) から \(E\) を取り除くと
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\) になり、並列接続の公式が求められます。
和分の積の公式(2個の抵抗が並列接続のときに使える公式)
並列回路において、2個の抵抗が並列接続のときだけ、「和分の積の公式」が使えます。
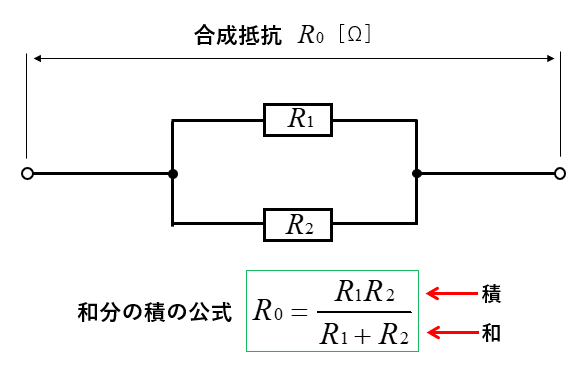
和分の積の公式
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
上図のように、2個の抵抗が、並列に接続されているときの合成抵抗は、「和分の積の公式」を使うことができる。
【重要】
■「和分の積」の公式は、2個のときだけしか使えない。
■ 並列接続の合成抵抗は、元のそれぞれの抵抗の値より、必ず小さい値になります。
和分の積の公式の求め方
和分の積の公式は、並列接続の公式から求められます。
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\) を変形して
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\)
コンダクタンスについて
抵抗の逆数は、コンダクタンスになります。
コンダクタンスは \(G\) で表し、記号に [S] ジーメンス を使います。
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}+\cdots+\cfrac{1}{R_n}\) [Ω]
合成コンダクタンスを \(G_0\) で表すと
\(G_0=G_1+G_2+G_3+\cdots+G_n\) [S] となります。
直列接続の合成抵抗の計算例
直列接続の計算例を示します。直列接続の合成抵抗は、単純に「足せば良い」ので簡単です。
計算例1
図のように、30Ωと15Ωの抵抗が、直列に接続されています。合成抵抗 \(R_0\) を求めよ。

直列接続の合成抵抗は、抵抗を足せば良いので
\(R_0=30+15=45\) [Ω] になります。
計算例2
図のように、10Ωと8Ωと9Ωの抵抗が、直列に接続されています。合成抵抗 \(R_0\) を求めよ。

直列接続の合成抵抗は、いくつあっても、それぞれの抵抗を足せば良いので
\(R_0=10+8+9=27\) [Ω] になります。
並列接続の合成抵抗の求め方
並列接続の計算例を示します。2個の抵抗が並列接続のときは、「和分の積の公式」を使うと簡単に計算できます。
和分の積の公式
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
2個の抵抗が並列接続の合成抵抗の計算例1
図のように、30Ωと20Ωの抵抗が、並列に接続されています。合成抵抗 \(R_0\) を求めよ。
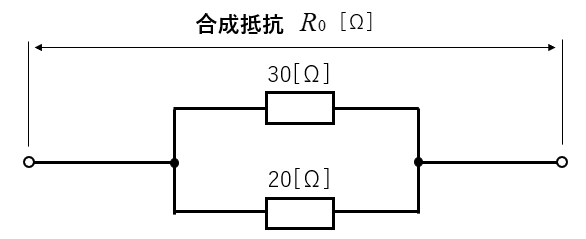
2個の抵抗の並列接続の合成抵抗は、「和分の積」を使います。
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) の式に代入して
\(R_0=\cfrac{30×20}{30+20}=\cfrac{600}{50}=12\) [Ω]
2個の抵抗が並列接続の合成抵抗の計算例2
図のように、50Ωと50Ωの抵抗が、並列に接続されています。合成抵抗 \(R_0\) を求めよ。
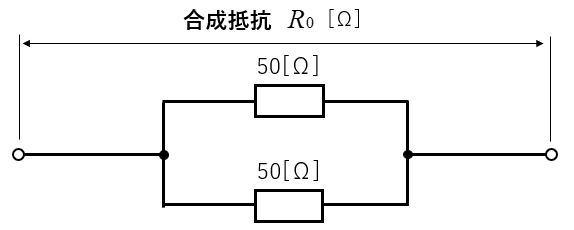
2つの抵抗の並列接続の合成抵抗は、和分の積が使えます。
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) に代入して
\(R_0=\cfrac{50×50}{50+50}=\cfrac{2500}{100}=25\) [Ω] になります。
並列回路の抵抗が同じ値のときの合成抵抗の特徴
抵抗が同じ値のときの、並列接続の合成抵抗は、次のような特徴があります。
【重要】
並列に接続する抵抗が「同じ値」のときは、抵抗値を抵抗の数で割れば 合成抵抗 になります。
■ \(30\) [Ω] の抵抗を2個並列にした場合は
\(R_0=\cfrac{30}{2}=15\) [Ω] となります。
■ 同様に \(30\) [Ω] を3個並列に接続した場合は
\(R_0=\cfrac{30}{3}=10\) [Ω] となります。
3個以上でも有効です。
3個の抵抗が並列接続の合成抵抗の計算例
3個の抵抗が並列接続の、合成抵抗の求め方は2つの方法があります。
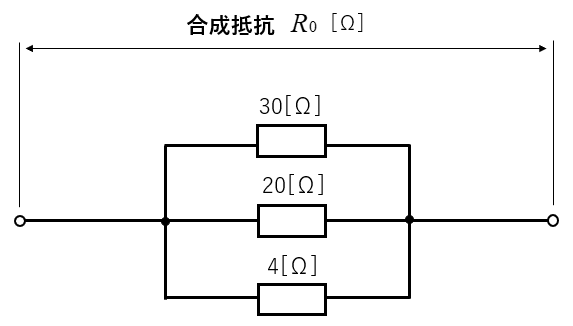
- 和分の積を2回使う方法
- 並列接続の合成抵抗の公式を使う方法
和分の積を2回使う方法
和分の積の公式の1回目
3個の抵抗30Ω、20Ω、4Ωのうちの、どれか2個の抵抗を選んで「和分の積の公式」を使います。
計算しやすそうな、30Ωと20Ωの抵抗で「和分の積の公式」を使います。
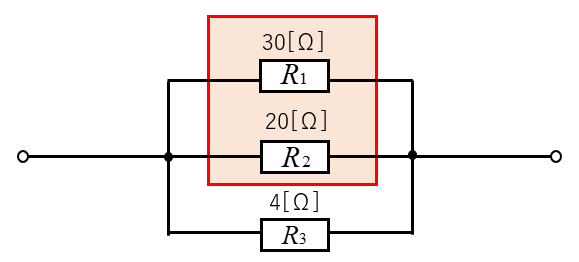
30Ωと20Ωの合成抵抗を \(R\) とすると、「和分の積の公式」に代入して
\(R=\cfrac{20×30}{20+30}=12\) [Ω]
元の回路は、次の回路と同じになります。
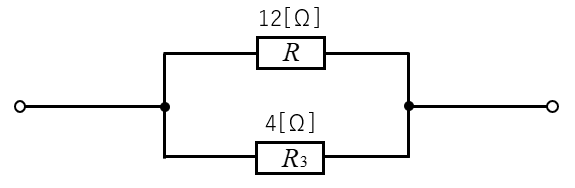
上の回路に和分の積の公式を、代入すると
\(R_0=\cfrac{12×4}{12+4}=\cfrac{48}{16}=3\) [Ω] になります。
並列接続の公式による計算例

3個の抵抗の値を「並列接続の公式」に代入します。
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}\) の公式から
\(\cfrac{1}{R_0}=\cfrac{1}{30}+\cfrac{1}{20}+\cfrac{1}{4}\)
\(\cfrac{1}{R_0}=\cfrac{2}{60}+\cfrac{3}{60}+\cfrac{15}{60}\)
\(\cfrac{1}{R_0}=\cfrac{20}{60}=\cfrac{1}{3}\)
合成抵抗 \(R_0=\) の形に変形すると
\(R_0=3\) [Ω]
直列接続と並列接続が混同した回路の合成抵抗の計算例
直列接続と並列接続が混ざっている、抵抗の回路を「直並列接続」と呼びます。
直並列接続の回路の、合成抵抗を求めるのは複雑そうに見えます。しかし、基本的には簡単にできるものから、合成抵抗を求めていけば良いので実際はそれほど難しくはありません。
直並列接続の合成抵抗の計算例
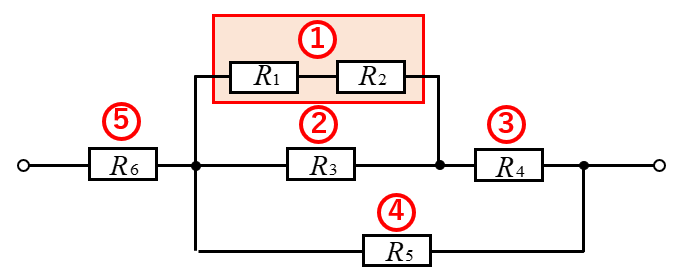
計算例1
図のような、直並列接続の回路があります。一見とても難しそうに見えます。しかし、「チョットしたコツ」をわかっていれば、簡単に合成抵抗を求められます。
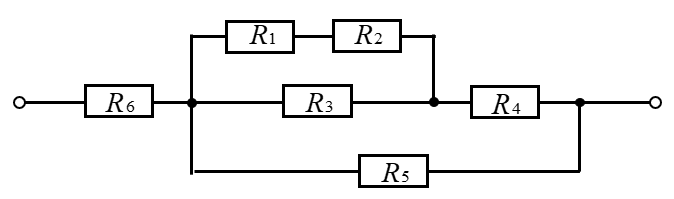
直並列接続のコツは、簡単に合成できるものから合成するということ。
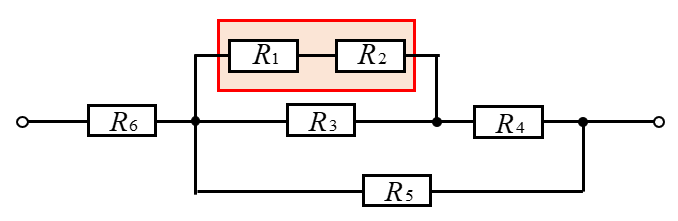
ここの例では、\(R_1\) と \(R_2\) の直列接続の合成抵抗を求めることから始めます。
上図の合成の順序を説明します。
- \(R_1\) と \(R_2\) の直列接続を合成
- 1 の結果と \(R_3\) で並列接続を合成
- 2 結果と \(R_4\) で直列接続を合成
- 3 の結果と \(R_5\) で並列接続を合成
- 4 結果と \(R_6\) で直列接続を合成
計算例2
同じような例ですが、もう1つ解説します。
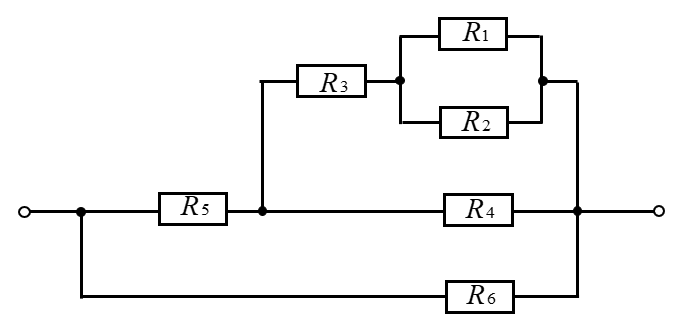
直並列接続のコツは、簡単に合成できるものから合成するということ。
上図の合成の順序を説明します。
- \(R_1\) と \(R_2\) の並列接続を合成
- 1 の結果と \(R_3\) で直列接続を合成
- 2 結果と \(R_4\) で並列接続を合成
- 3 の結果と \(R_5\) で直列接続を合成
- 4 結果と \(R_6\) で並列接続を合成
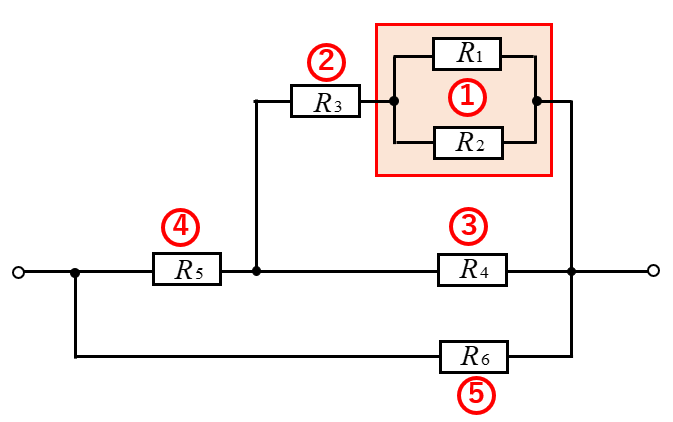
上の例で分かるように、直列でも並列でも、合成しやすいものから合成していけば良いということになります。
まとめ
合成抵抗の求め方の公式は、「直列接続の公式」と「並列接続の公式」と「和分の積の公式」があります。
直列接続の公式
\(R_0=R_1+R_2+R_3+\cdots+R_n\) [Ω]
並列接続の公式
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cdots+\cfrac{1}{R_n}\) [Ω]
和分の積(2個の抵抗の並列接続)
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
2個の抵抗の並列接続のときだけ、和分の積の公式が使えます。
和分の積の公式
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
【分圧の法則】抵抗による電圧の分圧
【分流の法則】抵抗による電流の分流
【初心者向け】並列回路の電圧・電流・抵抗の関係をわかりやすく解説!