和分の積（わぶんのせき）は、並列接続された2つの抵抗の 合成抵抗を求める公式 です。
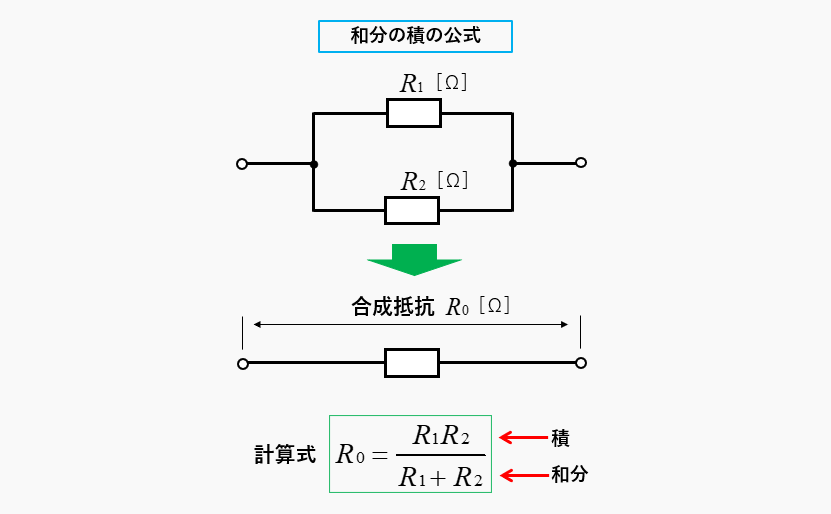
\(R_1\) と \(R_2\) の抵抗が並列に接続されています。
合成抵抗を \(R_0\) とすると、和分の積の公式により
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) で求めることができます。
和分の積の公式の使い方と、並列接続された抵抗値が同じ場合の使い方について説明します。
和分の積の公式
和分の積の公式
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\)
和分の積の公式の求め方
和分の積の公式は、並列接続の合成抵抗の公式から求められます。
合成抵抗を \(R_0\) とすると、並列接続の合成抵抗の公式は
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\)
式を整理すると
\(\cfrac{1}{R_0}=\cfrac{R_2+R_1}{R_1R_2}\)
式を \(R_0=\) に変形すると
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) となり
「和分の積」の公式を求めることができます。
和分の積の公式の使い方
和分の積は、抵抗の並列接続を合成するときに便利な公式です。
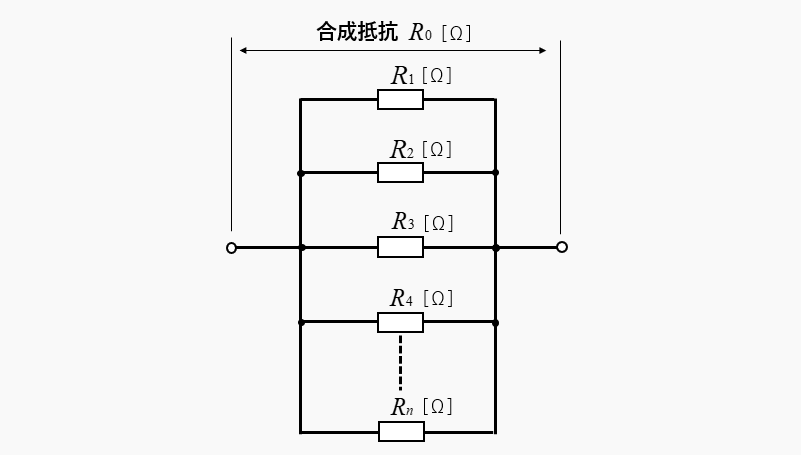
- 複数の抵抗が並列接続されている場合
-
任意の2つの抵抗を「和分の積」で、１つの合成抵抗に変換する。
「どの抵抗」と「どの抵抗」を組み合わせて、和分の積を使っても大丈夫です。
\(R_2\) と \(R_4\)
\(R_1\) と \(R_3\)
\(R_3\) と \(R_4\) など
計算し易い、抵抗の組み合わせを選ぶことが重要です。
- 和分の積を繰り返す
-
和分の積を繰り返して使うことで、合成抵抗 \(R_0\) を求められます。
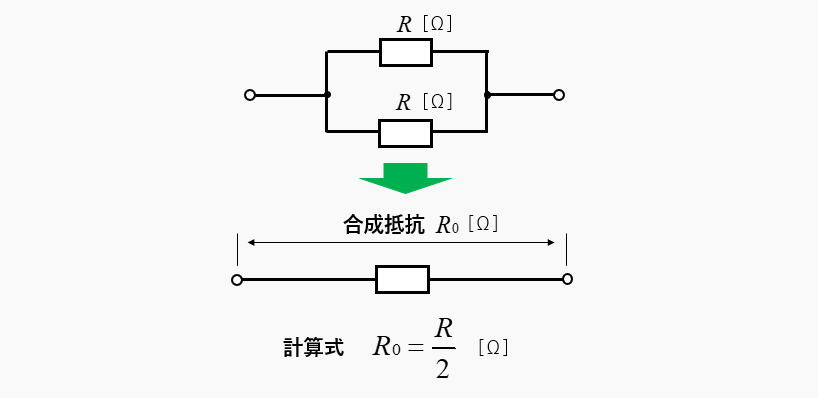
並列接続された2つの抵抗値が同じ場合の合成抵抗は1/2になる
2つの並列接続の 抵抗値が同じ 場合の合成抵抗
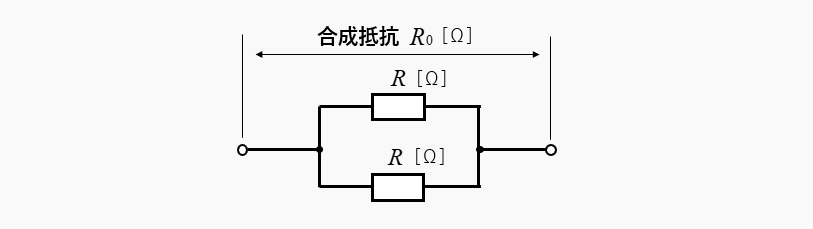
- ２つの抵抗値が同じ場合
-
合成抵抗 \(R_0=\cfrac{R}{2}\) [Ω]
１つの抵抗値の \(\cfrac{1}{2}\) になります。
並列接続された、2つの抵抗値が同じ場合の合成抵抗は、１つの抵抗値の \(\cfrac{1}{2}\) になります。
1/2になることを和分の積の公式から求める
１つの抵抗値の \(\cfrac{1}{2}\) になる理由を、和分の積の公式から求める。
和分の積の公式
\(R_0=\cfrac{R1R_2}{R_1+R_2}\)
2つの抵抗の値が同じ場合
\(R_1、R_2=R\) とすると
和分の積の公式から
\(R_0=\cfrac{RR}{R+R}=\cfrac{R^2}{2R}\)
\(R_0=\cfrac{R}{2}\)
１つの抵抗値の \(\cfrac{1}{2}\) になります。
1/2になることを並列接続の合成抵抗の公式から求める
１つの抵抗値の \(\cfrac{1}{2}\) になる理由を、並列接続の合成抵抗の公式から求める。
並列接続の合成抵抗の公式
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\)
2つの抵抗値が同じ場合は
\(R_1、R_2=R\) とすると
並列接続の合成抵抗の公式から
\(\cfrac{1}{R_0}=\cfrac{1}{R}+\cfrac{1}{R}=\cfrac{2}{R}\)
式を変形すると
\(R_0=\cfrac{R}{2}\)
１つの抵抗値の \(\cfrac{1}{2}\) になります。
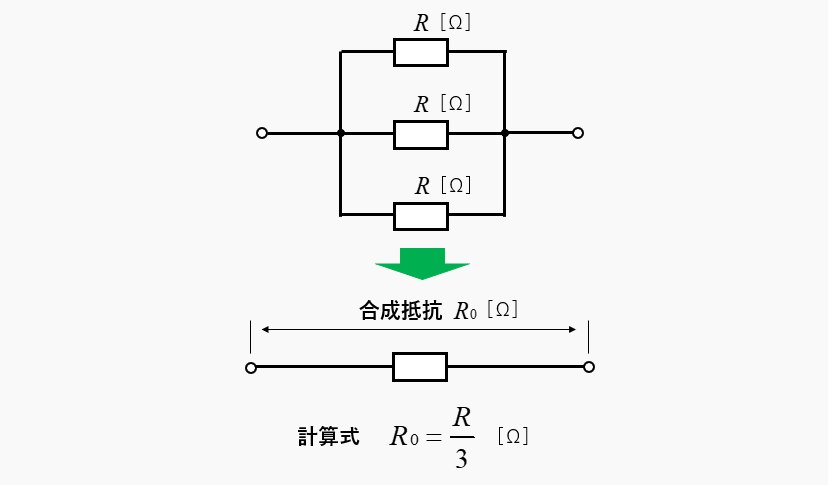
並列接続された3つの抵抗値が同じ場合の合成抵抗は1/3になる
3つの並列接続の 抵抗値が同じ 場合の合成抵抗の求め方。
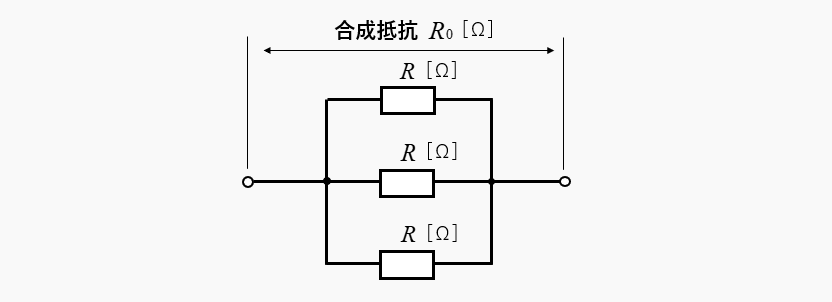
- 3つの抵抗値が同じ場合
-
合成抵抗 \(R_0=\cfrac{R}{3}\) [Ω]
１つの抵抗値の \(\cfrac{1}{3}\) になります。
1/3になることを並列接続の合成抵抗の公式から求める
１つの抵抗値の \(\cfrac{1}{3}\) になる理由を、並列接続の合成抵抗の公式から求める。
並列接続の合成抵抗の公式
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}\)
3つの抵抗値が同じ場合は
\(R_1、R_2、R_3=R\) とすると
並列接続の合成抵抗の公式から
\(\cfrac{1}{R_0}=\cfrac{1}{R}+\cfrac{1}{R}+\cfrac{1}{R}=\cfrac{3}{R}\)
式を変形すると
\(R_0=\cfrac{R}{3}\)
１つの抵抗値の \(\cfrac{1}{3}\) になります。
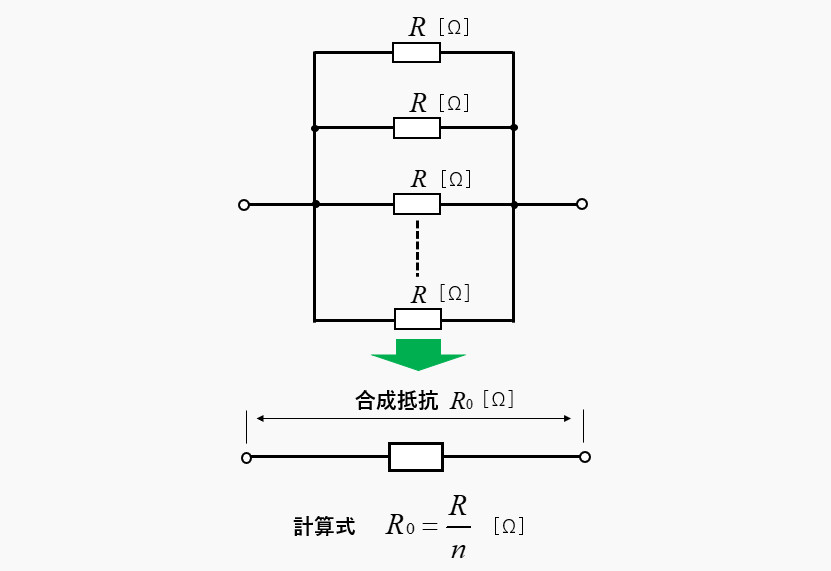
\(n\) 個の抵抗の値が同じ場合の合成抵抗は1/ｎになる
\(n\) 個の並列接続の公式は、次のようになります。
- \(n\) 個の抵抗値が同じ場合
-
合成抵抗 \(R_0=\cfrac{R}{n}\) [Ω]
１つの抵抗値の \(\cfrac{1}{n}\) になります。
1/ｎになることを並列接続の合成抵抗の公式から求める
並列接続の合成抵抗の公式
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}+\cdots+\cfrac{1}{R_n}\)
\(n\) 個の抵抗値が同じ場合は
\(R_1、R_2、R_3 \cdots R_n=R\) とすると
並列接続の合成抵抗の公式から
\(\cfrac{1}{R_0}=\cfrac{1}{R}+\cfrac{1}{R}+\cfrac{1}{R}+\cdots+\cfrac{1}{R}=\cfrac{n}{R}\)
式を変形すると
\(R_0=\cfrac{R}{n}\)
1つの抵抗値の \(\cfrac{1}{n}\) になります。
以上で「和分の積の使い方と並列接続された抵抗値が同じ場合の求め方」の説明を終わります。