インピーダンスとは何か？インピーダンスの求め方と公式

インピーダンスとは電圧と電流の比

交流の電源にモーターやテレビなどの電気製品をつなぐと、当然ですが回路に電流が流れます。

このときの回路の　電圧と電流の比　を　インピーダンス　といいます。

インピーダンスは交流回路において　電流の流れを妨げる働きするもの　といえます。

つまり　電流の流れにくさ　を表しています。

インピーダンスを構成するもの

インピーダンスは　抵抗とリアクタンス　で構成されます。

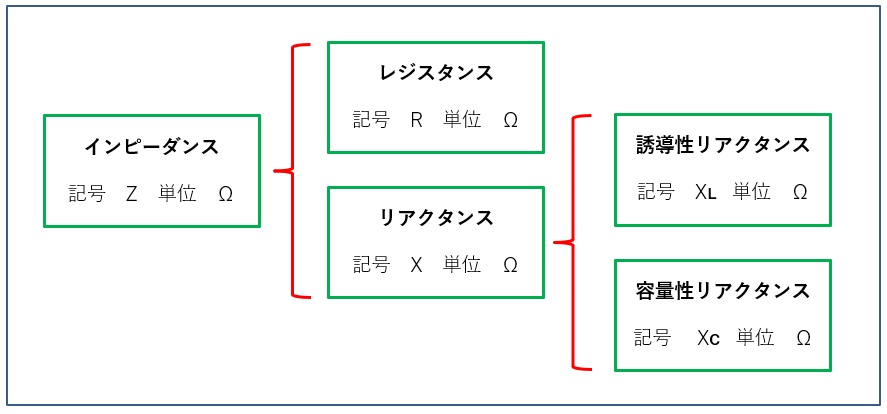
インピーダンスの記号と単位

インピーダンスの記号は　\(\dot{Z}\)　を使います。

インピーダンスの単位は「抵抗」と同じく　[Ω]（オーム）を使います。

一般的に交流回路の負荷は　\(\dot{Z}\)　を使って負荷インピーダンスを表します。

\(\dot Z\)

また、ベクトルを　\(Z\)　で表し、大きさを　\(|Z|\)　絶対値で表す場合もあります。

インピーダンスの　記号には　\(Z\)　を使い、単位には抵抗と同じようにオーム　[Ω]　を使います。

インピーダンスの記号法表示

インピーダンスを記号法で表示すると

実数部と虚数部がある。

\(Z=R+jX\)　[Ω]　

インピーダンスの実数部

実数部は抵抗の部分でレジスタンス　\(R\)　になる。

記号は　\(R\)　で単位は　[Ω]　を使う。

インピーダンスの虚数部

虚数部はリアクタンスの　\(jX\)　になる。

記号は　\(X\)　で単位は　[Ω]　を使う。

誘導性リアクタンス

誘導性リアクタンスは　\(X_L\)　になる。

記号は　\(X_L\)　で単位は　[Ω]　を使う。

容量性リアクタンス

容量性リアクタンスは　\(X_C\)　になる。

記号は　\(X_C\)　で単位は　[Ω]　を使う。

コイルとコンデンサの位相の覚え方

交流回路に　コイルやコンデンサ　を接続すると　電圧と電流の　位相　に　進みや遅れ　が生じます。

交流回路においても、オームの法則が成立します

★　オームの法則は交流回路でも使うことができます。

\(R=\cfrac{V}{I}\)　[Ω]

次の式を見れば分かる通り　抵抗　\(R\)　の部分が　インピーダンス　\(Z\)　に変わっただけです。

\(\dot{Z}=\cfrac{\dot{V}}{\dot{I}}\)　[Ω]　\(\cdots\)インピーダンス

\(\dot{V}=\dot{Z}\dot{I}\)　[V]　\(\cdots\)　電圧

\(\dot{I}=\cfrac{\dot{V}}{\dot{Z}}\)　[A]　\(\cdots\)　電流

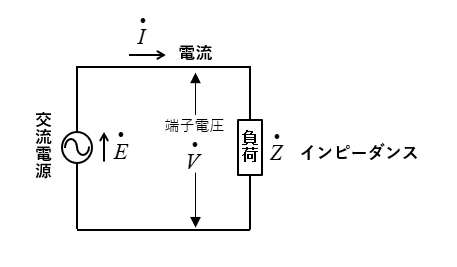
図のように　抵抗、コイル、コンデンサ　が直列の

負荷　\(\dot{Z}\)　を交流電源　\(\dot{E}\)　に接続した回路の

端子電圧を　\(\dot{V}\)　電流を　\(\dot{I}\)　とします。

このときの、電圧　\(\dot{V}\)　と電流　\(\dot{I}\)　の比が　インピーダンス　です。

リアクタンスの大小で誘導性・容量性に変化する

インピーダンスは　抵抗　と　リアクタンス　で構成されています。

リアクタンスの大小

• \(X_L>X_C\)　のときは　誘導性リアクタンス
• \(X_L < X_C\)　のときは　容量性リアクタンス

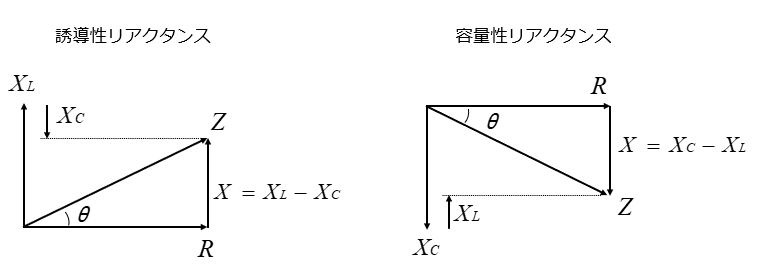
誘導性リアクタンス

誘導性リアクタンスの　インピーダンス　を図にすると、次のようになります。

誘導性リアクタンス

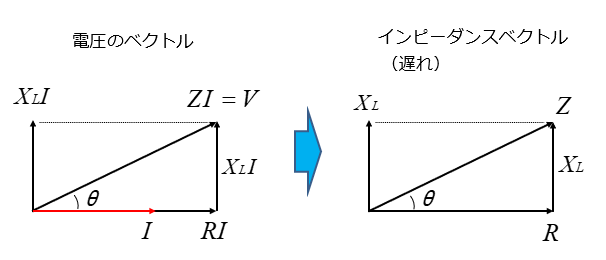
電圧のベクトルから電流を取り除くと　インピーダンスベクトル　になります。

この回路においては、誘導性リアクタンス 　が大きいので力率は　遅れ力率　　になります。

一般的に　力率の遅れや進み　は　電圧を基準　にして考えます。

遅れ力率　を改善するためのものとして、進相コンデンサ　を使用することがあります。

抵抗とコイルを直列に接続した回路は　RL直列回路　といいます。

容量性リアクタンス

容量性リアクタンスの　インピーダンス　を図にすると、次のようになります。

容量性リアクタンス

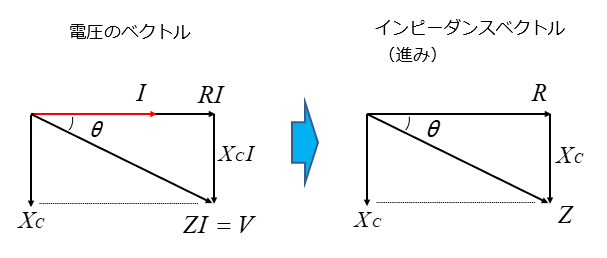
電圧のベクトルから電流を取り除くとインピーダンスベクトルになります。

この回路においては、容量性リアクタンス　が大きいので力率は　進み力率　になります。

一般的に　力率の遅れや進み　は　電圧を基準　にして考えます。

進み力率を改善するためのものとして、分路リアクトル　を使用することがあります。

抵抗とコンデンサを直列に接続した回路は　RC直列回路　といいます。

直列回路のインピーダンスの求め方

直列回路では電流を基準に考える

直列回路では回路を流れる電流　\(I\)　が共通になるので　電流を基準にベクトルを描きます。

★　図のように、抵抗、コイル、コンデンサが　直列　に接続されている回路があります。

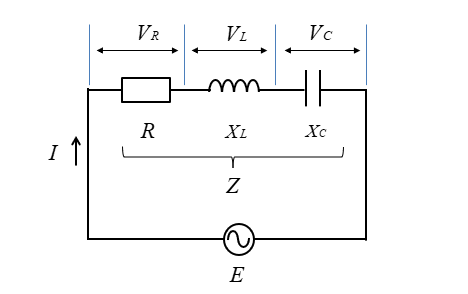
この回路のインピーダンスベクトルは、次のようになります。

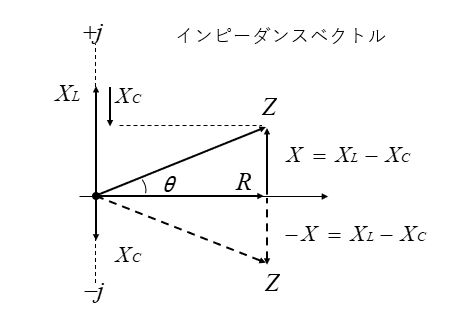
インピーダンスを記号法で表示する

★　インピーダンス　\(Z\)　を記号法で表すと、次のようになります。

\(Z=R+j(X_L-X_C)\quad\rm[Ω]\)　になります。

\(X=X_L-X_C\)　の値が　プラスなら　誘導性リアクタンス　になり

\(X=X_L-X_C\)　の値が　マイナスなら　容量性リアクタンス　になります。

インピーダンスベクトル図からわかるように、合成インピーダンスは三平方の定理で求められます。

\(Z=\sqrt{R^2+X^2}\)\(=\sqrt{R^2+(X_L-X_C)^2}\)　[Ω]

カッコ内の　\((X_L-X_C)\)　は、\(X_C\)　が大きいと値がマイナスになリますが、２乗をするとプラスになるので気にする必要はありません。

回路の電流は

\(I=\cfrac{E}{Z}\)　[A]

各素子の端子電圧は、次のようになります。

\(V_R=RI\)　[V]

\(V_L=X_LI\)　[V]

\(V_C=X_CI\)　[V]

例　題

図のような交流回路があります。

電源電圧の実効値　\(100\)　[V]

抵抗　\(40\)　[Ω]

コイルのリアクタンス　\(80\)　[Ω]

コンデンサのリアクタンス　\(50\)　[Ω]

のとき全体のインピーダンス　\(Z\)　[Ω]　と　回路に流れる電流　\(I\)　[A]　を求めよ。

＜解答例＞

抵抗の値、コイルとコンデンサのリアクタンスが

わかっているので、インピーダンスは次の式で求められます。

\(Z=\sqrt{R^2+(X_L-X_C)^2}\)\(Z=\sqrt{40^2+(80-50)^2}=50\)　[Ω]

電流はオームの法則から

\(I=\cfrac{100}{50}=2\)　[A]　になります。

並列回路のインピーダンスの求め方

並列回路では電圧を基準に考える

並列回路では回路に掛かる電圧　\(E\)　が共通になるので　電圧を基準にベクトルを描きます。

★　図のように、抵抗、コイル、コンデンサが　並列　に接続されている回路があります。

この回路のインピーダンスを　逆数　で表すと、次のようになります。

\(\cfrac{1}{Z}=\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}\)　[Ω]

回路に流れる電流　\(I\)　は

\(I=\cfrac{E}{Z}\)\(=E\left(\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}\right)\)　[A]　\(\cdots(1)\)

★　各素子に流れる電流は、次のようになります。

\(I_R=\cfrac{E}{R}\)　[A]

\(I_L=\cfrac{E}{jX_L}\)\(=-j\cfrac{E}{X_L}\)　[A]

\(I_C=\cfrac{E}{-jX_C}\)\(=j\cfrac{E}{X_C}\)　[A]

各電流をベクトル図にすると、次のようになります。

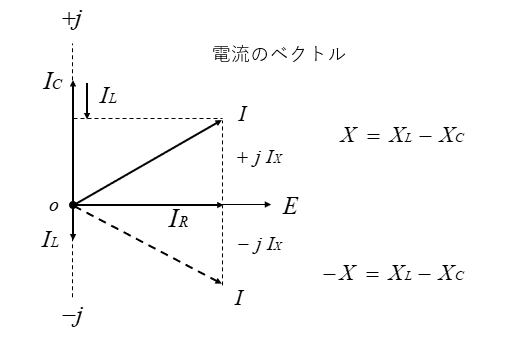
電流のベクトル図からわかるように、回路に流れる電流　\(I\)　は三平方の定理で

\(I=\sqrt{{I_R}^2+{I_X}^2}\)\(=\sqrt{{I_R}^2+(I_L-I_C)^2}\)\(\cdots(2)\)　で求められます。

カッコ内の　\((I_L-I_C)\)　は、\(I_C\)　が大きいと値がマイナスになリますが、２乗をするとプラスになるので気にする必要はありません。

式（2）を変形すると

\(I=\sqrt{{I_R}^2+(I_L-I_C)^2}\)\(=\sqrt{\left({\cfrac{E}{R}}\right)^2+\left(\cfrac{E}{ωL}-ωCE\right)^2}\)

\(I=E\sqrt{\left({\cfrac{1}{R}}\right)^2+\left(\cfrac{1}{ωL}-ωC\right)^2}\cdots(3)\)

式（3）の両辺を　\(E\)　で割ります。

\(\cfrac{I}{E}=\cfrac{1}{Z}=\cfrac{E}{E}\sqrt{\left({\cfrac{1}{R}}\right)^2+\left(\cfrac{1}{ωL}-ωC\right)^2}\)

★　インピーダンス　\(Z\)　は

\(Z=\cfrac{1}{\sqrt{\left({\cfrac{1}{R}}\right)^2+\left(\cfrac{1}{ωL}-ωC\right)^2}}\)　で求められます。

並列回路のインピーダンスの求め方

RLC並列回路でインピーダンスを求める場合は

RLC並列回路に流れる電流を求めて

\(Z=\cfrac{E}{I}\)　

から求めるほうが簡単な場合が多いです。

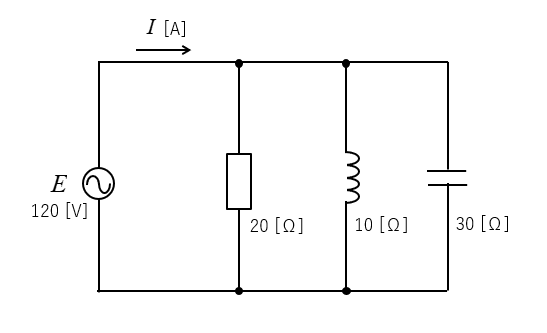
例　題

図のようなRLC並列回路があります。

電流　\(I\)　と　全体のインピーダンス　\(Z\)　を求めよ。

＜解答例＞

抵抗を流れる電流を　\(I_R\)　

コイルを流れる電流を　\(I_L\)　

コンデンサを流れる電流を　\(I_C\)　とします。

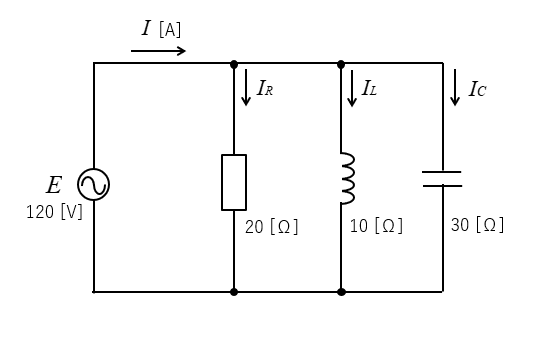
\(I_R=\cfrac{E}{R}\)\(=\cfrac{120}{20}=6\)　[A]

\(I_L=\cfrac{E}{X_L}\)\(=\cfrac{120}{10}=12\)　[A]

\(I_C=\cfrac{E}{X_C}\)\(=\cfrac{120}{30}=4\)　[A]

回路の電流　\(I\)　は

\(I=\sqrt{6^2+(12-4)^2}=10\)　[A]　

回路のインピーダンスは

\(Z=\cfrac{E}{I}=\cfrac{120}{10}=12\)　[Ω]　になります。

ややこしい虚数単位　j　の付け方

交流回路のインピーダンスを複素数で表示するとき、虚数単位の　\(j\)　がでてきます。

この　\(j\)　の付け方について　簡単な方法があります。

虚数単位の　\(j\)　は、2乗すると　-1　になります。

虚数単位　\(j\)　を付ける場所

• 虚数単位がややこしくなるのは、どこに付けたらいいかわからない。
• \(+j、-j\)　どっちになるかわからない。ということではないでしょうか

虚数単位　\(j\)　は、\(ω\)（オメガ）の前に　\(+j\)　を付けると覚えましょう。

これだけを覚えておけば、かなりの部分が解決すると思います。

虚数単位の意味

虚数単位にはどんな意味があるかというと

次のような意味があります。

リアクタンスの表示方法

★　\(j\)　を　\(ω\)　の前に付けると覚えておけば、あとは式を変形するだけで符号の変化もわかります。

リアクタンス	数式
誘導性リアクタンス	\(X_L=ωL\)	\(X_L=jωL\)	\(jX_L=jωL\)
容量性リアクタンス	\(X_C=\cfrac{1}{ωC}\)	\(X_C=\cfrac{1}{jωC}\)	\(-jX_C=-j\cfrac{1}{ωC}\)

誘導性リアクタンスの表示方法

誘導性リアクタンスは、\(ωL、X_L\)　と表します。

虚数単位を　\(ω\)　の前につけると、\(jωL\)　となります。

\(X_L=ωL\)

\(X_L=jωL\)

\(jX_L=jωL\)

容量性リアクタンスの表示方法

容量性リアクタンスは、\(\cfrac{1}{ωC}、X_C\)　と表します。

虚数単位を　\(「ω」\)　の前につけると、\(\cfrac{1}{jωC}\)　となります。

\(X_C=\cfrac{1}{ωC}\)

\(X_C=\cfrac{1}{jωC}\)

\(-jX_C=\cfrac{1}{jωC}\)

容量性リアクタンスは、分数になるので　\(j\)　があるとややこしくなります。

しかし、前述のように　\(「ω」\)　の前につけるとすれば

\(\cfrac{1}{jωC}\)

の分子と分母に　\(j\)　を掛けると、次のように表すことができます。

\(\cfrac{1}{jωC}\)\(=\cfrac{j}{j}×\cfrac{1}{jωC}\)\(=\cfrac{j×1}{j^2ωC}=\cfrac{j}{-ωC}\)\(=-j\cfrac{1}{ωC}=-jX_C\)

インピーダンス回路のまとめ

RLC直列回路のまとめ

RLC直列回路
インピーダンス	記号法	\(Z=R+j(X_L-X_C\) [Ω]
	大きさ	\(Z=\sqrt{R^2+X^2}\) [Ω]
		\(Z=\sqrt{R^2+(X_L-X_C)^2}\) [Ω]
電流	大きさ	\(I=\cfrac{E}{Z}\) [A]
		\(I=\cfrac{E}{\sqrt{R^2+(ωL-\cfrac{1}{ωC})^2}}\) [A]
		\(I=\sqrt{{I_R}^2+{I_X}^2}\) [A]
		\(I=\sqrt{{I_R}^2+(I_L-I_C)^2}\) [A]
端子電圧	大きさ	\(V_R=RI\) [V]
		\(V_L=X_LI\) [V]
		\(V_C=X_CI\) [V]

RLC並列回路のまとめ

RLC直列回路
インピーダンス	記号法	\(\cfrac{1}{Z}=\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}\) [Ω]
電流	記号法	\(I=E\left(\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}\right)\) [A]
	大きさ	\(I=\sqrt{{I_R}^2+(I_L-I_C)^2}\) [A]
各素子の電流	記号法	\(I_R=\cfrac{E}{R}\) [A]
		\(I_L=\cfrac{E}{jX_L}\) [A]
		\(I_C=\cfrac{E}{-jX_C}\) [A]
	大きさ	\(I_L=\cfrac{E}{X_L}\) [A]
		\(I_C=\cfrac{E}{X_C}\) [A]

練習問題

問題1

図のように　RLC直列回路があるとき

回路に流れる電流　\(I\)　[A]　を求めよ。

＜解答例＞

合成インピーダンスの式から

\(Z=\sqrt{R^2+(X_L-X_C)^2}\)

\(Z=\sqrt{16^2+(20-8)^2}\)\(=\sqrt{400}=20\)　[Ω]

電流　\(I\)　は

\(I=\cfrac{E}{Z}=\cfrac{100}{20}=5\)　[A]　になります。

問題2

図の回路に流れる電流　\(\dot{I}\)　[A]　と大きさ　\(I\)　[A]　を求めよ。

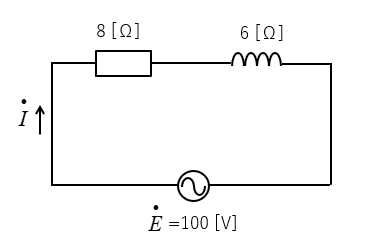
＜解答例＞

合成インピーダンス　\(\dot Z\)　は

\(\dot Z=R+jX=8+j6\)　[Ω]

電流　\(\dot{I}\)　[A]　は

\(\dot I=\cfrac{\dot E}{\dot Z}\)

\(\dot I=\cfrac{100}{8+j6}\)\(=\cfrac{100(8-j6)}{(8+j6)(8-j6)}\)

\(\dot I=8-j6\)

電流の大きさ　\(I\)　は

\(I=\sqrt{{I_R}^2+{I_X}^2}\)\(=\sqrt{8^2+6^2}=10\)　[A]

問題3

抵抗　\(30\)　[Ω]　自己インダクタンス　\(0.1273\)　[H]　

の直列回路に交流電圧　\(100\)　[V]　を加えたところ

回路に　\(2\)　[A]　の電流が流れた。

この回路のインピーダンス、誘導リアクタンス、及び周波数を求めよ。

＜解答例＞

問題を回路図にすると、次のようになります。

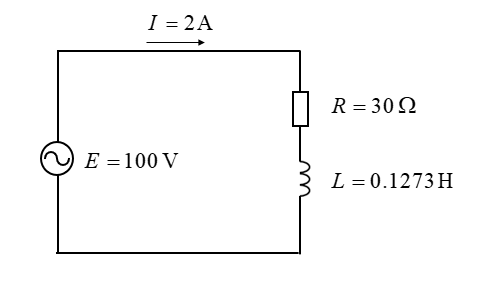
回路のインピーダンス \(Z\) は

\(Z=\cfrac{E}{I}=\cfrac{100}{2}=50\)　[Ω]

誘導リアクタンス \(X_L\) は

\(X_L=\sqrt{Z^2-R^2}=\sqrt{50^2-30^2}=40\)　[Ω]

周波数　\(f\)　は

\(X_L=2πfL=40\)　[Ω]

\(f=\cfrac{40}{2πL}=\cfrac{40}{2π×0.1273}\fallingdotseq 50\)　[Hz]　になります。

以上で「インピーダンスとは何か？インピーダンスの求め方と公式」の説明を終わります。