交流回路の電圧や電流は時間と共に、波形の位置が違ってきます。電圧や電流の波形の位置のことを「位相」といいます。
交流回路の「位相と位相差」、「位相の進みや遅れ」について説明します。
位相とは

円運動をしている時の波形は、図のように正弦波で表すことができます。位相とは、電圧や電流などの波形の位置を示す用語です。
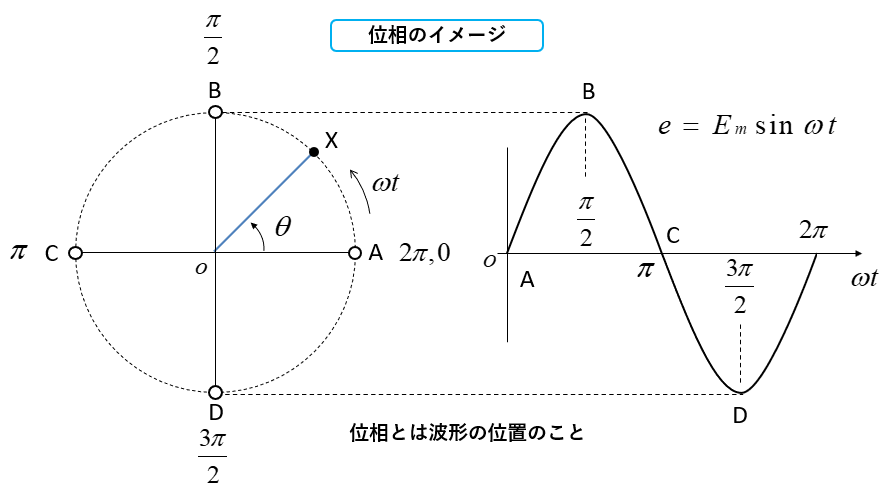
Aの位相:\(0\)(ゼロ)、Bの位相:\(\cfrac{π}{2}\) 、Cの位相:\(π\) 、Dの位相:\(\cfrac{3π}{2}\) 、Aの位相:\(π\) 又は \(0\) を繰り返します。
電圧を \(e=E_m\sinωt\) とすれば、次のようになります。
Aの位相:\(e=E_m\sinωt\)
Bの位相:\(e=E_m\sin(ωt+\cfrac{π}{2})\)
Cの位相:\(e=E_m\sin(ωt+π)\)
Dの位相:\(e=E_m\sin(ωt+\cfrac{3π}{2})\)
このように、位相とは周期的な波形をするものが、その周期中のどの位置にいるかを示すことをいいます。
位相と位相角
\(e=E_m\sinωt\) や \(e=E_m\sin(ωt+θ)\) の式において
\(ωt\) や \((ωt+θ)\) を 位相 または 位相角 といいます。
初期位相と初期位相角
\(e=E_m\sinωt\) や \(e=E_m\sin(ωt+θ)\) の式において
\(t=0\) のときの位相 を 初期位相 または 初期位相角 といいます。
位相差とは
位相差とは、同一周波数の2つの波形の「位相の差」をいいます。この場合、振幅の大きさは関係ありません。
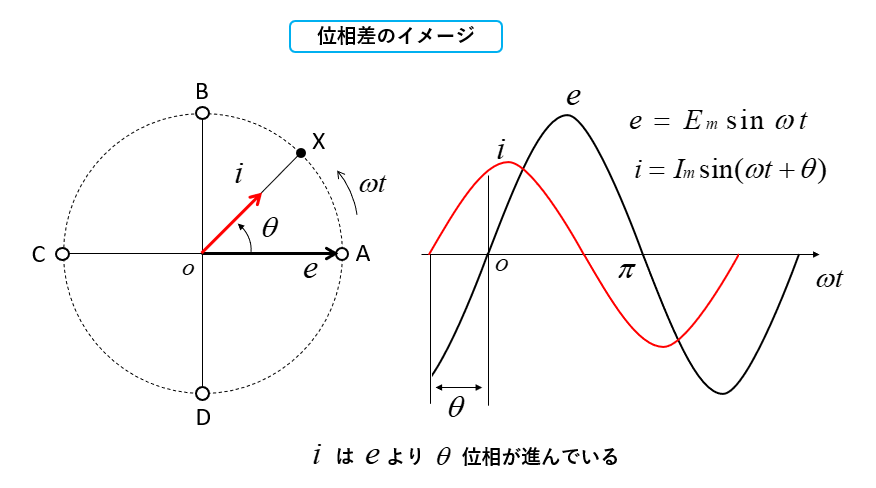
電気回路の電圧 \(e\) と電流 \(i\) の位相が \(θ\) ずれています。この電圧と電流のように、同じ周期だが位相にずれがある時、この「位相のずれ」を位相差といいます。
位相差の求め方
位相差を求めるには、周期が同じ位相であることが前提になります。
位相差を求める式は、位相差=比較したい位相-基準の位相 となります。
比較したい位相=\(\sin(ωt+θ)\)
基準の位相=\(\sinωt\)
位相差=\((ωt+θ)-ωt=θ\) [rad]
振幅の大きさは位相差には関係しない
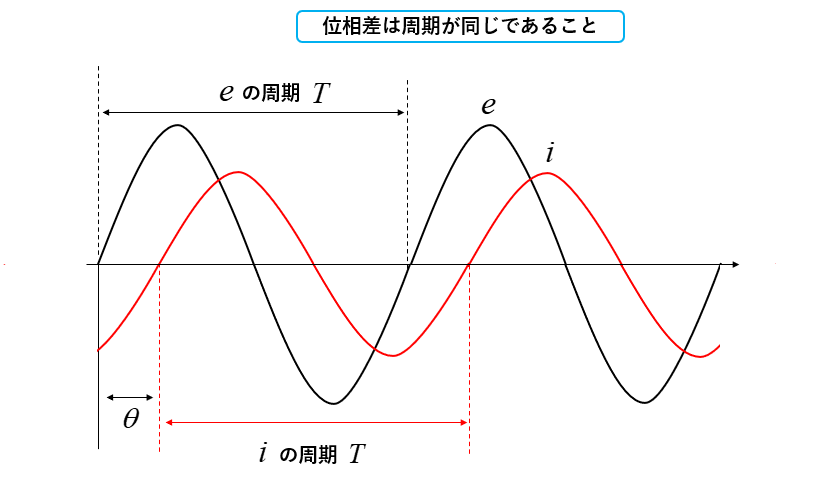
位相差は周期(周波数)が同じであれば、振幅の大きさは関係ありません。
\(e\) の周期と \(i\) の周期が等しい。
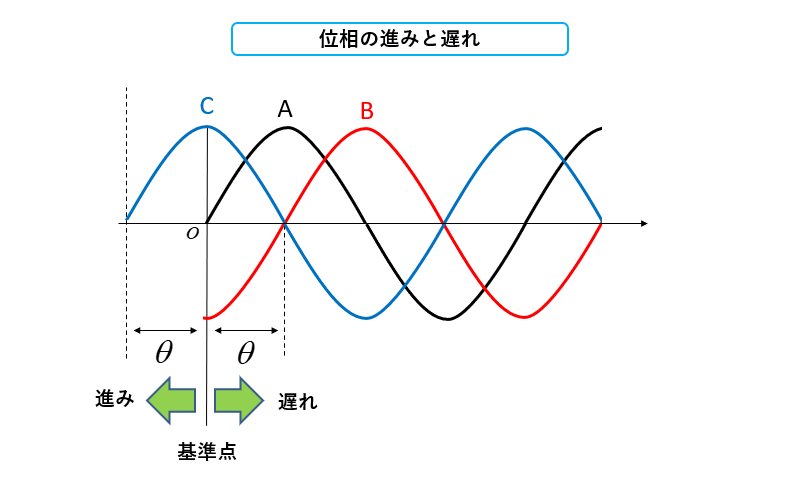
位相の進みと遅れ
位相の進みと遅れは、基準点から見てある時点の位相を比較すれば分かります。
位相Aのゼロを基準点として、位相Bがゼロになるのは \(θ\) 後ですから「遅れ」と言えます。同じように考えて、位相Aがゼロの時、位相Cは \(θ\) 前にゼロになっていますので「進み」と言えます。
まとめ
交流回路の電圧や電流の、波形の位置のことを位相といいます。
周期が同じ2つの波形の位相のずれのことを、位相差といいます。
位相の進みと遅れは、基準点から見た時の位相の位置のことです。基準点の右側に位相差がある時は遅れで、左側に位相差がある時は進みです。
以上で「位相と位相差とは」の説明を終わります。