交流の特徴は直流と違って、大きさと向きが時間の経過とともに変化していることです。
交流の表し方、交流が正弦波交流になること、交流回路の約束事などについて説明します。
交流の表し方
交流回路では、図のように時間の経過にと共に、交流電圧の大きさと向きが周期的に変化しています。
当然ですが、回路に流れる電流も大きさと向きが周期的に変化しています。
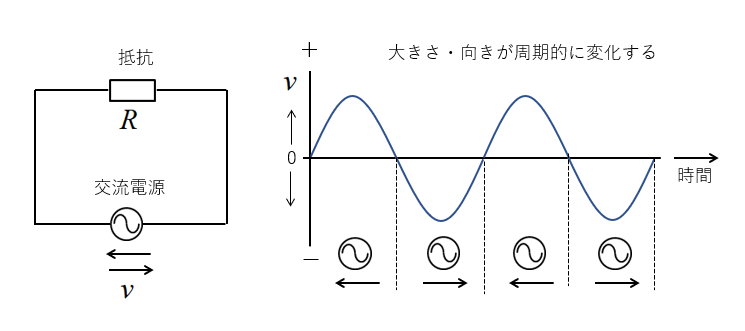
■ 交流の瞬時値と最大値
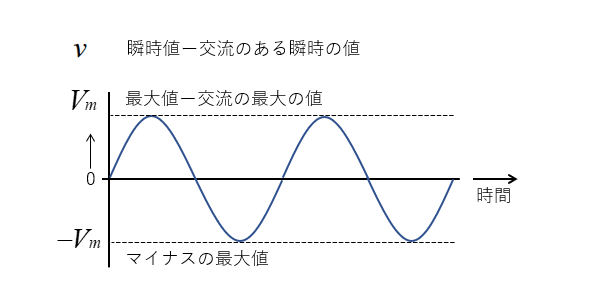
交流の瞬時値と最大値 には次のような意味があります。
- \(V\cdots\)瞬時値 その交流の「ときどきの値」を表します。
- \(V_m\cdots\)最大値 その交流の最大値を表します。
- \(-V_m\cdots\)最大値 その交流のマイナスの最大値を表します。
- \(E、V\cdots\)実効値 直流電力と同じ仕事をするときの、交流の値を表します。
交流の周期と周波数
同じ波形の一区切りを「周期」と呼び、記号を \(T\)、 単位を [s] で表します。
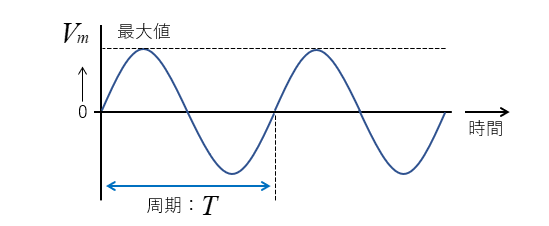
周期は(0から0)と限らず、どこの波形をとってもかまいません。
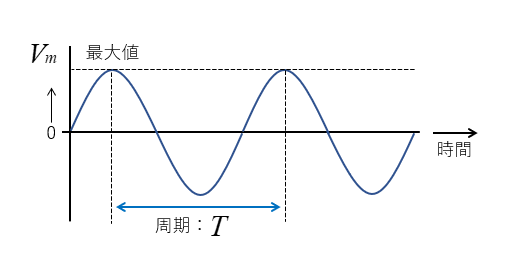
1秒間に繰り返す周期の数を周波数と呼び、記号を \(f\)、 単位を [Hz] で表します。
もし \(f=50\) [Hz] のときは
\(T=\cfrac{1}{50}\) [s] になります。
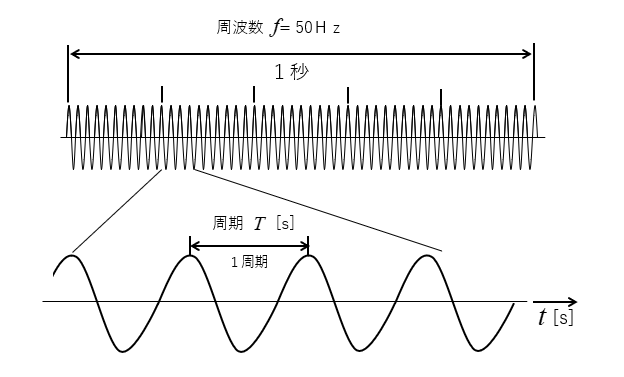
■ 周期と周波数の関係
周期と周波数の間には、次の関係があります。
\(T=\cfrac{1}{f}\) [s]
\(f=\cfrac{1}{T}\) [Hz]
交流を数式で表す
瞬時値 \(v\) を数式で表すと次のようになります。
\(v=V_m\sinωt\cdots(1)\)
\(ω\)(オメガ)は角速度のことで、1秒間に進む角度を表します。
単位は [rad/s] を使います。
\(ω=2πf\) [rad/s]
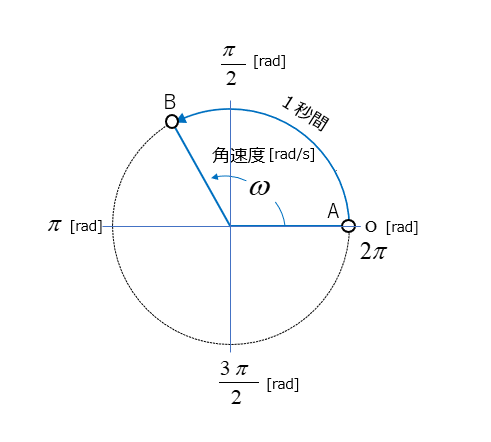
式(1)に \(ω=2πf\) を代入すると
\(v=V_m\sin2πft\) になります。
■ 横軸を時間で表示する
周波数を 60 [Hz] とすると
\(v=V_m\sin120πt\) になります。
次の図は、瞬時値を時間で表したものです。
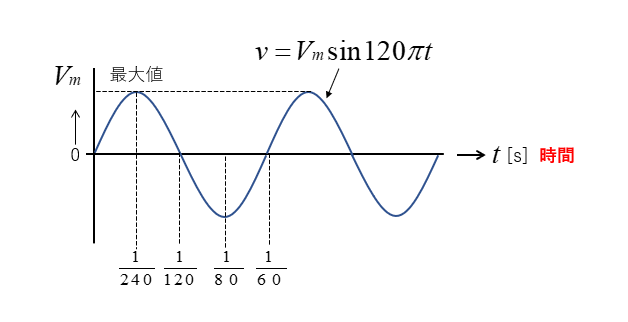
\(t=\cfrac{1}{240}\) [s] を代入すると
\(v=V_m\sin\cfrac{π}{2}\)
\(\sin\cfrac{π}{2}=1\) なので
\(v=V_m\) になります。
\(t=\cfrac{1}{120}\) [s] を代入すると
\(v=V_m\sinπ\)
\(\sinπ=0\) なので
\(v=0\) になります。
\(t=\cfrac{1}{80}\) [s] を代入すると
\(v=V_m\sin\cfrac{3π}{2}\)
\(\sin\cfrac{3π}{2}=-1\) なので
\(v=-V_m\) になります。
\(t=\cfrac{1}{60}\) [s] を代入すると
\(v=V_m\sin2π\)
\(\sin2π=0\) なので
\(v=0\) になります。
■ 横軸を角度で表示する
交流回路では横軸を時間ではなく、角度で表現します。
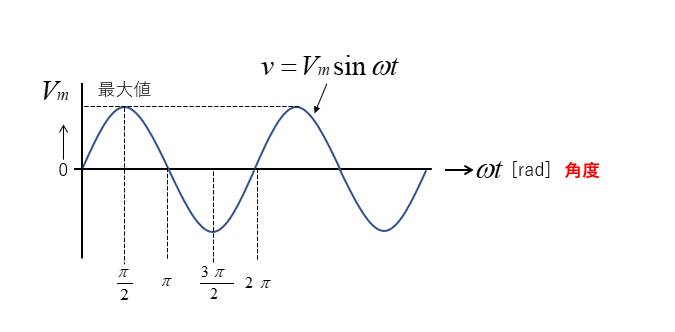
■ 1周期は\(2π\) [rad]
角速度を使うことで、周波数に関係なく交流を表現することができます。
位相と位相差
位相と位相差 について
■ 位相の遅れ
次の図において、\(v_2\) の位相の考え方について説明します。
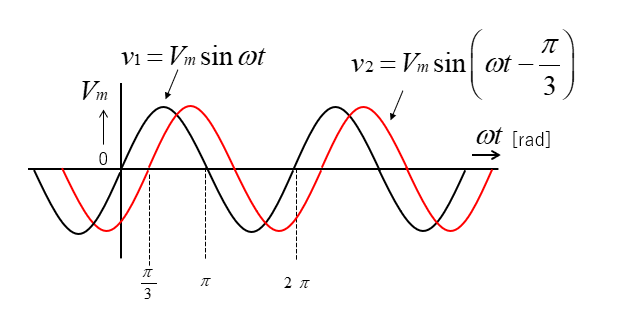
\(v_2=V_m\sin(ωt-\cfrac{π}{3})\) となりますが
どのようにして \(-\cfrac{π}{3}\) を求めたら良いのでしょうか。
★ 考え方
\(v_2\) は \(\sinωt=\sin(\cfrac{π}{3}+x)=0\) になれば良いので
\(x=-\cfrac{π}{3}\) となります。
\(v_2=V_m\sin(\cfrac{π}{3}-\cfrac{π}{3})\)\(=V_m\sin0=0\)
位相差は、\(v_1\) に対して \(v_2\) は \(\cfrac{π}{3}\) 遅れていることになります。
値(あたい)がゼロになるところを比較すればわかります。
■ 位相の進み
次の図において、\(v_3\) の位相の考え方について説明します。
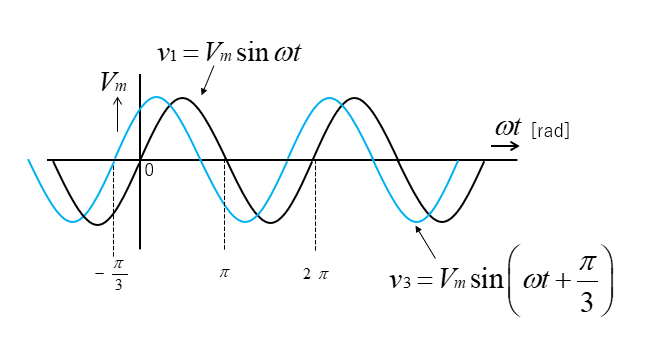
\(v_3=V_m\sin(ωt+\cfrac{π}{3})\) となります。
★ 考え方
\(v_3\) は \(\sinωt=\sin(-\cfrac{π}{3}+x)=0\) になれば良いので
\(x=+\cfrac{π}{3}\) となります。
\(v_3=V_m\sin(-\cfrac{π}{3}+\cfrac{π}{3})\)\(=V_m\sin0=0\)
位相差は、\(v_1\) に対して \(v_3\) は \(\cfrac{π}{3}\) 進んでいることになります。
値がゼロになるところを比較すればわかります。
コイルが起電力を発生する時に正弦波になる理由
交流が正弦波になるのは、当たり前と思って疑問を待たなかったのですが、どうしてかと疑問になります。
別に、どうでも良いことかもしれませんが、自分なりに考えてみました。
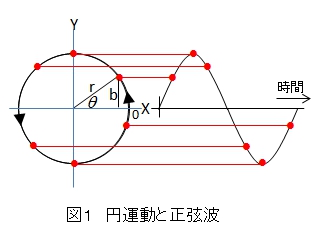
図1を見ると分かるように、円運動をする時のY軸のX軸からの位置をbとして、グラフ化すると正弦波になることが分かります。
コイルが磁界を切る時の方向
コイルの位置が水平の時は、磁界を垂直に切る部分がありません。
コイルに起電力が発生するためには、コイルが磁界を垂直に切らなければなりません。
辺cは円周に対して常に直角に動きます。
\(X-Y\) のコイルが \(X_1-Y_1\) まで角度 \(θ\) 動いた場合、コイルが磁界を垂直に切る部分は辺 b になります。
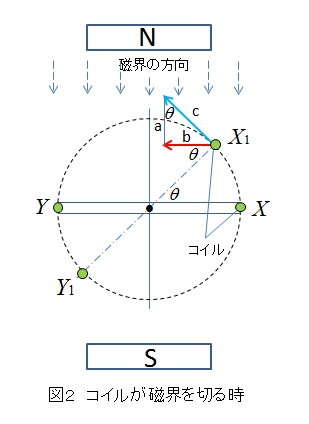
■ 図2でコイルが水平から磁石のN極に近づいて行く時、N極からの磁界が強くなっていきます。
- 発生する起電力はだんだんと強くなります。
- そして、N極まで来た時が最大になります。
- N極から遠ざかる時起電力は弱くなっていき、水平になった時がゼロになります。
- そして、これを繰り返します。
起電力は磁界を垂直に切る時に発生するので、コイルが磁界を垂直に切るのは赤の矢印のbの部分になリます。
■ 磁界を垂直に切る部分
磁界を垂直に切る部分は \(b=c\sinθ\) となります。
コイルが回転する時に、コイルが垂直に磁界を切る時だけ起電力ができます。
これはサインの値に比例しますので、これが交流が正弦波になる理由です。

正弦波交流には、瞬時値と最大値、実効値、平均値 などがあります。
単相交流とは
単相交流とは、図のように1つの交流電気が流れているものをいいます。
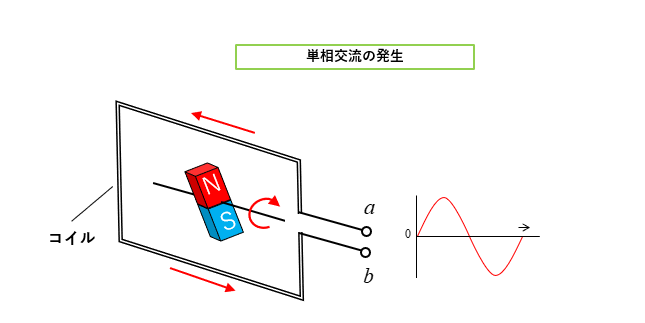
単相交流はコイルの中に磁石を配置して、磁石を回転させることで 電磁誘導 により、端子ab間に交流起電力を発生することができます。
単相交流は正弦波交流になり、瞬時値を \(e\) 最大値を \(E_m\) 実効値を \(E\) とすると次のように表されます。
\(e=E_m\sinωt\) [V]
\(e=\sqrt2E\sinωt\) [V]
単相交流は家庭で使われますが、実際の配電方式には 単相3線式 という配電方式が使われます。
単相3線式が用いられるのは、単相100ボルトと単相200ボルトの2つの電圧を使うことができるためです。
交流回路の約束事
交流回路の計算をする時は、いくつかの決まりがあります。
その決まりに従って計算する方が、全体の計算が簡単になる場合があります。
■ 求めるものが電圧の時
\(V=ZI\) なので、合成インピーダンスを求める。
■ 求めるものが電流の時
\(I=YI\) なので、合成アドミタンスを求める。
■ インピーダンスが並列接続になっている時
合成アドミタンスを求めるほうが、計算がやりやすくなる場合が多い。
インピーダンスとアドミタンスの関係
インピーダンス と アドミタンス の関係は、次のようになります。
\(Z=\cfrac{1}{Y}\) [Ω]
\(Y=\cfrac{1}{Z}\) [S]
表のようにインピーダンスとアドミタンスは、逆数の関係にあります。

交流回路の特徴
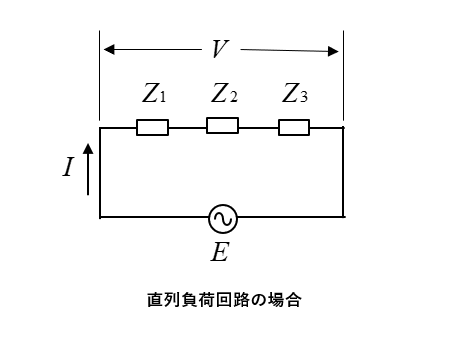
直列負荷回路では、インピーダンスの足し算で計算できるので、合成インピーダンスを求める方がやりやすくなります。
\(V=ZI=(Z_1+Z_2+Z_3)I\) [V] で合成インピーダンスから求める方が簡単になることがあります。
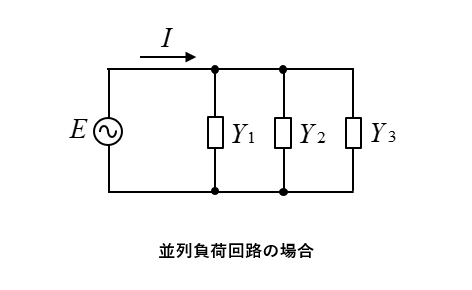
並列負荷回路では、アドミタンスにして計算すると足し算にすることができます。
電流を求める場合は合成アドミタンスで求める方が、計算をやり易くなることがあります。
\(I=YV=(Y_1+Y_2+Y_3)V\) [A]
以上で「交流の表し方と交流が正弦波交流になるわけ」の説明を終わります。