正弦波交流の大きさを表す方法の一つに 平均値 があります。
平均値は、瞬時値の和の平均で表すことができます。
平均値を \(E_{av}\)、最大値を \(E_m\) とすると、平均値は次のように表されます。
\(E_{av}=\cfrac{2}{\pi}E_m\quad\rm[V]\)
交流の波形
正弦波交流の波形は、1周期について平均すると、各半周期の波形の大きさは等しいのでゼロになってしまいます。
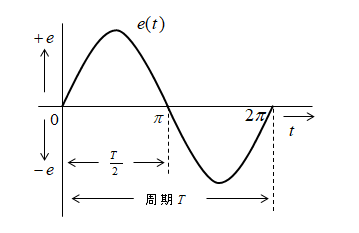
そのため、次のように考えて平均値を求めます。
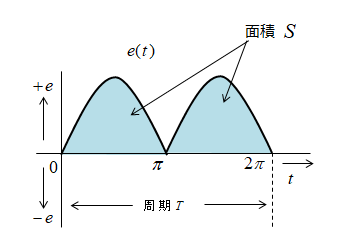
- 絶対値をとる。(正負の面積が同じ場合)
- 波形 1周期分の面積 S を求める。
- 1 周期 \(T\) で割る。
このようにすることで、同じ幅で同じ面積の長方形の高さ(直流振幅)が求められる。
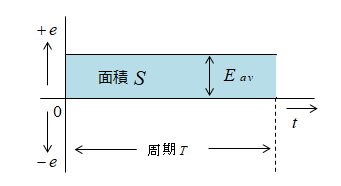
平均値の求め方
図から平均値 \(E_{av}\) を計算してみる。

\(E_{av}=\cfrac{S}{T}=\cfrac{1}{T}\int_0^T|e(t)|dt\)
平均値を求めるのであるから、1つの山について、つまり1/2周期について計算しても同じになります。
\(E_{av}=\cfrac{S}{T}=\cfrac{1}{T}\int_0^T|e(t)|dt\)
\(E_{av}=\cfrac{S/2}{T/2}=\cfrac{1}{T/2}\int_0^{T/2}|e(t)|dt\)
\(E_{av}=\cfrac{2}{T}\int_0^{T/2}|e(t)|dt\)
\(ωt=θ\) とすると
\(E_{av}=\cfrac{2}{T}\int_0^{T/2}E_m\sin θ\rm dθ\)
\(E_m\) は、積分の前に出せますので
\(E_{av}=\cfrac{2E_m}{T}\int_0^{T/2}\sin θ\rm dθ\)
ここで、1周期 \(T=2\pi\) ですから、式に代入すると
\(E_{av}=\cfrac{2E_m}{2\pi}\int_0^{2\pi/2}\sin θ\rm dθ\)
\(E_{av}=\cfrac{E_m}{\pi}\int_0^{\pi}\sin θ\rm dθ\)
この式を展開すると
\(E_{av}=\cfrac{E_m}{\pi}\int_0^{\pi}\sin θ\rm dθ\)
\(E_{av}=\cfrac{E_m}{\pi}\left[-\cos θ\right]_0^{\pi}\)
\(E_{av}=\cfrac{E_m}{\pi}\{-\cos \pi -(-\cos 0)\}\)
三角関数の値から
\(\cos \pi=-1、\cos 0=1\) を上の式に代入する
\(E_{av}=\cfrac{E_m}{\pi}\{-\cos \pi -(-\cos 0)\}\)
\(E_{av}=\cfrac{E_m}{\pi}\{-(-1)-(-1)\}\)
\(E_{av}\)\(=\cfrac{2}{\pi}E_m \fallingdotseq 0.6369E_m\quad\rm[V]\) になります。
■ 積分の式について
\(E_{av}\)\(=\cfrac{E_m}{\pi}\int_0^{\pi}\sin θ \rm dθ\)\(=\cfrac{E_m}{\pi}\left[-\cos θ\right]_0^{\pi}\)
積分の式は次のような意味があると、考えると分かりやすいのではないでしょうか。
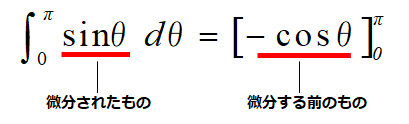
三角関数の知識 を参考にしてください。
\(\cosθ\) の微分は \(-\sinθ\) ですから
微分して \(\sinθ\) になるものは \(-\cosθ\) になります。
したがって、次の式になります。
\(E_{av}\)\(=\cfrac{E_m}{\pi}\int_0^{\pi}\sin θ \rm dθ\)\(=\cfrac{E_m}{\pi}\left[-\cos θ\right]_0^{\pi}\)
以上で「正弦波交流の平均値」の説明を終わります。