三角関数とは 辺と角度の関数 のことで
正弦(サイン・sin)、余弦(コサイン・cos)、正接(タンジェント・tan)などの関数を 三角関数 といいます。
三角関数の値
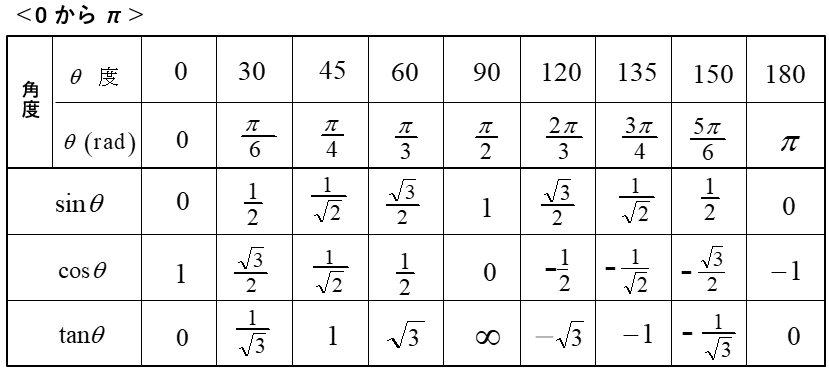
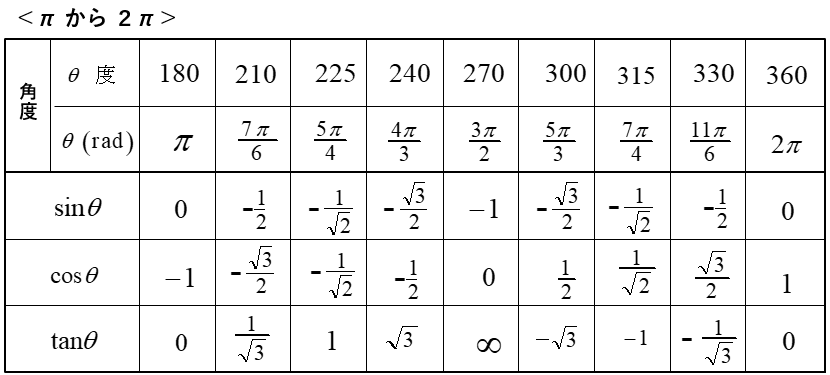
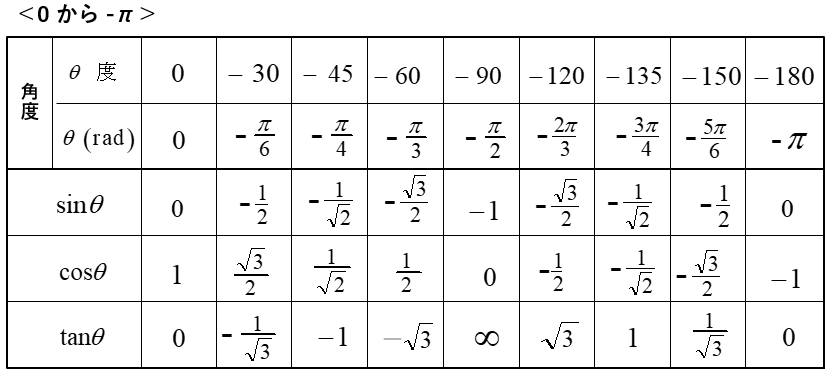
三角関数(\(\sin・\cos・\tan\))は、角度に対してその数値を求める関数です。
例 \(\sin30°=\cfrac{1}{2}\)
逆三角関数の値
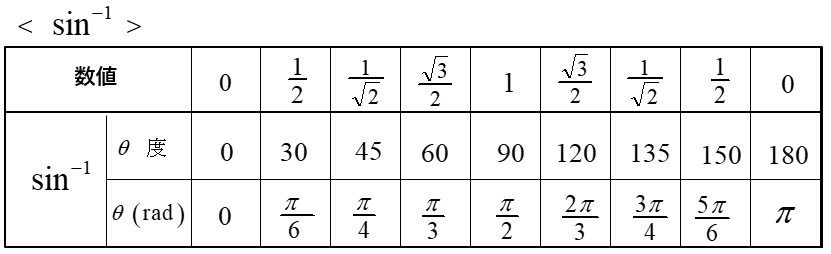
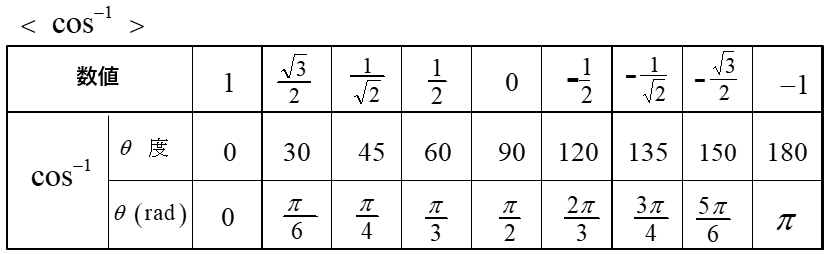
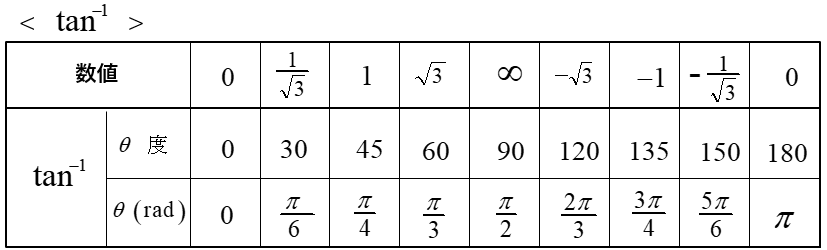
逆三角関数(\(\arcsin・\arccos・\arctan\))は数値に対して角度を求める関数をいいます。
例 \(\arcsin \cfrac{1}{2}=\sin^{-1}\cfrac{1}{2}\)=30°
★ \(\arcsin\)(アークサイン)、\(\arccos\)(アークコサイン)、\(\arctan\)(アークタンジェント)のことを、逆三角関数といいます。
★ \(\sin^{-1}x\) のように表すこともあります。
\(\sin^{-1}x=\arcsin x\)
\(\cos^{-1}x=\arccos x\)
\(\tan^{-1}x=\arctan x\)
三角関数と逆三角関数の関係
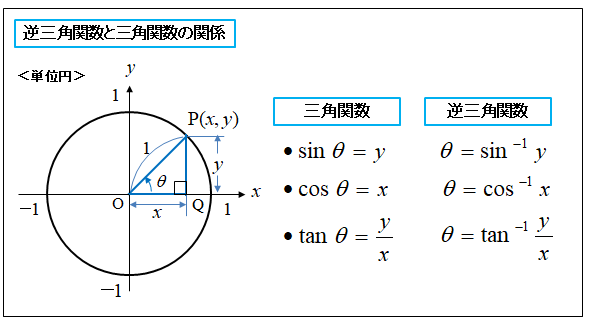
単位円で見ると
\(\sinθ=y\) のとき、\(\arcsin y=\sin^{-1}y=θ\) となります。
\(\cosθ=x\) のとき、\(\arccos x=^cos^{-1}x=θ\) となります。
\(\tanθ=\cfrac{y}{x}\) のとき、\(\arctan \cfrac{y}{x}=\tan^{-1}\cfrac{y}{x}=θ\) となります。
三角関数の公式
\(π\) [rad] の公式

\(\cfrac{π}{2}\) [rad] の公式
■ \(+\cfrac{π}{2}\) [rad] の公式


■ \(-\cfrac{π}{2}\) [rad] の公式

三角関数の合成
\(A\sinθ+B\cosθ=\sqrt{A^2+B^2}\sin(θ+α)\)
三角関数の微分
\((\sin x)’=\cos x\)
\((\cos x)’=-\sin x\)
\(a\) を定数とすると
\((\sin ax)’=a \cos ax\)
\((\cos ax)’=-a \sin ax\)
三角関数の積分
\(∫\sin x dx=-\cos x\)
\(∫\cos x dx=\sin x\)
\(∫\sin ωt dt=-\cfrac{1}{ω}\cos ωt\)
\(∫\cos ωt dt=\cfrac{1}{ω}\sin ωt\)
加法定理

2倍角の公式

三角関数と三角関数の逆数
■ sin(サイン)・cos(コサイン)・tan(タンジェント)の覚え方
図のように、アルファベットの筆記体の書き順で覚えると良いとおもいます。
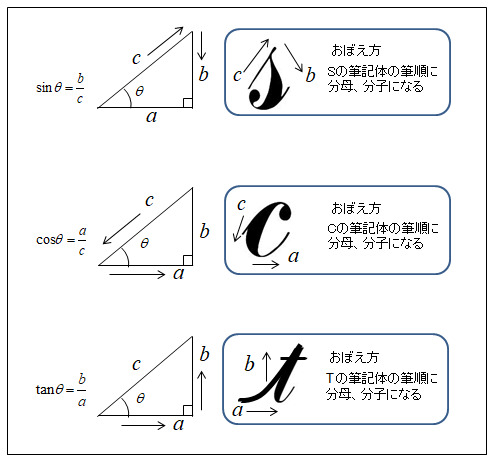
■ 三角関数のsin・cos・tan(正弦・余弦・正接)
三角関数は、直角三角形ABCにおいて、次のように定義されます。
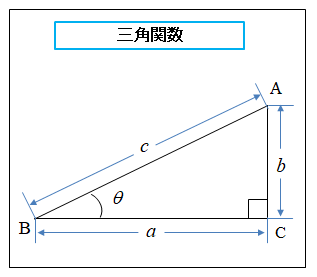
\(\sinθ=\cfrac{b}{c}\)
\(\cosθ=\cfrac{a}{c}\)
\(\tanθ=\cfrac{b}{a}\)
三角関数の逆数
■ 三角関数の逆数は、sec(セカント)、csc(コセカント)、cot(コタンジェント)といいます。
\(\secθ=\cfrac{1}{\cos θ}\)
\(\cscθ=\cfrac{1}{\sin θ}\)
\(\cotθ=\cfrac{1}{\tan θ}\)
■ 三角関数のtanθの定義
tanθは次のように表せます。
\(\tanθ=\cfrac{b}{a}=\frac{\cfrac{b}{c}}{\cfrac{a}{c}}=\cfrac{\sinθ}{\cosθ}\)
また、同様に次のようになります。
\(\sinθ=\tanθ\cosθ\)
\(\cosθ=\cfrac{\sinθ}{\tanθ}\)
単位円の座標と三角関数
三角関数を単位円で見てみましょう。
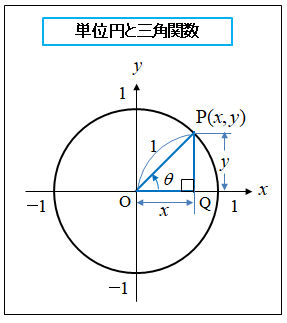
図のように、原点O を中心とする半径1 の円を 「単位円」 といいます。
直角三角形POQ で、角θに対する三角関数は、次のとおりです。
\(\cosθ=\cfrac{x}{OP}=\cfrac{x}{1}…x=\cosθ\)
\(\sinθ=\cfrac{y}{OP}=\cfrac{y}{1}…y=\sinθ\)
従って、P点の座標 (x,y) は (\(\cosθ,\sinθ\)) で表されます。
■ 特殊な角度の三角関数の値
★ 角度30°の場合
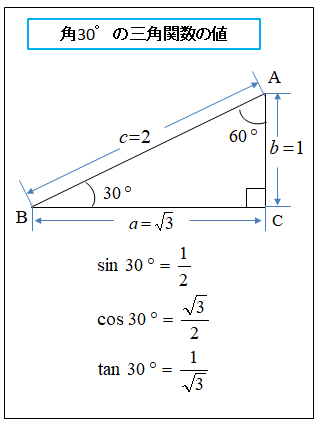
★ 角度60°の場合
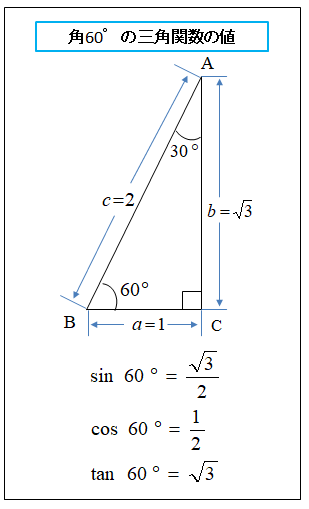
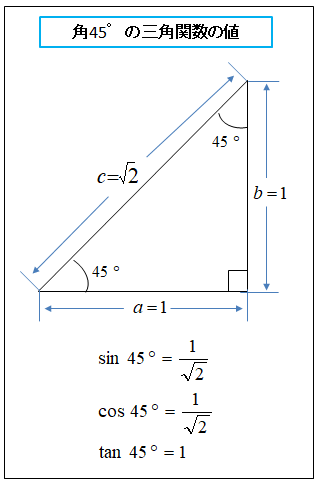
★ 角度45°の場合
■ 角度0°と角度90°の場合
角度が0° または90° のときの三角関数はどうなるか見て見ましょう。
図のような、半径が1 の単位円で角θの三角関数の値を調べます。
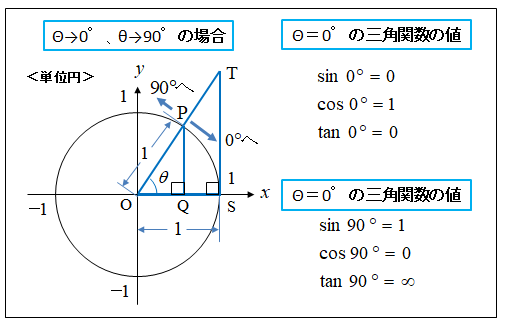
半径OP およびOS は1 であり、ΔPOS と ΔTOS は相似です。
\(\sinθ=\cfrac{PQ}{OP}=PQ\)
\(\cosθ=\cfrac{OQ}{OP}=OQ\)
\(\tanθ=\cfrac{TS}{OS}=TS\)
いま、\(θ\) が小さくなって、0 に近づくと
\(PQ→0\)
\(OQ→1\)
\(TS→0\)
従って
\(\sinθ=0\)
\(\cosθ=1\)
\(\tanθ=0\)
になります。
次に、\(θ\) が大きくなって、90° に近づくと
\(PQ→1\)
\(OQ→0\)
\(TS→∞\)
従って
\(\sinθ=1\)
\(\cosθ=0\)
\(\tanθ=∞\)
になります。
弧度法は角度の大きさを表す
■ 円の「弧」の長さと中心角との関係で角度を表すのが「弧度法」です。
図のように、半径の異なる円において、 半径と等しい弧の長さ に対する中心角θの大きさは、半径の長さに関係なく一定になります。
この角度θの大きさを 1ラジアン として、角度を表す方法を 弧度法 といい、単位として [rad](ラジアン)を用います。
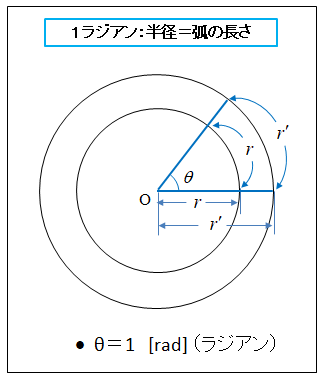
■ 中心角は弧の長さに比例する
図のように、半径 \(r\) の円において、長さ \(l\) 円弧に対する中心角 \(θ\) の大きさは、弧の長さに比例する。
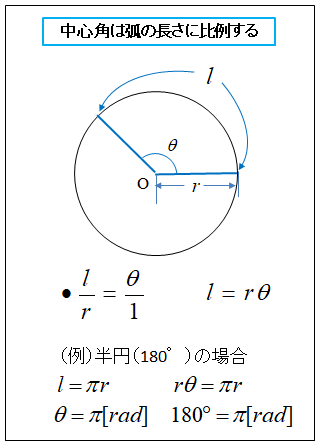
円の \(弧の長さl=半径r\) のときの角度は 1 [rad] です。
\(\cfrac{l}{r}=\cfrac{θ}{1}\)
\(l=rθ\)\(\cdots(1)\)
半円のときの中心角を \(θ\quad\rm[rad]\) とすると弧の長さ \(l\) は
\(l=πr\)\(\cdots(2)\)
式(2)を式(1)に代入すると
\(πr=rθ\)
\(θ=π\quad\rm[rad]\)
半円に対する中心角は 180° なので
\(180°=π\quad\rm[rad]\) となります。
非常に小さい角度の三角関数
■ Δtを非常に小さい時間とした場合の公式
Δtを非常に小さい時間とすると、次のようになります。
\(\cosωΔt≒\cos0=1\)
\(\sinωΔt≒ωΔt\)
★ 非常に小さい角度の三角関数の説明
いま、図のような半径1の円を考えるたとき
角度θラジアンに対する、円弧の長さはθ
sinθは 赤線の長さ
cosθは 青線の長さ になリます。
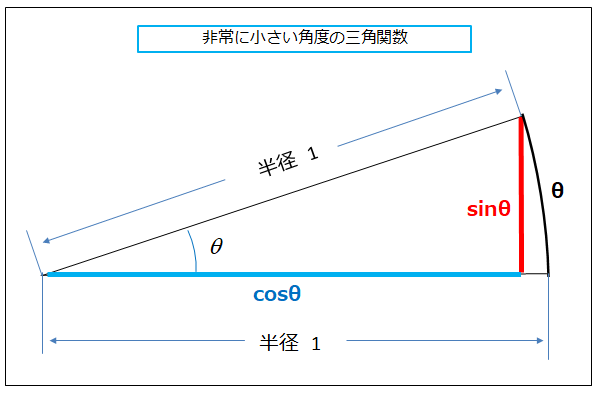
従って、角度θ の値が0(ゼロ)に近づいて行くと
\(θ→0\) のとき \(\sinθ→θ\)(赤線の長さは、円弧の長さに近づいて行く)
\(\cosθ→1\)(青線の長さは、円の半径の1に近づいて行く)
\(\tanθ→θ\)(\(\tanθ=\cfrac{\sinθ}{\cosθ}=\cfrac{θ}{1}=θ\))