正弦波交流の瞬時値と最大値

正弦波交流の瞬時値と最大値についての説明です。

正弦波交流はその時々で、大きさと向きが変わります。

正弦波交流のある時点での値を　瞬時値　といいます。

また瞬時値のうちで最大のものを　最大値　といいます。

正弦波交流の瞬時値の表わし方

■　瞬時値

正弦波交流起電力の瞬時値　\(e\)　の最大値を　\(E_m\)　実効値を　\(E\)　で表すと次のようになります。

\(e=E_m\sinωt\)　[V]

\(e=\sqrt{2}E\sinωt\)　[V]　

正弦波交流電流の瞬時値　\(i\)　を最大値　\(I_m\)　実効値を　\(I\)　で表すと次のようになります。

\(i=I_m\sinωt\)　[A]

\(i=\sqrt{2}I\sinωt\)　[A]　

■　最大値と実効値

最大値　と　実効値　の間には次のような関係があります。

最大値＝\(\sqrt2\)　実効値

\(E_m=\sqrt2E\)

\(I_m=\sqrt2I\)

実効値＝\(\cfrac{\rm 最大値}{\sqrt2}\)

\(E=\cfrac{E_m}{\sqrt2}\)

\(I=\cfrac{I_m}{\sqrt2}\)

正弦波交流の瞬時値とは、ある回転角における瞬時の値をいう

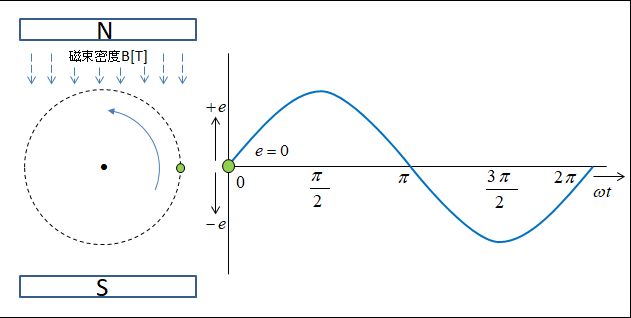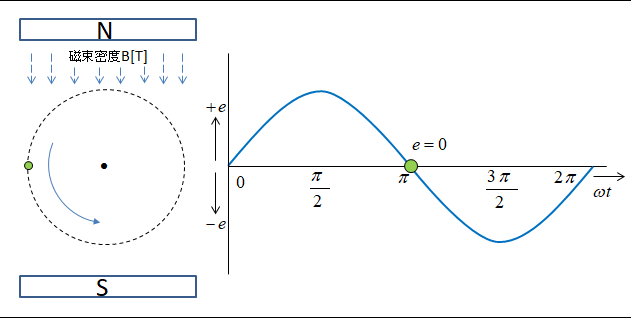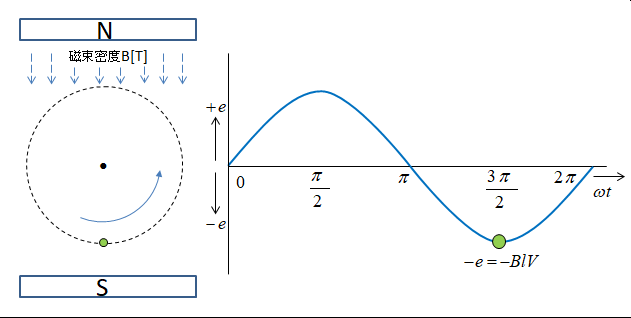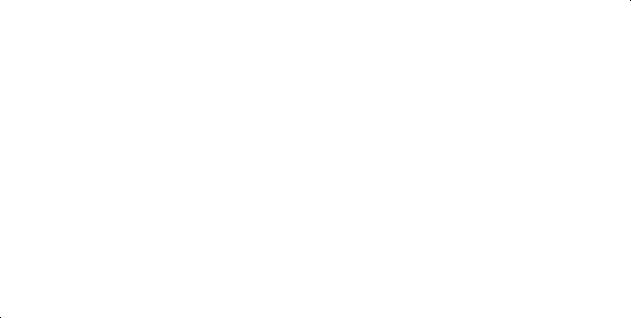
磁束密度　\(B\)　[T]　の平等磁界中を長さ　\(l\)　[m]　の導体が

速度　\(v\)　[m/s]　で等速円運動をしたときの誘導起電力 \(e\)　[V]　は次のようになります。

\(e=Blv\sinθ\)　[V]　

誘導起電力　\(e\)　[V]　は　導体の回転とともに回転角　\(ωt\)　[rad]　が変わるので、その瞬間の値は時間とともに変化します。

その瞬時の値のことを　瞬時値　といいます。

通常瞬時値は、起電力を　\(e\)、電流を　\(i\)　と小文字で表わします。

最大値とは瞬時値の中の最大の値をいう

■　瞬時値

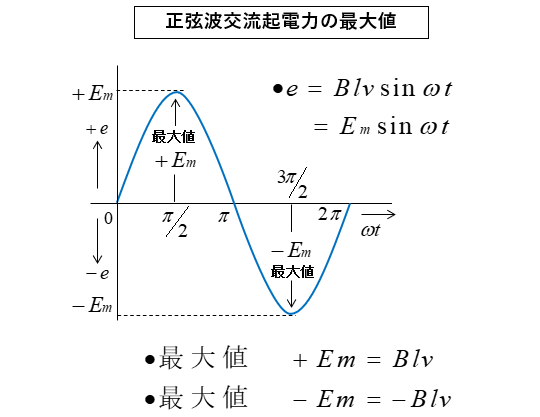
\(e=Blv\sinωt\)\(=E_m\sinωt\)

■　正弦波交流起電力

\(e=Blv\sinωt\)　（\(ωt=π/2\)）　とすると、

\(\sin\cfrac{π}{2}=1\)　なので

\(e=Blv\sin\cfrac{π}{2}\)\(=Blv=E_m\)　

\(Blv\)　が最大値 \(E_m\) となり

正の最大値　といいます。

\(ωt=3π/2\) のときが

\(e=-Blv\)　となり

負の最大値　といいます。

■　ピークピーク値

正弦波交流の正の最大値から負の最大値までを、ピークピーク値　\(E_{PP}\)　といいます。

\(E_{PP}=2E_m\)　[V]　

ピークピーク値＝2 × 最大値　[V]　になります。

■　瞬時値を最大値で表す

正弦波交流起電力の瞬時値　\(e\)　を最大値　\(E_m\)　で表すと

\(e=E_m\sinωt\)　になります。

また、正弦波交流電流の瞬時値　\(i\)　を最大値　\(I_m\)　で表すと

\(i=I_m\sinωt\)　になります。

以上で「正弦波交流の瞬時値と最大値」の説明を終わります。