磁束と磁束密度

磁束も　磁力線　も、どちらも　磁界の様子を表すための仮想的な線　です。

磁束は磁極　m　[Wb]　からは　m　[本]　の磁束が出ると考えます。

一方、磁力線は磁極　m　[Wb]　から　m/μ　[本]　の磁力線が出ると考えます。

磁束と磁力線の性質について説明します。

磁束

磁束　も　磁力線　も、どちらも磁界の様子を表すために考えた仮想的な線のことです。

磁力線というと１本づつの線のイメージですが、磁力線を束にしたものが　磁束　と考えれば良いでしょう。

■　磁束の記号と単位

磁束の記号は　\(\Phi\)　または　\(\phi\)　を使い、単位には　[Wb]　を使います。

\(\Phi、\phi\)　は「ファイ」、[Wb]　は「ウェーバー」と読みます。

磁束の定義

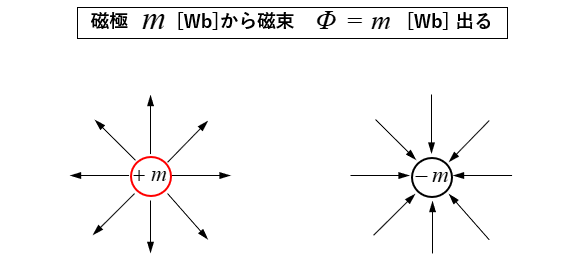
磁束を　\(\Phi\)、　磁束密度を　\(B\)、　面積を　\(S\)　とすると

\(\Phi=BS\)　[Wb]　になります。

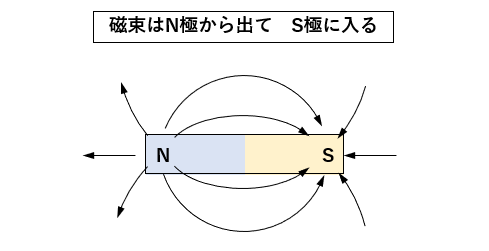
■　磁束　\(\Phi\)　は　N極から出て、S極に入る。

磁束は磁力線と同じように、N極から出て、S極に入る。

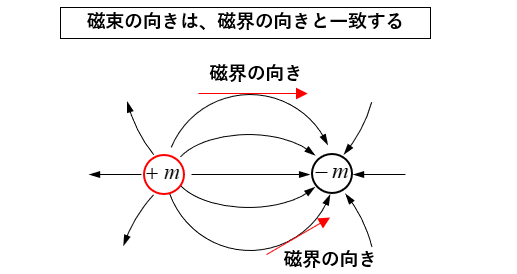
■　磁束　\(\Phi\)　の向き

磁束の向きは、その点の　磁界　の向きと一致する。

1. 磁束数は磁荷量と同じになります。
   磁荷　\(m\)　[Wb]　からは　\(\Phi=m\)　[Wb]　の磁束　が出る。
2. 磁束は　N極　から出て　S極　に入る。
3. 磁束の方向は、その点の磁界の方向と一致する。
4. 磁束は、途中で分岐したり、交差することはない。

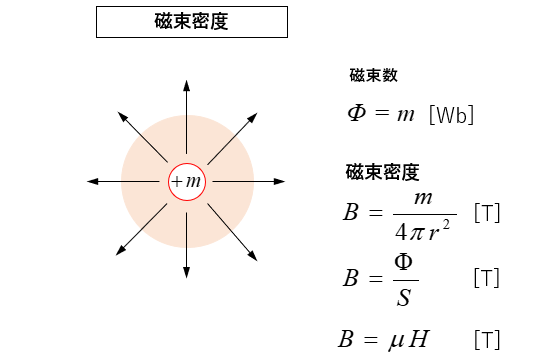
磁束密度

磁束密度　\(B\)　とは　単位面積あたりの磁束の数になります。

磁極　\(m\)　[Wb]　から　\(\Phi=m\)　[Wb]　の磁束　が球面状に出ますので

単位面積（１m²）　あたりの磁束数が磁束密度　\(B\)　[T]（テスラ）になります。

磁束密度は磁束　\(\Phi=m\)　を球の表面積　\(S=4πr^2\)　で割れば求められます。

\(B=\cfrac{m}{4πr^2}\)

\(B=\cfrac{\Phi}{S}\)

\(B=μH\)　[T]

磁界の強さ

\(H=k\cfrac{m}{r^2}=\cfrac{1}{4πμ}×\cfrac{m}{r^2}\)

\(=\cfrac{1}{μ}×\cfrac{m}{4πr^2}=\cfrac{1}{μ}×B\)

磁束密度

\(B=μH\)　[T]　になります。

磁束と磁力線の違い

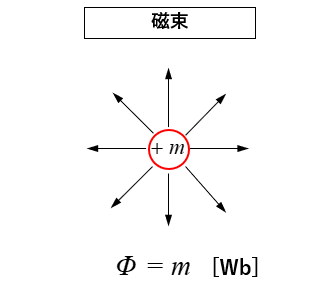
磁束数　\(\cdots\)　磁極　\(m\)　[Wb]　からは　\(\Phi=m\)　[Wb]　の磁束が出る。

磁束はどのような媒質中でも　透磁率の影響は受けない。

\(\Phi=m\)　[Wb]＝[本]

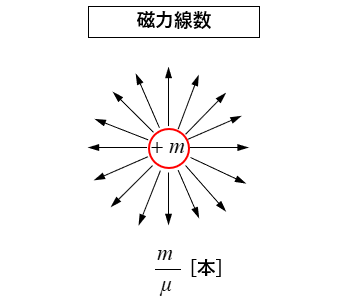
磁力線数　\(\cdots\)　磁極　\(m\)　[Wb]　からは　\(\cfrac{m}{μ}\)　[本]　の磁力線が出ます。

\(μ\)　は小さいので、磁力線の数はとても多くなります。

\(N=\cfrac{m}{μ}\)　[本]

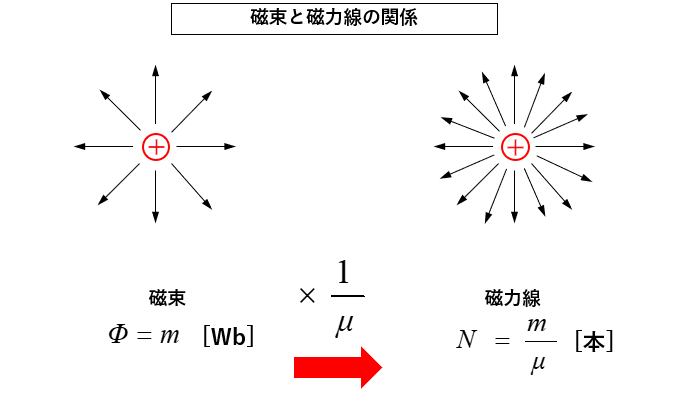
■　磁束と磁力線の関係

磁束と磁力線の関係は

磁束数を　\(\cfrac{1}{μ}\)　倍　したものが　磁力線数になります。

磁束の関係式

磁束数を　\(\Phi=m\)　[Wb]、　球の表面積を　\(S=4πr^2\)　[m²]　とします。　

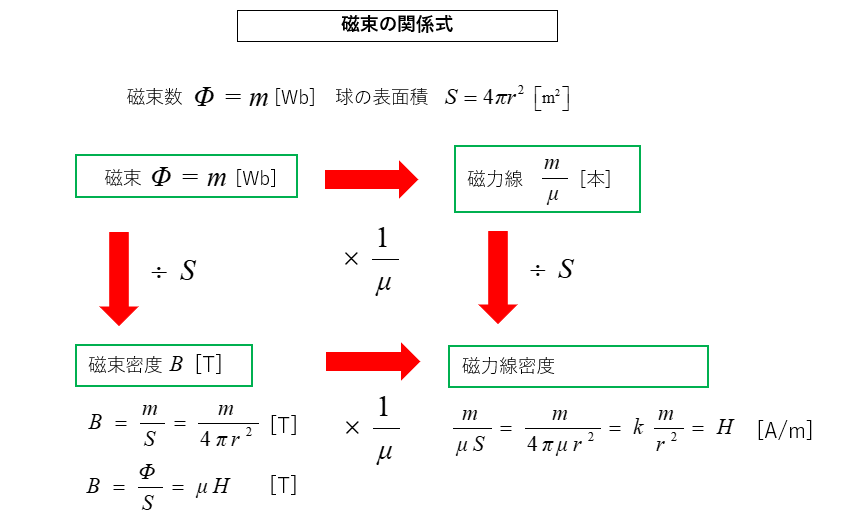
磁束数　\(\Phi=m\)　[Wb]　を　\(S=4πr^2\)　で割ると磁束密度　\(B\)　になります。

\(B=\cfrac{\Phi}{S}=\cfrac{m}{S}\)

\(=\cfrac{m}{4πr^2}×\cfrac{μ}{μ}\)

\(=k\cfrac{mμ}{r^2}=μH\)　[T]　

磁束密度を　\(μ\)　で割ると磁力線密度　になります。

磁力線密度　\(=\cfrac{m}{μS}=\cfrac{m}{4πμr^2}=H\)　で　磁界　になります

磁束数　\(m\)　[本]　を　\(μ\)　で割ると磁力線数　になります。

磁力線数　\(=\cfrac{m}{μ}\)　[本]　

磁力線数　\(=\cfrac{m}{μ}\)　[本]　を　\(S=4πr^2\)　で割ると磁力線密度　になります。

磁力線密度　\(=\cfrac{m}{μS}=\cfrac{m}{4πμr^2}=H\)　で　磁界　になります

以上で「磁束と磁束密度」の説明を終わります。