磁気回路と電気回路には、共通点があります。
磁気回路の起磁力、磁気抵抗を電気回路と比較して説明します。
磁気回路と電気回路の比較
磁気回路と電気回路を比較したものが次の表になります。
用語自体は違いますが、計算式などは似ている所があります。
🔳 磁気回路と電気回路の比較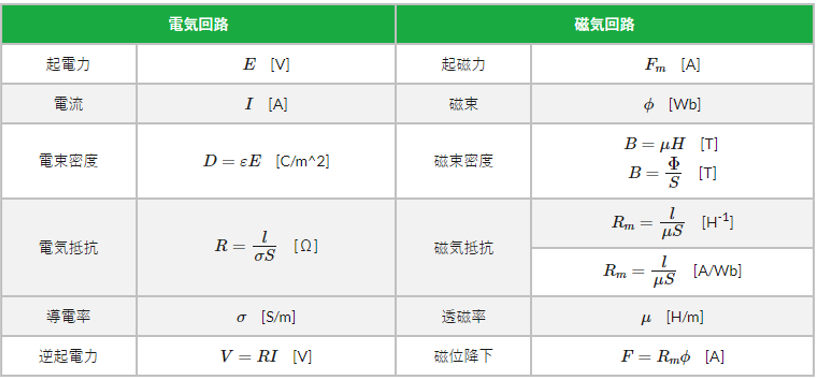
磁気回路
磁気回路の起磁力
磁気回路の鉄心にコイルを巻き、これに電流を流すと、鉄心中に磁束を生じます。
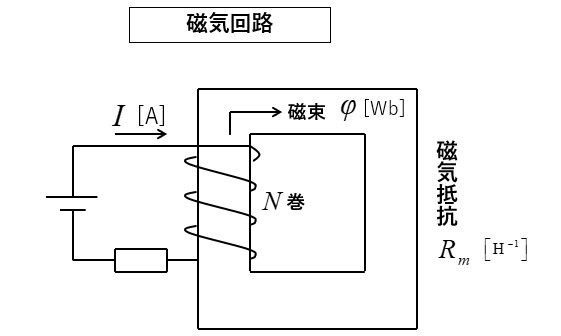
この時発生する磁束の量は、コイルの巻き数が多いほど、流れる電流が大きいほど多くなります。
この磁束の元になるものを磁気回路の起磁力 \(F_m\) [A] という。
\(F_m=NI\) [A]
磁気回路の磁気抵抗
磁気回路の起磁力を \(F_m=NI\) [A](アンペア)
磁束を \(\phi\) [Wb](ウェーバー)
磁気抵抗を \(R_m\) [H-1]=[1/H](毎ヘンリー)または [A/Wb] とすると
オームの法則のように、次の式になります。
\(R_m=\cfrac{NI}{\phi}\) [H-1]
磁気回路の磁気抵抗 \(R_m\) [H-1] は磁路の長さ \(l\) [m] に比例し
磁路の断面積 \(S\) [m2] に反比例する。
\(μ\)(ミュー)は透磁率で、単位は [H/m](ヘンリー毎メートル)
\(R_m=\cfrac{l}{μS}\) [H-1]
透磁率は磁気を通す比率を表します。
\(k=\cfrac{1}{4πμ_0}≒6.33×10^4\) [N・m2/Wb2]\(\cdots\)定数
\(μ_0=4π×10^{-7}\) [H/m]\(\cdots\)真空の透磁率
\(μ=μ_0μ_r\) [H/m]\(\cdots\)透磁率で「ミュー」と読みます。
\(μ_r=\cfrac{μ}{μ_0}\cdots\)比透磁率 空気中では、\(μ_r=1\) です。
\(k=\cfrac{1}{4πμ}\cdots\)透磁率\ (μ\) の媒質中の定数
磁気回路の磁束について
磁気回路の断面積を \(S\) [m2]
磁路の長さ \(l\) [m] の鉄心にコイル を \(N\) 回巻き
\(I\) [A] の電流を流した場合、鉄心の透磁率を \(μ\) とすると
生じる磁束 \(\phi\) [Wb] は次のようになります。
\(\phi=\cfrac{NI}{R_m}=\cfrac{NI}{\cfrac{l}{μS}}=\cfrac{μSNI}{l}\) [Wb]
\(μ=μ_0μ_r\quad\rm[H/m]\)
\(μ\):鉄心の透磁率
\(μ_0\):真空の透磁率
\(μ_r\):比透磁率
真空の透磁率
\(μ_o=4π×10^{-7}\) [H/m]
比透磁率
\(μ_r=\cfrac{μ}{μ_o}\)
鉄心を取り去った場合の磁束 \(\phi_o\) [Wb] は次のようになります。
\(\phi_o=\cfrac{μ_oSNI}{l}\) [Wb]
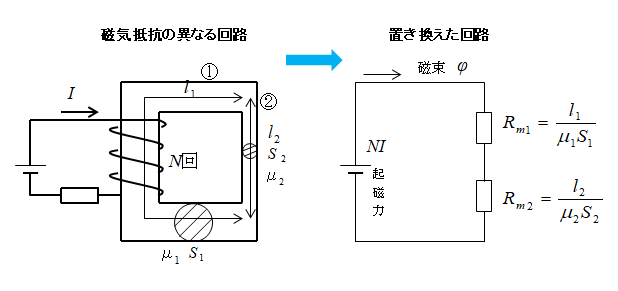
磁気抵抗が異なる回路の計算
磁気回路 ① と ② が接続されている。
それぞれの磁気回路の透磁率を \(μ_1、μ_2\) [H/m]
断面積を \(S_1、S_2\) [m2]、磁路長を \(l_1、l_2\) [m] とすると
磁気抵抗 \(R_m\) は次のようになる。
\(R_m=R_{m1}+R_{m2}\)\(=\cfrac{l_1}{μ_1S_1}+\cfrac{l_2}{μ_2S_2}\)
起磁力を \(F_m=NI\) [A] とすれば、磁束 \(\phi\) [Wb] は次のようになります。
\(F_m=NI\)\(=R_m×\phi=(R_{m1}+R_{m2})×\phi\) [A]
\(\phi=\cfrac{NI}{R_m}\)\(=\cfrac{NI}{R_{m1}+R_{m2}}\)\(=\cfrac{NI}{\cfrac{l_1}{μ_1S_1}+\cfrac{l_2}{μ_2S_2}}\) [Wb]
起磁力 \(NI\) は上の式より
\(NI\)\(=\cfrac{\phi l_1}{μ_1S_1}+\cfrac{\phi l_2}{μ_2S_2}\quad\rm[A]\)
磁束密度は \(B_1=\cfrac{\phi}{S_1}、B_2=\cfrac{\phi}{S_2}\) ですから
\(NI=\cfrac{B_1}{μ_1}l_1+\cfrac{B_2}{μ_2}l_2\) [A]
磁界の強さは \(H_1=\cfrac{B_1}{μ_1}、H_2=\cfrac{B_2}{μ_2}\) なので
\(NI\)\(=H_1l_1+H_2l_2\) [A]
図のように、一つの磁気回路において異なる磁気抵抗の場合は
磁気抵抗が直列に接続されているものと表すことができます。

磁気回路の主な用語
磁気回路の主な用語
起磁力\(\cdots\)\(F_m=NI\) [A]
磁気抵抗\(\cdots\)\(R_m=\cfrac{NI}{\phi}\) [A/Wb]=[1/H]=[H-1]
磁気抵抗\(\cdots\)\(R_m=\cfrac{l}{μS}\) [A/Wb]
真空の透磁率\(\cdots\)\(μ_o=4π×10^{-7}\) [H/m]
透磁率\(\cdots\)\(μ\) [H/m]
磁束\(\cdots\)\(\phi=\cfrac{NI}{R_m}=\cfrac{NI}{\cfrac{l}{μS}}=\cfrac{μSNI}{l}\) [Wb]
比透磁率\(\cdots\)\(μ_r=\cfrac{μ}{μ_o}\)
磁気抵抗の異なる回路の計算\(\cdots\)\(R_m=R_{m1}+R_{m2}=\cfrac{l_1}{μ_1S_1}+\cfrac{l_2}{μ_2S_2}\)
磁束密度\(\cdots\)\(B=\cfrac{\phi}{S}\) [T]=[Wb/m2]=[N/A・m]\)
磁界の強さ\(\cdots\)\(H=\cfrac{B}{μ}\) [A/m]
起磁力\(\cdots\)電気回路の電源(電池)にあたるもの。
磁束\(\cdots\)電気回路の電流にあたるもの。
磁束密度\(\cdots\)単位面積当たりの磁束の量
磁気抵抗\(\cdots\)電気回路の抵抗にあたるもの。
以上で「磁気回路」の説明を終わります。
