磁界 は目に見えないので、理解しづらいものです。
そこで、磁界の様子を表すための 仮想的な線 を考えました。
それが 磁力線 です。
ここでは、磁力線と磁力線密度について説明します。
磁力線
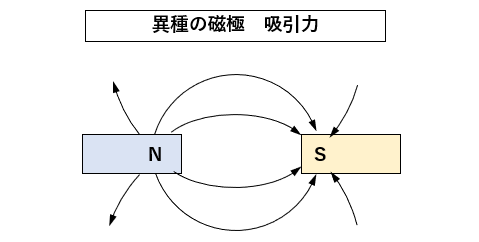
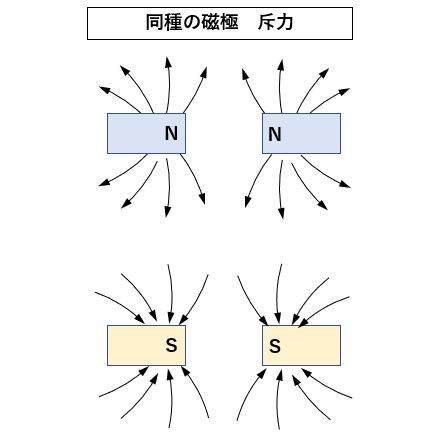
吸引力と斥力
磁力線は N極 から出発して S極 に入ります。
異種の磁極同士 が近くにある場合、吸引力が働きます。
同種の磁極同士 が近くにある場合、斥力が働きます。
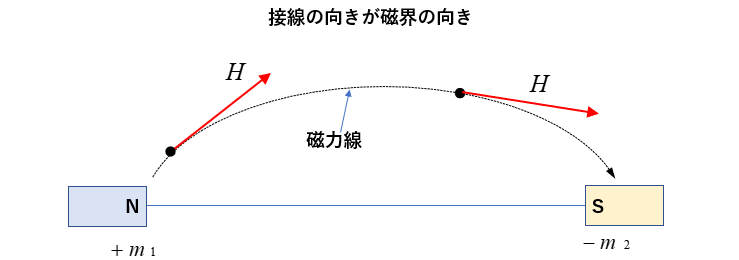
■ 磁界の向き
図のように、磁力線の接線の向きが磁界の向きになる。
■ 磁力線と方位磁針
磁界の中に方位磁針を置くと、方位磁針は図のような向きになります。

- N極から出て、S極に入る。
- 途中で交わったり、枝分かれしたりしない。
- 接線の向きが磁界の向きになる。
- 磁力線密度は、磁界の強さを表します。
磁力線の本数
磁界の強さ \(H\) の面において
単位面積当たり \(H\) 本 の磁力線が直角に貫くと決めます。
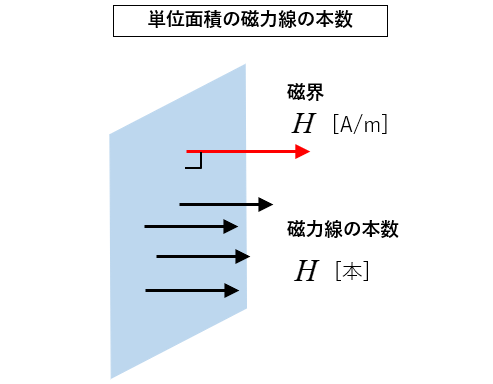
磁力線の本数
磁力線の本数の定義
磁界の強さ \(H\) に対して垂直な 単位面積 1m2 を貫く磁力線の本数を \(H\) 本 と決める。
磁極から出る磁力線の総本数 \(N\) は 次のようになります。
\(N=4πkm\) [本]
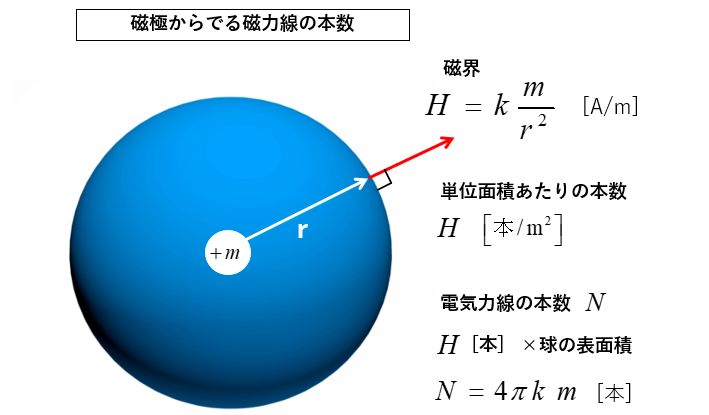
図において
磁極 \(m\) から \(r\) の磁界の強さは
\(H=k\cfrac{m}{r^2}\) です。
単位面積あたりの磁力線の本数は
\(H\) [本/m2] なので
磁力線の総本数 \(N\) は、球の表面積を掛ければ求められます。
\(N=H×4πr^2=4πkm\) [本] \(\cdots (1)\)
定数 \(k\) は
\(k=\cfrac{1}{4πμ}\) \(\cdots (2)\)
式(2)を 式(1)へ代入すると
\(N=\cfrac{m}{μ}\) [本] になります。
透磁率は磁気を通す比率を表します。
\(k=\cfrac{1}{4πμ_0}≒6.33×10^4\) [N・m2/Wb2]\(\cdots\)定数
\(μ_0=4π×10^{-7}\) [H/m]\(\cdots\)真空の透磁率
\(μ=μ_0μ_r\) [H/m]\(\cdots\)透磁率で「ミュー」と読みます。
\(μ_r=\cfrac{μ}{μ_0}\cdots\)比透磁率 空気中では、\(μ_r=1\) です。
\(k=\cfrac{1}{4πμ}\cdots\)透磁率 \(μ\) の媒質中の定数
磁力線密度
磁極 \(m\) からは \(N=4πk m\) [本] の磁力線が出ています。
磁力線密度 [本/m2] は単位面積あたりの磁力線の本数です。
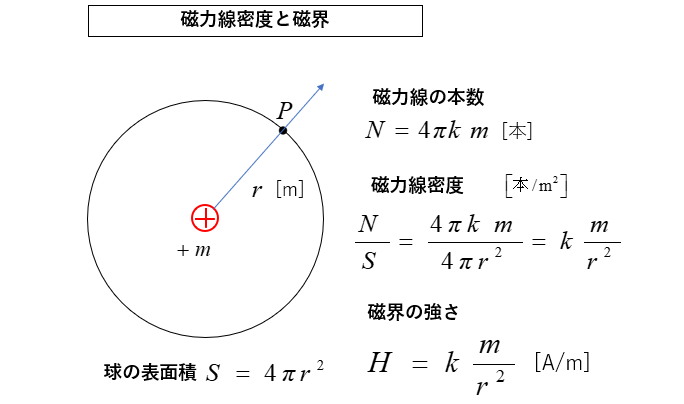
磁力線の定義から 単位面積あたりの磁力線の本数は磁界の強さ \(H\) になります。
磁力線密度 [本/m2] = 磁界の強さ \(H\) [A/m] になります。
磁力線の総数を球の面積 \(4πr^2\) で割ると 磁界の強さ になります。
磁力線密度\(=\cfrac{1}{4πr^2}×\cfrac{m}{μ}\)
\(=\cfrac{m}{4πμr^2}=\)磁界の強さ \(H\) になります。
以上で「磁力線と磁力線密度」の説明を終わります。
