導体に電流が流れると導体の周りに磁界が発生します。
電流が流れたときに発生する磁界には
直線電流による磁界、円形コイルによる磁界、無限長ソレノイドによる磁界、環状ソレノイド による磁界があります。
2本の無限長直線状導体の間には力が働きます。
ここでは、電流が作る磁界について説明します。
直線電流による磁界
右ねじの法則
🔳 導体に電流が流れると、導体の周りに磁界が発生することはよく知られています。
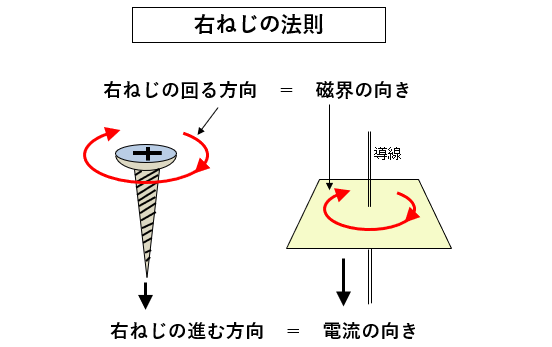
導体に電流が流れたときにできる磁界の向きは
右ねじの法則(アンペールの右ねじの法則) による磁界ができます。
直線電流による磁界
🔳 無限長の直線導体に電流が流れると 導体の周囲に円形の磁界 ができます。
磁界 \(H\) の方向は円周に対して 接線の方向 になります。
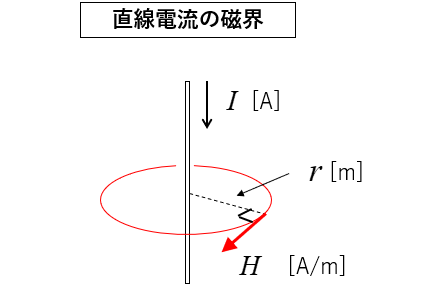
直線導体に流れる電流を \(I\) [A]
導体から \(r\) [m] 離れた
円周上の 磁界の強さ \(H\) [A/m] は次の式になります。
\(H=\cfrac{I}{2πr}\) [A/m]
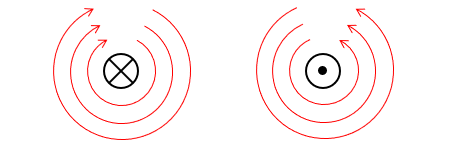
■ 平面図を描く記号
電流などの方向を平面で表示する記号です。

🔳 磁界は右ねじの法則に従って 直線導体に対して 同心円状 にできます。
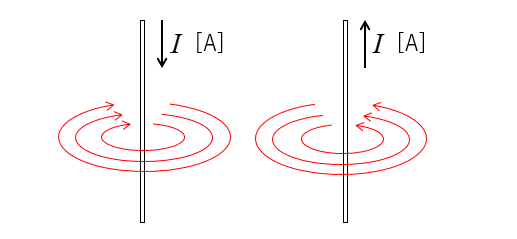
🔳 上図を上から見て平面的に描くと、次のようになります。
円形コイルが中心に作る磁界
1回巻きの円形コイルに電流が流れると
右ねじの法則による直線上の磁界が コイルの中心 にできます。

コイルの半径を \(r\) [m]
電流を \(I\) [A] とすると
磁界の強さ \(H\) [A/m] は次のようになります。
\(H=\cfrac{I}{2r}\) [A/m]
🔳 円形コイルの微小な一部を考えると
直線電流と同じように右ねじの法則の磁界が発生します。
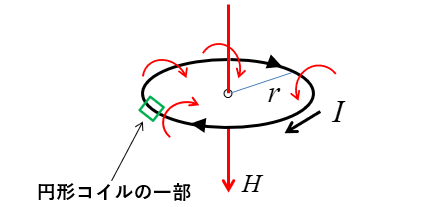
この公式で求めることができるのは円の中心の磁界だけです。
図の「×」にあるように
中心から少しずれた位置や円の直線上の他の点の磁界は求められません。
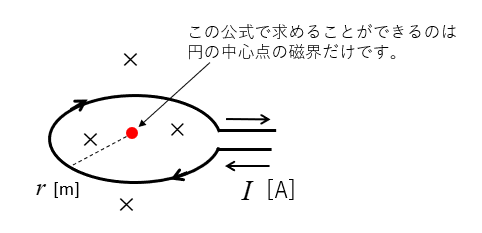
コイルの巻数が N 巻の場合
円形コイルが \(N\) 巻の場合の
円形コイルの中心の磁界の強さは、次のようになります。
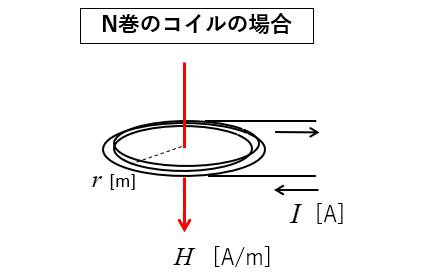
\(H=\cfrac{NI}{2r}\) [A/m]
2本の無限長直線状導体の間に働く力
■ 2本の無限長直線状導体の間に働く力
平行な2本の無限長直線状導体の間には力が働きます。
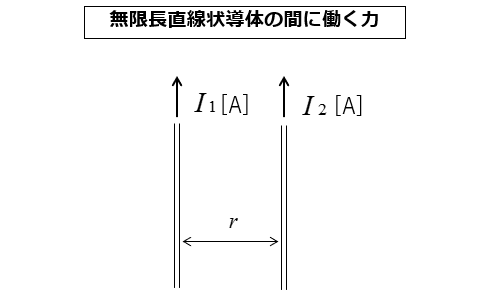
★ 2本の無限長直線状導体の間に働く \(1\) [m] 当たりの力 \(F\) [N/m] は次のようになります。
\(F=\cfrac{μI_1I_2}{2πr}\) [N/m]
\(F=\cfrac{2I_1I_2}{r}×10^{-7}\) [N/m]
透磁率\(\cdots\)\(μ=4π×10^{-7}\) [H/m]
導体に流れる電流\(\cdots\)\(I_1、I_2\) [A]
導体間の距離\(\cdots\)\(r\) [m]
■ 力の向きは電流の向きが 同方向ならば吸引力 になります。
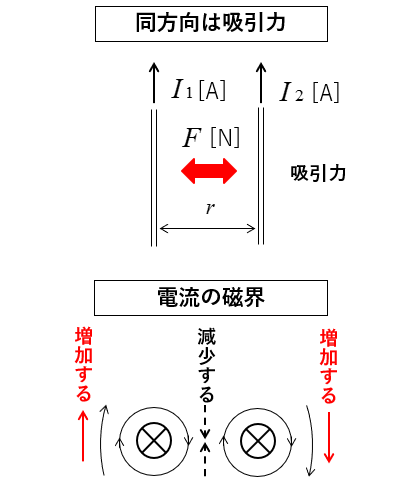
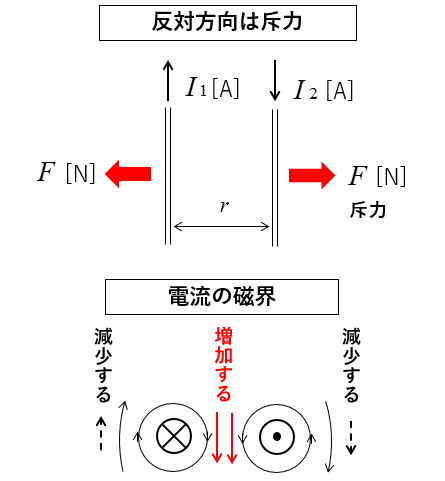
■ 力の向きは電流の向きが 反対方向の場合は斥力(反発力) になります。
無限長ソレノイドが作る内部磁界<
🔳 ソレノイドは、導線をグルグルと円筒状に巻いたコイルのことです。
ソレノイドの磁界の様子は 棒磁石のようになっていますので、電磁石とも呼ばれます。
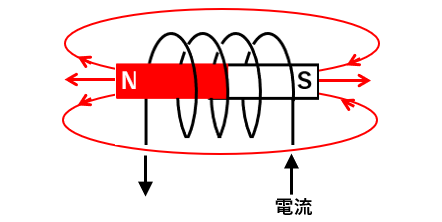
🔳 無限長ソレノイドでは、磁界は コイルの内側 にだけ発生します。
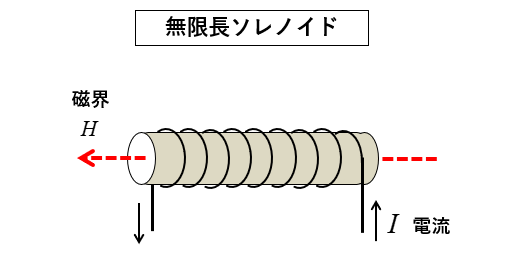
コイルの長さを無限長 \(l\) [m]
巻数を \(N\) 回 巻いたソレノイドで、電流 \(I\) [A] を流したとき
磁界の強さは次のようになります。
\(Hl=NI\) [A] (磁界の強さ×磁路の長さ=電流の総和)
内部磁界の強さ \(H\) [A/m] は
\(H=\cfrac{NI}{l}\) [A/m]
また、ソレノイド \(1\) m当たりの巻数を \(n\) とすると
\(n=\cfrac{N}{l}\) ですから
\(H=nI\) [A/m]
巻数 \(N\) と 巻数の密度 \(n\)
★ 無限長ソレノイドの \(N\)
無限長ソレノイドの \(N\) は巻数そのままの数になります。
つまり、100回巻いたとき \(N=100\) になります。
🔳 ソレノイドの \(n\)
これに対して、無限長ソレノイドの、\(n\) は巻数の密度を表わしています。
つまり、1m 当たりの巻数になので
もし、2m 当たりで100 回ならば \(n=50\) になるのです。
また、ソレノイドの場合は、半径 \(r\) がなくなっていることに注意が必要です。
環状ソレノイドが作る内部磁界
図のような、環状ソレノイドでは内部だけに磁界が発生します。
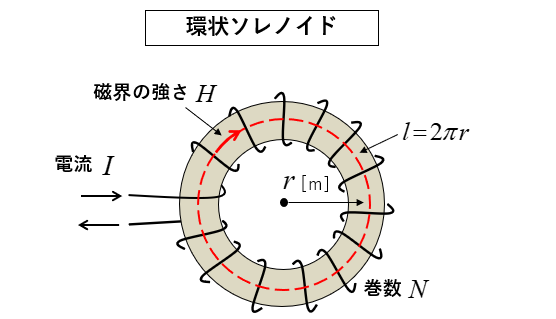
巻数が \(N\) 回巻きの環状ソレノイドに
電流 \(I\) [A] を流したとき、半径 \(r\) [m] とすると
磁路の長さは \(l=2πr\) [m] なので
\(Hl=NI\) [A] (磁界の強さ×磁路の長さ=電流の総和) になります。
\(H=\cfrac{NI}{l}=\cfrac{NI}{2πr}\) [A/m] となります。
公式のまとめ
■ 直線電流の磁界
\(H=\cfrac{I}{2πr}\) [A/m]
■ 円形コイルが中心に作る磁界
\(H=\cfrac{I}{2r}\) [A/m]
■ N巻の円形コイルが中心に作る磁界
\(H=\cfrac{NI}{2r}\) [A/m]
■ 2本の無限長直線状導体の間に働く力
\(F=\cfrac{μI_1I_2}{2πr}\) [N/m]
■ 無限長ソレノイドが作る内部磁界の強さ
\(H=\cfrac{NI}{l}\) [A/m]
\(H=nI\) [A/m]
■ 環状ソレノイドが作る内部磁界の強さ
\(H=\cfrac{NI}{l}=\cfrac{NI}{2πr}\) [A/m]
練習問題
問題1
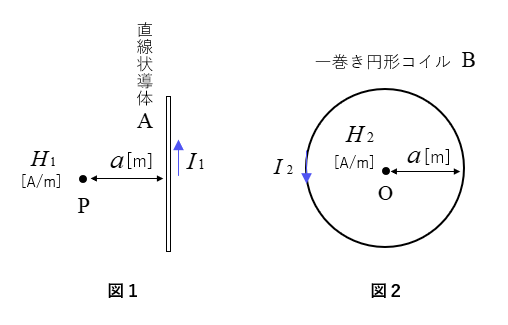
図1のように、無限長の直線上導体A に直流電流 \(I_1\) [A] が流れている時
この導体から \(a\) [m] の点P の磁界の大きさは \(H_1\) [A/m] でした。
一方、図2のように半径 \(a\) [m] の一巻きの円形コイルB に
直流電流 \(I_2\) [A] が流れている時
この円の中心点O の磁界の大きさは \(H_2\) [A/m] でした。
\(H_1=H_2\) である時の \(I_1\) と \(I_2\) の関係式を \(I_1\) の式で求めよ。
<解答例>
直線上導体A の点P の磁界の強さは、次のようになります。
\(H_1=\cfrac{I_1}{2πa}\)
一巻きの円形コイルB の点O の磁界の強さは、次のようになります。
\(H_2=\cfrac{I_2}{2a}\)
問題文から、\(H_1=H_2\) なので
\(\cfrac{I_1}{2πa}=\cfrac{I_2}{2a}\)
\(I_1=\) とすると
\(I_1=πI_2\) になります。
問題2
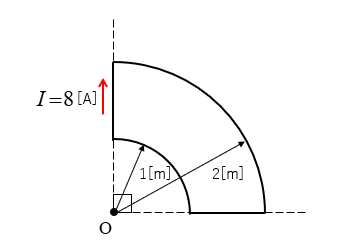
図のような、半径 1m と半径 2m の円形導線の
\(\cfrac{1}{4}\) の扇形導線がある。
この導線に図のような向きに直流電流 \(I=8\) [A] を流したとき
点O における磁界の強さを求めよ。
<解答例>
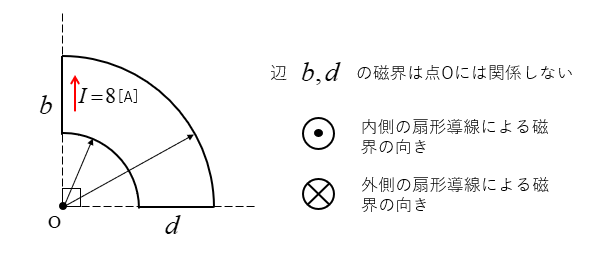
図のように、直線部の辺をb,dとすると
辺b,dの磁界は点Oには関係しませんので無視します。
円形電流の磁界の強さは
\(H=\cfrac{I}{2a}\) [A/m] ですが
問題は \(\cfrac{1}{4}\) の扇形導線です。
内側の扇形導線の磁界を \(H_1\) とすると
\(H_1=\cfrac{8}{2×1}×\cfrac{1}{4}=1\) [A/m]
外側の扇形導線の磁界を \(H_2\) とすると
\(H_2=\cfrac{8}{2×2}×\cfrac{1}{4}=\cfrac{1}{2}\) [A/m]
内側と外側の磁界の向きは逆向きなので
合成磁界 \(H\) は次のようになります。
\(H=H_1-H_2=1-\cfrac{1}{2}=0.5\) [A/m] になります。
磁界の向きは、奥から手前の向きになります。
問題3
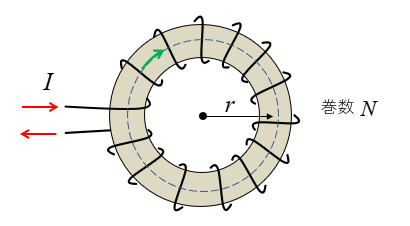
真空中に図のような環状ソレノイドがあります。
巻数 \(N=1000\) 電流 \(I=200\) [mA] 半径 \(r=40\) [mm] であるとき
図の一点鎖線上の磁束密度 \(B\) [T] を求めよ。
ただし、\(μ_0=4π×10^{-7}\) とする。
<解答例>
環状ソレノイドの内部磁界の強さは
\(H=\cfrac{NI}{l}=\cfrac{NI}{2πr}\) [A/m]
磁束密度 \(B\) は、\(B=μH\) より
\(B=μH=μ_0μ_rH\)\(=\cfrac{_0μ_rNI}{2πr}\) [T]
数値を代入して計算すると
\(B=\cfrac{4π×10^{-7}×1000×200×10^{-3}}{2π×4×10^{1-3}}\)
\(=1×10^{-3}\) [T] になります。
以上で「電流が作る磁界の強さ」の説明を終わります。
