磁界の中を荷電粒子が移動すると、磁界に影響されて荷電粒子には力が加わります。
このように磁界中を移動する荷電粒子に掛かる力のことを ローレンツ力 といいます。
また、電荷が移動するということは、電流が流れることになります。
磁界と荷電粒子が水平方向の場合は ローレンツ力は生じません。
荷電粒子が磁界を横切るときにだけ ローレンツ力が生じます。
ここでは、ローレンツ力と円運動について説明します。
ローレンツ力とは
🔳 図のように 磁界中 \(B\) を
荷電粒子 \(q\) が 移動 \(v\) すると 力 \(F\) を生じます。
この力 \(F\) を ローレンツ力 といいます。
荷電粒子とは電荷が 帯電 した粒子のことです。

ローレンツ力の大きさ \(F\) は、次の式で表されます。
\(F=qvB\) [N]
磁束密度\(\cdots\)\( B\) [T]
荷電粒子\(\cdots\)\(q\) [C]
荷電粒子の移動速度\(\cdots\)\(v\) [m/s]
ローレンツ力の方向
ローレンツ力の方向は フレミングの左手の法則 により知ることができます。
図のように、プラスの電荷が移動したということは
移動した方向に 電流 が流れたと考えることができます。
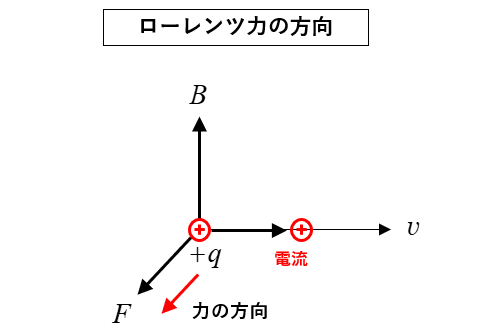
フレミングの左手の法則の電磁力
図のような磁界中の導体に電流が流れると
フレミングの法則の電磁力は奥から手前の力を受けます。
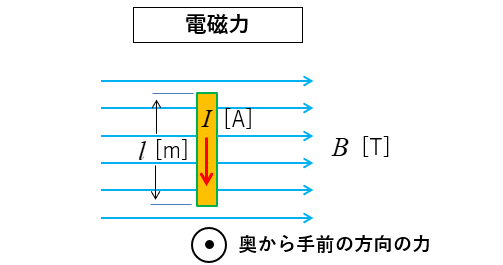
フレミングの法則の電磁力
フレミングの法則の電磁力 \(F\) は次のようになります。
\(F=BIl\) [N]
磁束密度\(\cdots\)\(B\) [T]
電流\(\cdots\)\(I\) [A]
導体の長さ\(\cdots\)\(l\) [m]
ローレンツ力と電磁力は等しい
ローレンツ力と 電磁力 は等しいので、次の式が成り立ちます。
\(F=qvB=BIl\) [N]
\(v=\cfrac{Il}{q}\) [m/s]\(\cdots (1)\)
電流の定義は
\(I=\cfrac{Q}{t}\) ですから
\(Q=It\)
式(1)に \(Q=It\) を代入します。
\(v=\cfrac{Il}{It}=\cfrac{l}{t}\)
\(v=\cfrac{l}{t}\) [m/s] となります。
荷電粒子とローレンツ力
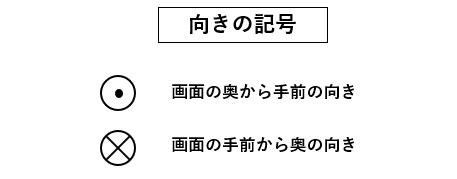
🔳 図は平面における磁界や電流などの向きを表示する記号です。
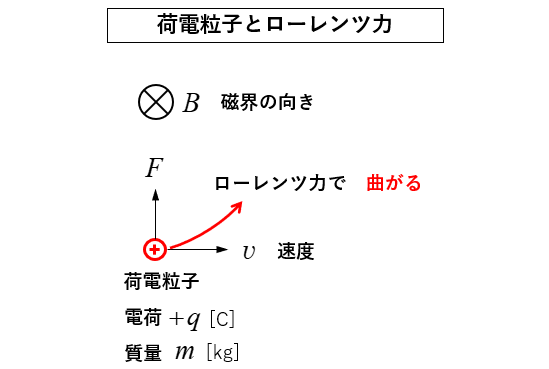
🔳 荷電粒子に 初速度 \(v\) を与えます。
荷電粒子は ローレンツ力 を受けて上向きの力を受けて 曲がり ます。
🔳 荷電粒子に速度 \(v\) が連続して加わると 等速円運動 になります。
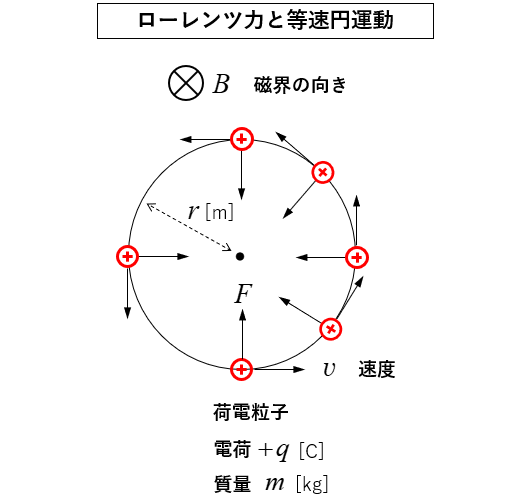
荷電粒子の電荷を \(q\) 初速度を \(v\) 質量を \(m\) とすると
ローレンツ力は
\(F=qvB\)
等速円運動の半径を \(r\) とすると
向心力は
\(F=\cfrac{mv^2}{r}\) になります。
ロレンツ力と向心力は等しくなるので
\(F=qvB=\cfrac{mv^2}{r}\)
等速円運動の半径 \(r\) は
\(r=\cfrac{mv}{qB}\) [m] になります。
ローレンツ力が荷電粒子に働く方向
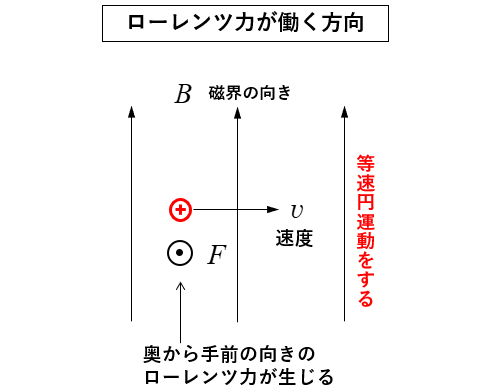
🔳 荷電粒子の移動の向きと磁界の向きが垂直の 場合は
図のような力を生じるので等速円運動をします。
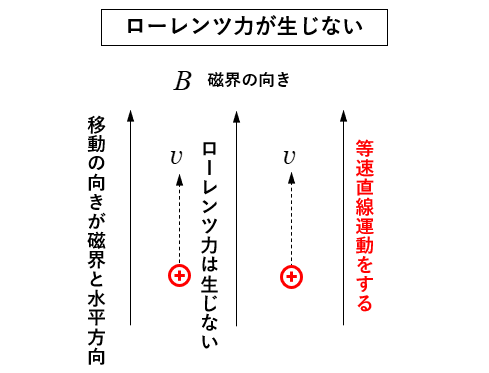
🔳 荷電粒子の移動の向きと磁界の向きが同じ 場合は
ローレンツ力が生じないので 等速直線運動 をします。
電子の等速円運動
電子が初速度 \(v\) で磁界中に突入すると
ローレンツ力 により電子は常に運動方向と直角の向きの力を受けます。
磁束の向きは 奥から手前 の時
電子に図のような初速度 \(v\) を加えると
電子はローレンツ力を受けて 等速円運動 になります。
電子が図のように動くことは
反対方向に電流 \(I\) が流れることと同じと考えることができます。
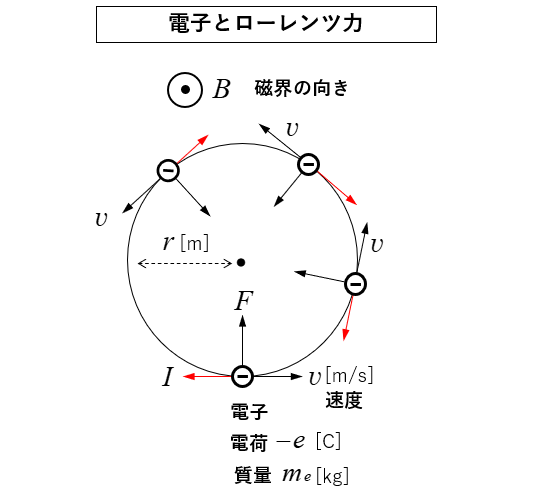
電子が受けるローレンツ力の大きさは
\(F=evB\) [N] になります。
向心力は
\(F=\cfrac{m_ev^2}{r}\) [N]
ローレンツ力と向心力は等しいので
\(F=evB=\cfrac{m_ev^2}{r}\) [N]
等速円運動の半径 \(r\) は
\(r=\cfrac{m_ev}{eB}\) [m] になります。
まとめ
🔳 フレミングの法則の電磁力
\(F=BIl\) [N]
磁束密度\(\cdots\)\(B\) [T]
電流\(\cdots\)\(I\) [A]
導体の長さ\(\cdots\)\(l\) [m]
🔳 荷電粒子 \(q\) が受けるローレンツ力
\(F=qvB\) [N]
磁束密度\(\cdots\)\( B\) [T]
荷電粒子\(\cdots\)\(q\) [C]
荷電粒子の移動速度\(\cdots\)\(v\) [m/s]
🔳 向心力の大きさ
\(F=\cfrac{mv^2}{r}\) [N]
🔳 ローレンツ力=向心力
\(F=qvB=\cfrac{mv^2}{r}\) [N]
🔳 荷電粒子の等速円運動の半径
\(r=\cfrac{mv}{eB}\) [m]
🔳 電子が受けるローレンツ力
\(F=evB\) [N]
磁束密度\(\cdots\)\( B\) [T]
電子の電荷\(\cdots\)\(-e\) [C]
電子の移動速度\(\cdots\)\(v\) [m/s]
🔳 向心力 の大きさ
\(F=\cfrac{m_ev^2}{r}\) [N]
🔳 ローレンツ力=向心力
\(F=evB=\cfrac{m_ev^2}{r}\) [N]
🔳 電子の円運動の半径
\(r=\cfrac{m_ev}{eB}\) [m]
以上で「ローレンツ力と円運動」の説明を終わります。
