電気に直流と交流があることは、誰でも知っていることでしょう。
直流は乾電池などで馴染みがあるので、よく知っていると思います。
直流は 電圧の大きさが一定で、電流の流れる向きも同じ方向 です。
しかし、交流の場合は 時間とともに電圧の大きさと向きが変化 します。
ここでは、交流の実効値について説明します。
正弦波交流の実効値の考え方
■ 実効値とは
図のように、同じ大きさの抵抗に直流電流と、交流電流を流したとします。
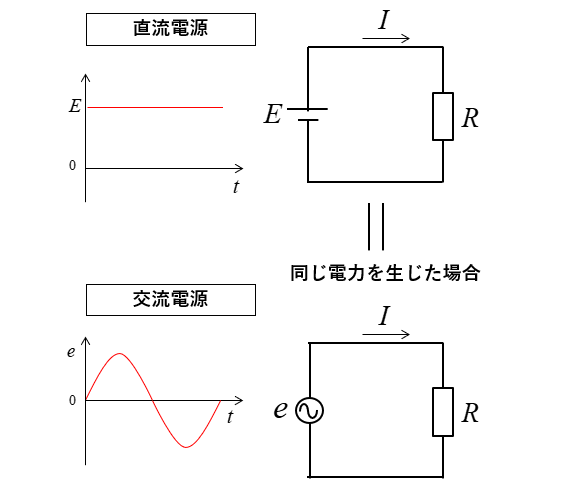
このときの電力量(仕事量)が同じになった場合、このときの交流の大きさを直流の値で表わします。
このときの値を 交流の実効値 とします。
交流電圧 \(e\) を 直流電圧の大きさ \(E\) で表わします。
交流の実効値を求める
正弦波交流電流 \(i\) と同じ効力の直流電流 \(I\) を求める。
下図の直流電源による電力を \(P_D\) とすると、次のようになります。
\(P_D=I^2R\) [W] \(\cdots(1)\)
また、交流電源による電力を \(P_A\) とすると、次のようになります。
\(P_A=i^2R\) [W] \(\cdots(2)\)

正弦波交流の電流は \(i=I_m\sinωt\) なので、時間の経過とともに大きさと流れる向きが変わります。
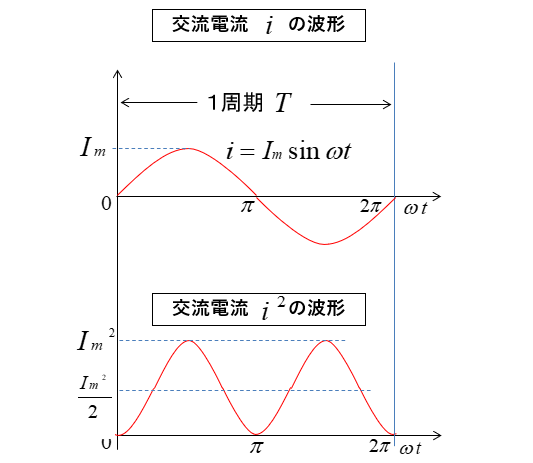
交流の場合は1周期が、繰り返されているわけですから、交流電源による電力 \(P_A\) を次のように表わします。
\(P_A=(i^2 \rm の1周期の平均値)×R\cdots(3)\)
そして \(P_D=P_A\) と仮定したのですから
式(1)と式(3)から
\(I^2R=(i^2 \rm の1周期の平均値)×R\)
\(I^2=(i^2 \rm の1周期の平均値)\)
\(I=\sqrt{(i^2 \rm の1周期の平均値)}\)

\(i=I_m\sinωt\) [A] の 2乗 の波形は周期的に変化し
負の電流の値も 2乗 されるので、すべてプラス(+)になります。
正弦波交流電流の実効値を求める
ここで、交流電流 \(i\) の実効値の値を求めてみます。
まず、\(i^2\) を求めると
\(i^2=(I_m\sinωt)^2\)
\(i^2={I_m}^2\sin^2ωt\cdots(4)\)
三角関数の 2倍角の公式から
\(\cos2α=1-2\sin^2α\)
\(\sin^2ωt=\cfrac{1-\cos2ωt}{2}\cdots(5)\)
式(4)に式(5)を代入すると
\(i^2={I_m}^2×\cfrac{1-\cos2ωt}{2}\)
\(i^2=\cfrac{{I_m}^2}{2}-\cfrac{{I_m}^2}{2}\cos2ωt\)\( \cdots(6)\)
■ cos2ωtの波形
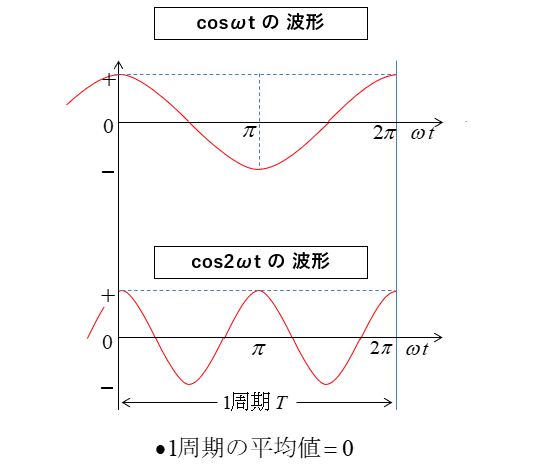
\(\cos2ω\) の波形は 1 周期を平均すると、正の波形と負の波形の面積が等しいので、0(ゼロ)です。
式(6)は
\(i^2=\cfrac{{I_m}^2}{2}-\cfrac{{I_m}^2}{2}\cos2ωt\)
\(-\cfrac{{I_m}^2}{2}\cos2ωt=0\) となるので
\(i^2\)\(=\cfrac{{I_m}^2}{2}-\cfrac{{I_m}^2}{2}\cos2ωt\)\(=\cfrac{{I_m}^2}{2}\)
実効値は次のようになります。
\(I=\sqrt{\cfrac{{I_m}^2}{2}}\)
\(I=\cfrac{I_m}{\sqrt2}\)\(\cdots(7)\)
従って 実効値は最大値の \(\cfrac{1}{\sqrt2}\) になります。
実効値と最大値と平均値の関係
実効値を \(E、I\)
最大値を \(E_m、I_m\)
平均値を \(E_{av}、I_{av}\) とします。
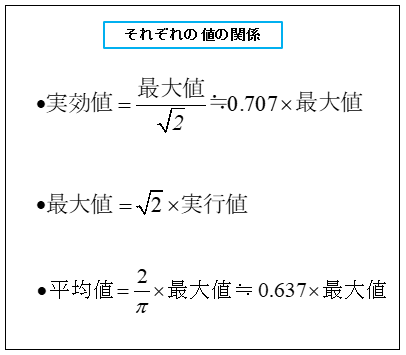
■ 実効値=\(\cfrac{\rm 最大値}{\sqrt2}\)\(≒0.707 × \rm 最大値\)
電圧の実効値 \(E=\cfrac{E_m}{\sqrt2}\) [V]
電流の実効値 \(I=\cfrac{I_m}{\sqrt2}\) [A]
■ 最大値=\(\sqrt{2}\) × 実効値
電圧の最大値 \(E_m=\sqrt{2}E\) [V]
電流の最大値 \(I_m=\sqrt{2}I\) [A]
■ 平均値=\(\cfrac{2}{π}\)× 最大値≒0.637×最大値
電圧の平均値 \(E_{av}=\cfrac{2}{π}×E_m\) [V]
電圧の平均値 \(I_{av}=\cfrac{2}{π}×I_m\) [A]
以上で「正弦波交流の実効値とは」の説明を終わります。