アドミタンスは、交流回路における電流と電圧の比です。インピーダンスは、交流回路における電圧と電流の比です。
アドミタンスとインピーダンスは、逆数の関係にあります。アドミタンスは、交流回路の電流の流れやすさを表し、インピーダンスは、交流回路の電流の流れにくさを表します。
この記事は、アドミタンスを構成する要素やアドミタンスの求め方について、わかりやすく解説します。
アドミタンスの記号や単位

アドミタンスの記号は \(Y\) 、単位は [S](ジーメンス)です。インピーダンスの記号は \(Z\) 、単位は [Ω](オーム)を使います。
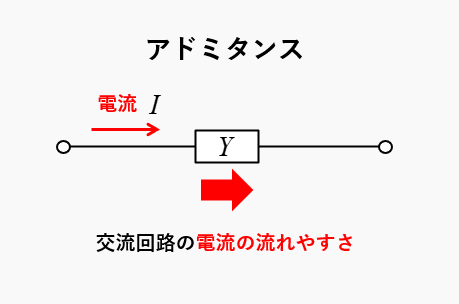
アドミタンスとインピーダンスのイメージを、図にすると次のようになります。
- アドミタンスは、交流回路の電流の流れやすさを表す言葉です。
- アドミタンスの記号 \(Y\)
- アドミタンスの単位 [S]
(読み方 ジーメンス)
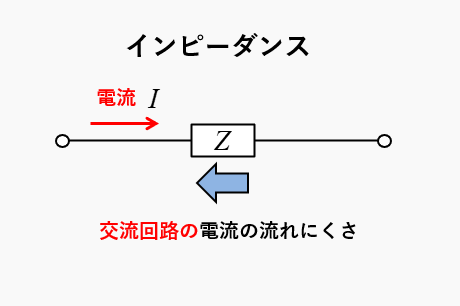
- インピーダンスは、交流回路の電流の流れにくさを表す言葉です。
- インピーダンスの記号 \(Z\)
- インピーダンスの単位 [Ω]
(読み方 オーム)
アドミタンスとインピーダンスの関係
アドミタンスとインピーダンスは、逆数の関係にありますので、次のような関係式で表すことができます。
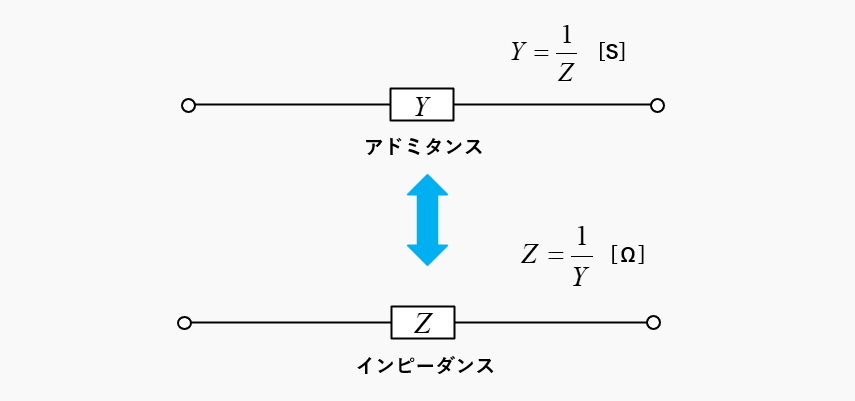
\(Y=\cfrac{1}{Z}\) [S]
\(Z=\cfrac{1}{Y}\) [Ω]
アドミタンスとオームの法則
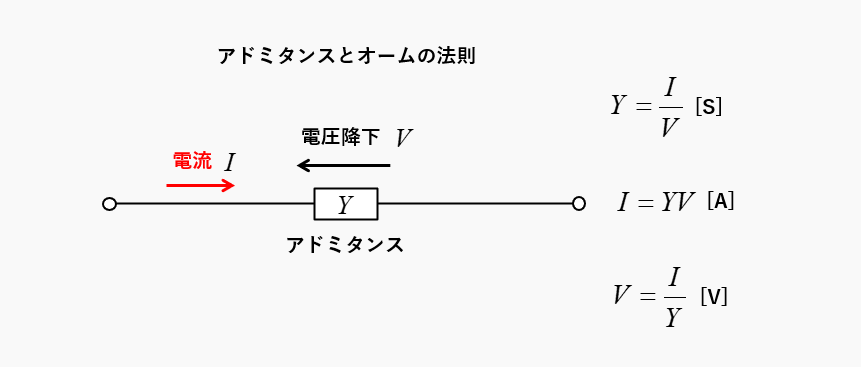
アドミタンスとオームの法則の関係は、次のようになります。
- アドミタンス・・・\(Y=\cfrac{I}{V}\) [S]
- 電流・・・\(I=YV\) [A]
- 電圧・・・\(V=\cfrac{I}{Y}\) [V]
アドミタンスを構成するもの
アドミタンスは、コンダクタンスとサセプタンスで構成される。
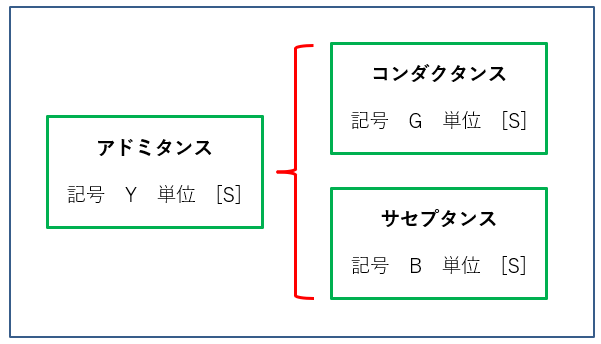
アドミタンスの表わし方
- アドミタンスは、交流回路の電流と電圧の比で、電流の流れやすさを表します。
- アドミタンスの記号 \(Y\)
- アドミタンスの単位 [S](ジーメンス)
アドミタンスを \(Y\) 、コンダクタンスを \(G\) 、サセプタンスを \(B\) とすると、アドミタンス \(Y\) は、実数部 \(G\) と虚数部 \(B\) で次の式で表します。
\(Y=G+jB\) [S]
アドミタンスの実数部をコンダクタンスといい、虚数部をサセプタンスといいます。
アドミタンスとインピーダンスの関係
抵抗・コイル・コンデンサの各素子とアドミタンス、インピーダンスの関係を式で表すと次のようになります。
| 素子 | アドミタンス | インピーダンス |
| 抵抗 | \(G=\cfrac{1}{R}\) | \(R\) |
| コイル | \(Y_L=\cfrac{1}{jωL}\) | \(Z_L=jωL\) |
| コンデンサ | \(Y_C=jωC\) | \(Z_C=\cfrac{1}{jωC}\) |
コイルによるサセプタンスを誘導性サセプタンスといい、\(Y_L\) で表示する。
コンデンサによるサセプタンスを容量性サセプタンスといい、\(Y_C\) で表示する。
\(Y=\cfrac{1}{Z}=G+jB\)\(=\cfrac{1}{R+jX}\) [S]
分母を有理化すると、次のようになります。
\(Y=G+jB\)\(=\left(\cfrac{R}{R^2+X^2}-j\cfrac{X}{R^2+X^2} \right)\)
なぜ、アドミタンスを使うのか
回路の計算にアドミタンスを使うと 計算が簡単になる場合があります。そのため、アドミタンスを使います。
例題
次の回路のインピーダンスを求めよ。
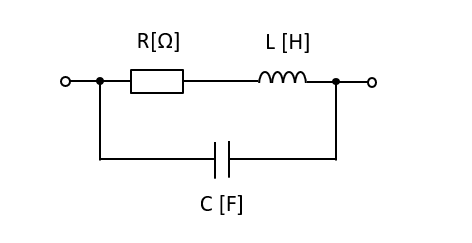
インピーダンスの計算をする場合、計算に分数が入ってくるのでどうしても複雑になりやすい。そこで、できるだけ計算式の分母や分子に、分数を含ませないようにすることが重要になります。
インピーダンスのままで計算
抵抗とコイルのインピーダンスは、\(R+jωL\) です。求めたインピーダンスとコンデンサの合成インピーダンスは、和分の積の公式が使えます。
\(Z=\cfrac{(R+jωL)\cfrac{1}{jωC}}{R+jωL+\cfrac{1}{jωC}}\)
\(Z=\cfrac{\cfrac{R+jωL}{jωC}}{\cfrac{1-ω^2LC+jωCR}{jωC}}\)
\(Z=\cfrac{R+jωL}{1-ω^2LC+jωCR}\)
この計算は途中を少し省いてありますが分母、分子に共に分数を含むため、通分が多くなりとても面倒な計算になります。
アドミタンスで計算
アドミタンスで計算すると、並列接続の場合はアドミタンスの足し算なので次のようになります。
\(Y=\cfrac{1}{R+jωL}+jωC=\cfrac{1-ω^2LC+jωCR}{R+jωL}\)
インピーダンスを求めるには、式の逆数を取れば良い。
\(Z=\cfrac{R+jωL}{1-ω^2LC+jωCR}\)
アドミタンスの計算例
次の回路に流れる合成電流 \(I_0\) を求めよ。
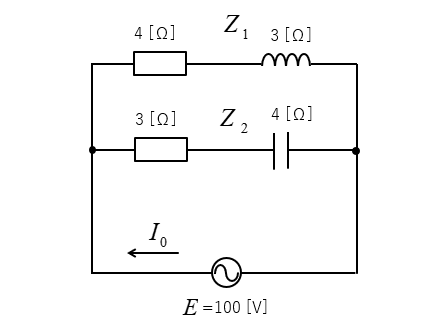
<解答例>
\(Z_1\) と \(Z_2\) をアドミタンスで求めます。
\(Y_1=\cfrac{1}{Z_1}=\cfrac{1}{4+j3}\)
\(Y_2=\cfrac{1}{Z_2}=\cfrac{1}{3-j4}\)
並列接続のアドミタンスは、足せばよいので
\(Y=Y_1+Y_2\)\(=\cfrac{1}{4+j3}+\cfrac{1}{3-j4}\)
\(Y=\cfrac{4-j3+3+j4}{25}\)\(=\cfrac{7+j}{25}\)
\(I_0=EY\)\(=100\left(\cfrac{7+j}{25}\right)=4(7+j)\)
\(I_0\) の大きさは 、次のようになります。
\(|I_0|=4\sqrt{7^2+1^2}\)
\(I_0=4\sqrt{50}=20\sqrt2\) [A]
以上で「アドミタンスとは何か」の説明を終わります。