コンダクタンスとは、電気回路における電流の流れやすさを表す言葉です。電気で最初に習う抵抗は、電流の流れにくさを表す言葉です。コンダクタンスと抵抗は、逆の関係にあります。
この記事では、コンダクタンスの記号や単位、オームの法則との関係について、また、合成コンダクタンスの求め方を説明します。
コンダクタンスとは

- 直流回路では、抵抗の逆数をいいます。
- 交流回路では、アドミタンスの実数部をいいます。
コンダクタンスの記号や単位
コンダクタンスの記号は \(G\) 、単位は [S](ジーメンス)です。抵抗の記号は \(R\) 、単位は [Ω](オーム)を使います。
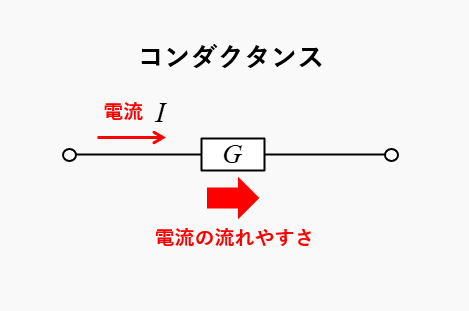
コンダクタンスと抵抗のイメージを、図にすると次のようになります。
- コンダクタンスは、電流の流れやすさを表す言葉です。
- コンダクタンスの記号 \(G\)
- コンダクタンスの単位 [S]
(読み方 ジーメンス)
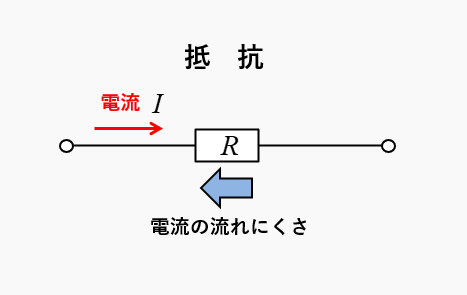
- 抵抗は、電流の流れにくさを表す言葉です。
- 抵抗の記号 \(R\)
- 抵抗の単位 [Ω]
(読み方 オーム)
コンダクタンスと抵抗の関係
コンダクタンスと抵抗は、逆数の関係にありますので、次のような関係式で表すことができます。
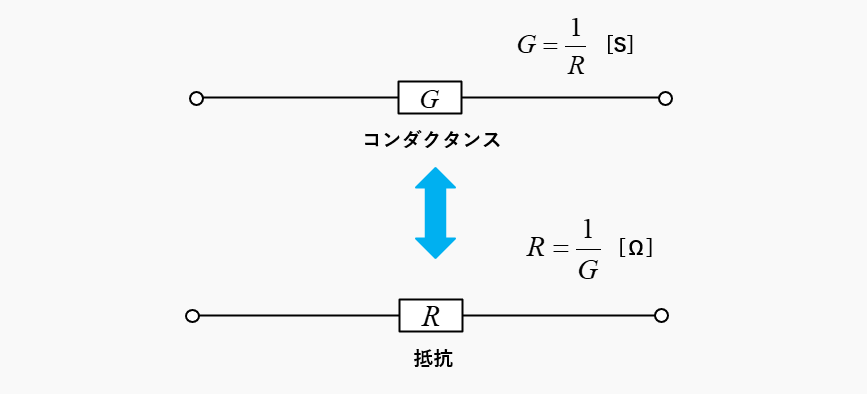
\(G=\cfrac{1}{R}\) [S]
\(R=\cfrac{1}{G}\) [Ω]
コンダクタンスとオームの法則
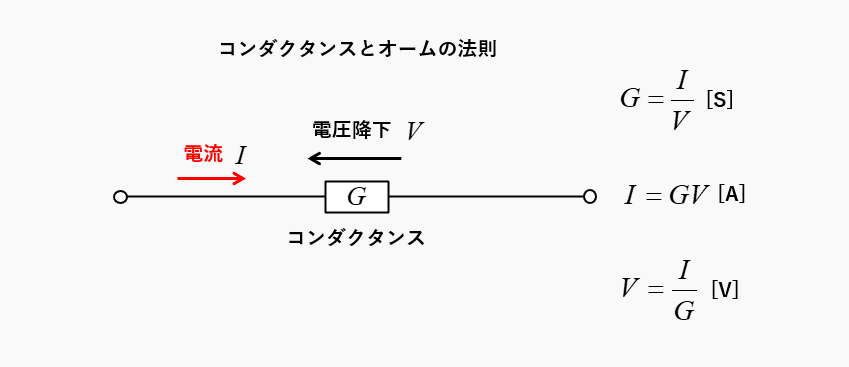
コンダクタンスとオームの法則の関係は、次のようになります。
- コンダクタンス・・・\(G=\cfrac{I}{V}\) [S]
- 電流・・・\(I=GV\) [A]
- 電圧・・・\(V=\cfrac{I}{G}\) [V]
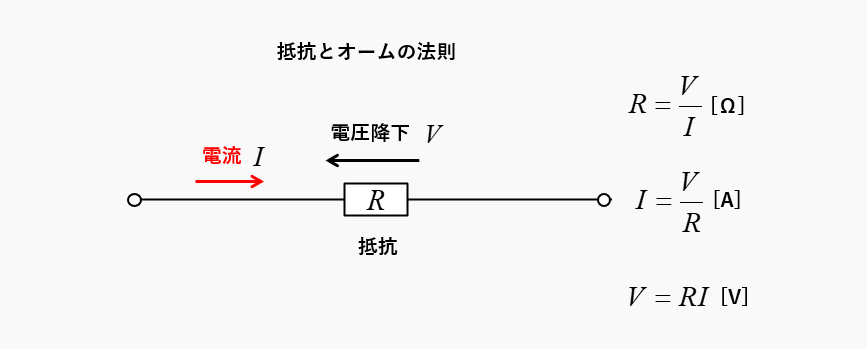
抵抗とオームの法則
抵抗とオームの法則の関係は、次のようになります。
- 抵抗・・・\(R=\cfrac{V}{I}\) [Ω]
- 電流・・・\(I=\cfrac{V}{R}\) [A]
- 電圧・・・\(V=RI\) [V]
合成コンダクタンスの求め方
複数のコンダクタンスを1つに見なしたものを合成コンダクタンスといいます。抵抗の合成抵抗を求める場合、直列接続と並列接続の計算式があります。合成コンダクタンスを求める場合も、直列接続と並列接続の計算式があります。コンダクタンスと抵抗が逆数の関係なので、直列接続と並列接続の計算式が逆になります。
並列接続のコンダクタンスの計算式
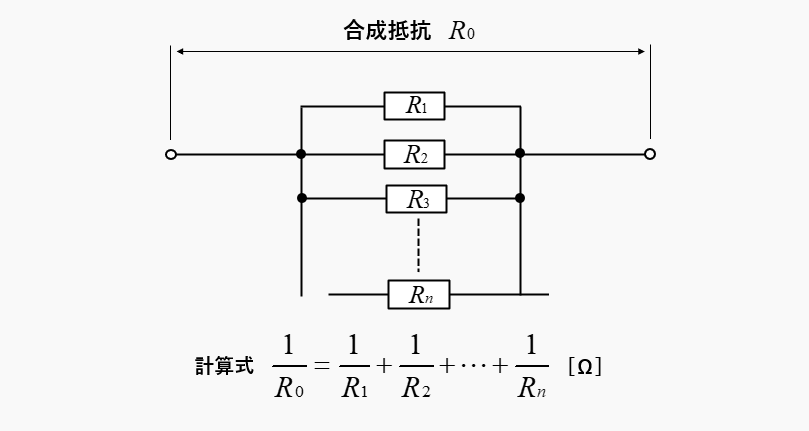
n個の抵抗が並列に接続されています。合成抵抗 \(R_0\) は
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}+\cdots+\cfrac{1}{R_n}\) です。
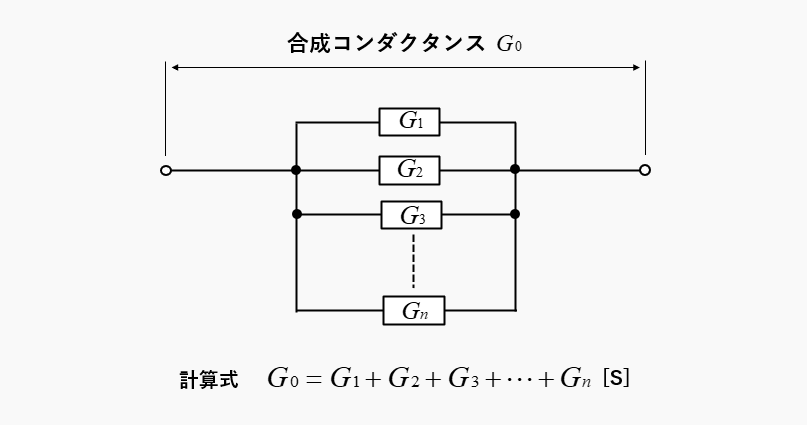
コンダクタンスは、抵抗の逆数ですから、並列接続の合成コンダクタンス \(G_0\) は
\(G_0=G_1+G_2+G_3+\cdots+G_n\) [S] で表せます。
直列接続の合成コンダクタンスの計算式
n個の抵抗が直列に接続されています。合成抵抗 \(R_0\) は
\(R_0=R_1+R_2+R_3+\cdots+R_n\) [Ω] です。

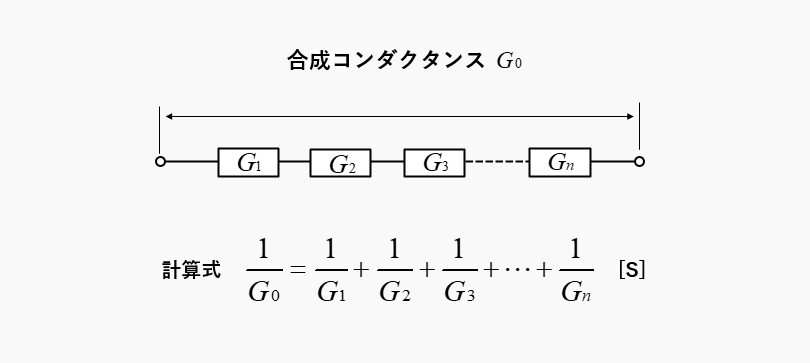
コンダクタンスは、抵抗の逆数ですから、直列接続の合成コンダクタンス \(G_0\) は
\(\cfrac{1}{G_0}=\cfrac{1}{G_1}+\cfrac{1}{G_2}+\cfrac{1}{G_3}+\cdots+\cfrac{1}{G_n}\) [S] で表せます。
直流回路のコンダクタンスは、抵抗の逆数のことです。交流回路のコンダクタンスは、アドミタンスの実数部になります。アドミタンスは、インピーダンスの逆数のことです。
■ 交流回路のコンダクタンス
交流回路のコンダクタンスは、アドミタンスの実数部 \(G\) をいいます。アドミタンス \(Y\) は、実数部 \(G\) と虚数部 \(B\) で
\(Y=G+jB\) [S] になります。

以上で「コンダクタンスについて」の説明を終わります。