供給された電力のうち、負荷で有効に使われる電力の割合を示すものが力率です。
供給された電力のすべてが、負荷で有効に使われることが理想です。しかし、交流回路では負荷の種類によって、供給された電力が有効に使われる割合が違います。
負荷設備にはコイルやコンデンサなどがあるため、遅れ電流や進み電流が流れます。電圧と電流の間にある 位相差 が、力率を変化させます。
力率は、皮相電力に対する有効電力の割合で求めます。
皮相電力と有効電力、無効電力の関係について

電圧に対し遅れ電流が流れている時の、皮相電力と有効電力、無効電力の関係は図のようになります。
| 計算式 | 単位 | |
| 皮相電力 | \(S=VI\) | [VA] ボルトアンペア |
| 有効電力 | \(P=VI\cosθ\) | [W] ワット |
| 無効電力 | \(Q=VI\sinθ\) | [var] バール |
力率の求め方
皮相電力と有効電力の関係から分かる通り、力率は有効電力を皮相電力で割ったものになります。
力率 \(\cosθ=\cfrac{P}{S}\)
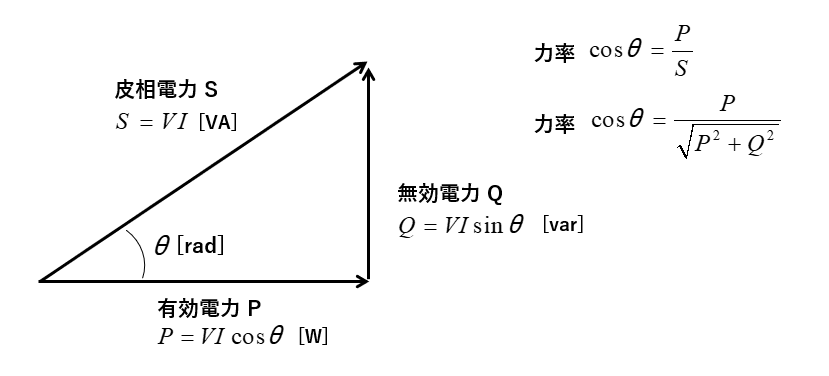
皮相電力と有効電力、無効電力の間には、三平方の定理から \(S^2=P^2+Q^2\) の関係があります。
\(S=\sqrt{P^2+Q^2}\) なので
力率 \(\cosθ=\cfrac{P}{\sqrt{P^2+Q^2}}\) から求めることもできます。
インピーダンスから求める
RLCの直列回路の力率は、インピーダンスと抵抗から求めることができます。
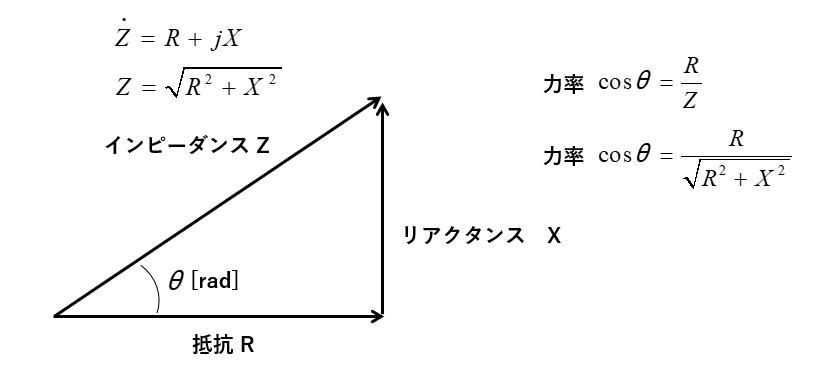
力率 \(\cosθ=\cfrac{R}{Z}\)
力率 \(\cosθ=\cfrac{R}{\sqrt{R^2+X^2}}\)
力率の求め方の例題
図のような、交流電源に \(20\) [W] の負荷を接続した時、電力計が \(25\) [W] の消費電力になりました。力率を求めよ。
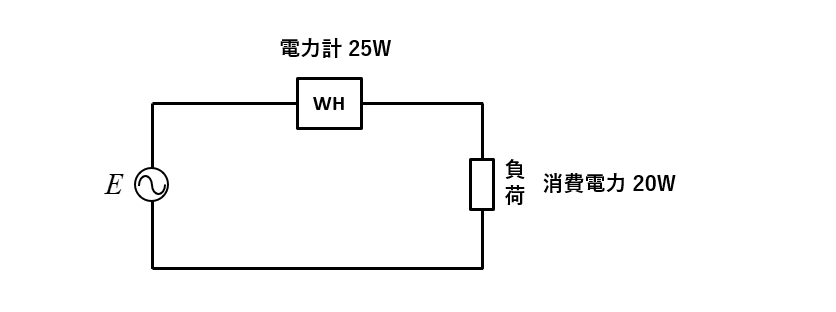
力率 \(\cosθ=\cfrac{P}{S}\)
力率のから、力率 \(\cosθ=\cfrac{P}{S}=\cfrac{20}{25}=0.8\) なので、力率は80%になります。
まとめ
電源から送られた皮相電力が負荷で、有効電力になる割合のことを 力率 といいます。
皮相電力をS、有効電力をP、無効電力をQとすると力率の公式は、次のようになります。
力率 \(\cosθ=\cfrac{P}{S}\)
\(S=\sqrt{P^2+Q^2}\) なので
力率 \(\cosθ=\cfrac{P}{\sqrt{P^2+Q^2}}\) から求めることもできます。
以上で「力率とは何か?力率の求め方をやさしく解説!」を終わります。