- 交流回路のリアクタンスとは何か?
- リアクタンスの種類
- リアクタンスの記号と単位
について説明します。
交流回路の リアクタンス とは、コイル(インダクタンス)や コンデンサ(キャパシタンス)における 電圧と電流の比 をいいます。
抵抗が直流回路における 電圧と電流の比 で表したのと似ています。
リアクタンスの単位は 抵抗と同じように オーム [Ω] で表します。
リアクタンスは 誘導性リアクタンスと容量性リアクタンス の2種類あります。
ここでは、リアクタンスについての説明をします。
誘導性リアクタンス
誘導性リアクタンス とは コイルのインダクタンスが交流回路の 電流の流れを妨げる働き をするものです。
コイルの回路に、交流電圧を加えた場合の回路図です。

誘導性リアクタンスの表し方
\(L\) はコイルの インダクタンス で単位は ヘンリー [H] を使います。
誘導性リアクタンス は \(X_L\) で表し、単位は抵抗と同じく オーム [Ω] を使います。
式にすると次のようになります。
\(X_L=\cfrac{E}{I}\) [Ω]
電流の式にすると次のようになります。
\(I=\cfrac{E}{X_L}\) [A]
誘導性リアクタンスは周波数に比例する
誘導性リアクタンス \(X_L\) は、電源の周波数を \(f\) [Hz] コイルのインダクタンスを \(L\) [H] とすると、次の式になります。
\(X_L=2πfL\) [Ω]
■ 誘導性リアクタンスの大きさは周波数に 比例 します。
つまり、周波数が高くなると、誘導性リアクタンスは大きくなり、そのため回路の電流は小さくなります。
\(I=\cfrac{E}{X_L}=\cfrac{E}{2πfL}\) [A]
また \(2πf=ω\) として
\(X_L=ωL\) [Ω]
虚数単位 \(j\) を使うと
\(jX_L=jωL\) [Ω] とすることもあります。
容量性リアクタンスとは
容量性リアクタンス はコンデンサの静電容量(キャパシタンス)が交流回路において 電流の流れを妨げる働き をするものです。
コンデンサの回路に交流電圧を加えた場合の回路図です。
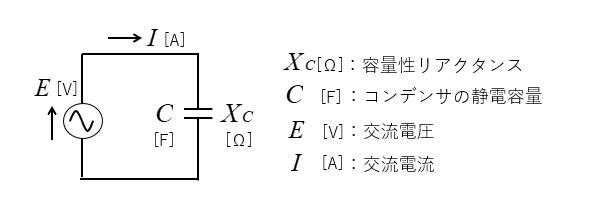
容量性リアクタンスの表し方
\(C\) はコンデンサの キャパシタンス で 単位は ファラド [F] を使います。
容量性リアクタンス は \(X_C\) で表し、単位は抵抗と同じく オーム [Ω] を使います。
式にすると次のようになります。
\(X_C=\cfrac{E}{I}\) [Ω]
電流の式にすると次のようになります。
\(I=\cfrac{E}{X_C}\) [A]
容量製リアクタンスは周波数に反比例する
容量性リアクタンス \(X_C\) は、電源の周波数を \(f\) [Hz] コンデンサのキャパシタンスを \(C\) [F] とすると、次のようになります。
\(X_C=\cfrac{1}{2πfC}\) [Ω]
■ 容量性リアクタンスの大きさは周波数に 反比例 します。
つまり、周波数が高くなると、容量性リアクタンスは小さくなり、そのため回路の電流は大きくなります。
誘導性リアクタンスと 逆の働き というわけです。
\(I=\cfrac{E}{X_C}\)\(=\cfrac{E}{\cfrac{1}{2πfC}}\)\(=2πfCE\) [A]
また \(2πf=ω\) として
\(X_C=\cfrac{1}{ωC}\) [Ω]
虚数単位 \(j\) を使うと
\(-jX_C=-j\cfrac{1}{ωC}\)\(=\cfrac{1}{jωC}\) [Ω] とすることもあります。
■ 虚数単位 \(j\) を付ける場所
- 虚数単位がややこしくなるのは、どこに付けたらいいかわからない。
- \(+j、-j\) どっちになるかわからない。ということではないでしょうか
■ 虚数単位 \(j\) は、\(ω\)(オメガ)の前に \(+j\) を付けると覚えましょう。
これを覚えれば、かなりの部分が解決すると思います。
- \(+j\) は反時計方向に90°移動します。
- \(-j\) は時計方向に90°移動します。
リアクタンスのまとめ
誘導性リアクタンス
\(X_L=ωL\) [Ω]
容量性リアクタンス
\(X_C=\cfrac{1}{ωC}\) [Ω]
■ インピーダンス \(Z\) は、抵抗 \(R\) とリアクタンス \(X\) を合成したものです。
リアクタンス \(X\) は インピーダンス \(Z\) から抵抗 \(R\) を取り除いたものになります。
誘導性リアクタンスを \(X_L\) 容量性リアクタンスを \(X_C\) とすると
リアクタンス \(X\) は
\(X=X_L-X_C\) [Ω] になります。
練習問題
問題1
\(132.7\) [mH] のインダクタンスがあります。
周波数 60Hz、600Hz、6000Hz のときの正弦波の対する、リアクタンスを求めよ。
<解答例>
■ 周波数 60Hz のとき
インダクタンスのリアクタンス \(X_L\) は
\(X_L=ωL=2πfL\)\(=2π×60×132.7×10^{-3}\)\(=50\) [Ω]
■ 周波数 600Hz のとき
インダクタンスのリアクタンス \(X_L\) は
\(X_L=ωL=2πfL\)\(=2π×600×132.7×10^{-3}\)\(=500\) [Ω]
■ 周波数 6000Hz のとき
インダクタンスのリアクタンス \(X_L\) は
\(X_L=ωL=2πfL\)\(=2π×6000×132.7×10^{-3}\)\(=5000\) [Ω] になります。
問題2
\(50\) [Hz] において、\(318.3\) [mH] の インダクタンスと同じ大きさのリアクタンスを持つ、静電容量を求めよ。
<解答例>
インダクタンスのリアクタンス \(X_L\) を求めると
\(X_L=ωL=2πfL\)\(=2π×50×318.3×10^{-3}\)\(=31.8π\) [Ω]
インダクタンスのリアクタンスと、同じ大きさの静電容量のリアクタンス \(X_C\) を求めると
\(X_C=\cfrac{1}{ωC}=X_L\) なので
\(\cfrac{1}{ωC}\)\(=\cfrac{1}{2π×50×C}=31.8π\)
\(C=\cfrac{1}{2π×50×31.8π}\)\(=31.8×10^{-6}\) [F] から
\(C=31.8\) [μF] の静電容量となります。
以上で「リアクタンスとは何か?」の説明を終わります。
