交流回路のインピーダンス計算式のまとめ

直列接続と並列接続のインピーダンス計算式のまとめ。

RL直列回路の計算式

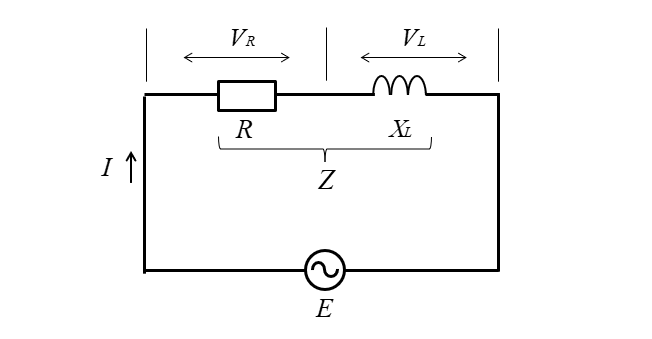
RL直列回路
インピーダンス	\(\dot{Z}=R+jX_L\)
	\(Z=\sqrt{R^2+{X_L}^2}\)
各素子の電圧	\(V_R=RI\)
	\(V_L=X_LI\)
電流	\(I=\cfrac{E}{Z}\)

RC直列回路の計算式

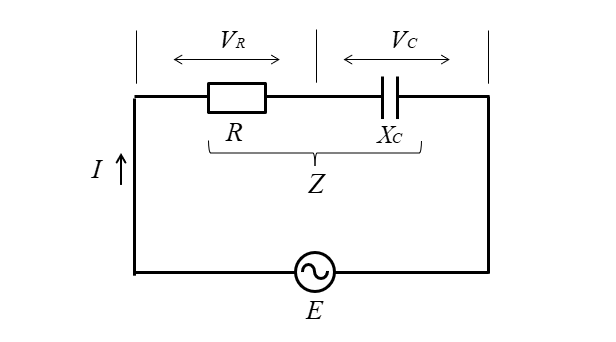
RC直列回路
インピーダンス	\(\dot{Z}=R-jX_C\)
	\(Z=\sqrt{R^2+{X_C}^2}\)
各素子の電圧	\(V_R=RI\)
	\(V_C=X_CI\)
電流	\(I=\cfrac{E}{Z}\)

RL並列回路の計算式

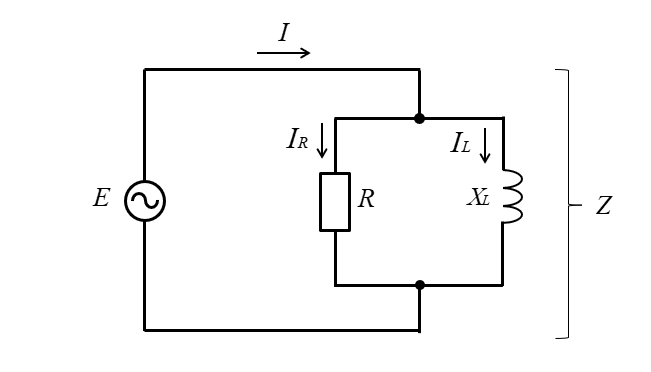
RL並列回路
インピーダンス	\(\cfrac{1}{\dot{Z}}=\cfrac{1}{R}+\cfrac{1}{jX_L}\)
	\(Z=\cfrac{RX_L}{\sqrt{R^2+{X_L}^2}}\)
各素子の電流	\(I_R=\cfrac{E}{R}\)
	\(I_L=\cfrac{E}{X_L}\)
電流	\(I=\sqrt{{I_R}^2+{I_L}^2}\)

RC並列回路の計算式

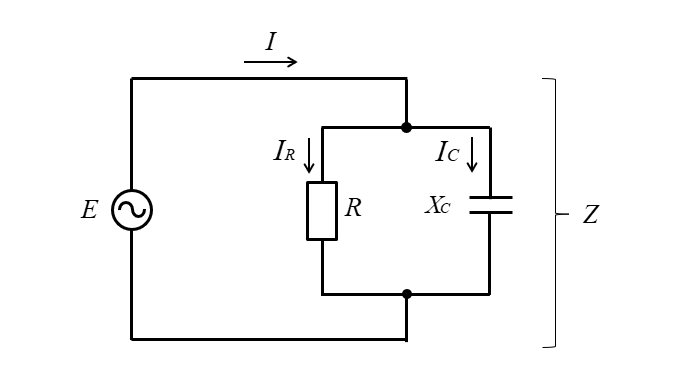
RC並列回路
インピーダンス	\(\cfrac{1}{\dot{Z}}=\cfrac{1}{R}+\cfrac{1}{-jX_C}\)
	\(Z=\cfrac{RX_C}{\sqrt{R^2+{X_C}^2}}\)
各素子の電流	\(I_R=\cfrac{E}{R}\)
	\(I_C=\cfrac{E}{X_C}\)
電流	\(I=\sqrt{{I_R}^2+{I_C}^2}\)

RLC直列回路の計算式

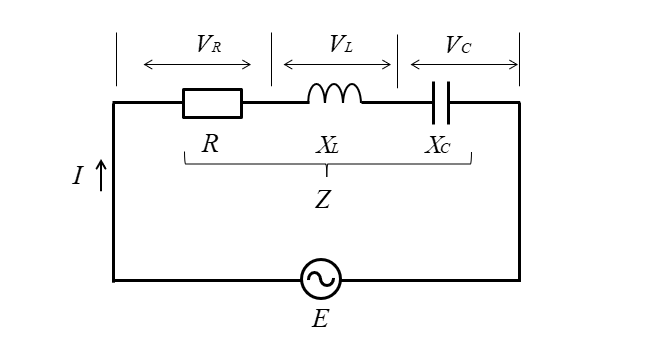
RL直列回路
インピーダンス	\(\dot{Z}=R+j(X_L-X_C)\)
	\(Z=\sqrt{R^2+{(X_L-X_C)}^2}\)
各素子の電圧	\(V_R=RI\)
	\(V_L=X_LI\)
	\(V_C=X_CI\)
電流	\(I=\cfrac{E}{Z}\)

RLC並列回路の計算式

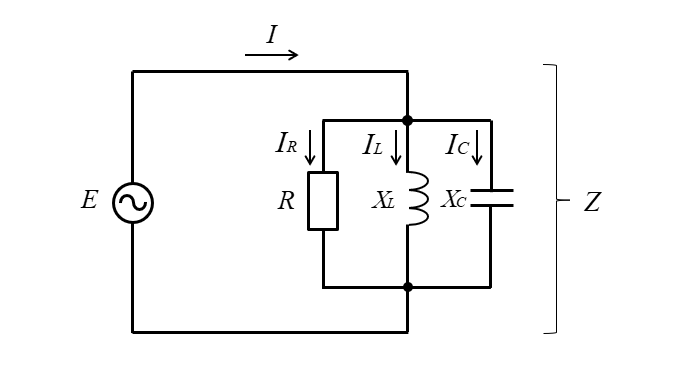
RLC並列回路
インピーダンス	\(\cfrac{1}{\dot{Z}}=\cfrac{1}{R}+\cfrac{1}{j}(\cfrac{1}{X_L}-\cfrac{1}{X_C})\)
	\(\cfrac{1}{X}=\cfrac{1}{X_L}-\cfrac{1}{X_C}\)　とすると \(Z=\cfrac{RX}{\sqrt{R^2+{X}^2}}\)
各素子の電流	\(I_R=\cfrac{E}{R}\)
	\(I_L=\cfrac{E}{X_L}\)
	\(I_C=\cfrac{E}{X_C}\)
電流	\(I=\sqrt{{I_R}^2+(I_L-I_C)^2}\)

以上で「交流回路のインピーダンス計算式のまとめ」の説明を終わります。