- ベクトルの記号と表記の仕方
- ベクトル図の書き方
- 交流回路のベクトルの書き方
について説明しています。
ベクトルとは
ベクトルとは「大きさ」と「向き」を持つ量のことです。
量を表すには「ベクトル量」と「スカラー量」があります。
■ ベクトル量=大きさと方向を持つ量
速度、加速度、力、運動量、角運動量、電流などがあります。
■ スカラー量=大きさのみの量
長さ、質量、時間、温度、電荷、エネルギーなど
ここではベクトルの書き方の基本的なことについて説明します。
ベクトルの書き方の基本
■ ベクトルの文字の表記方法はドットを付ける。
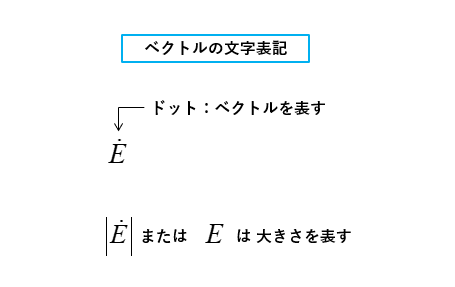
■ ベクトルの図形の表記方法

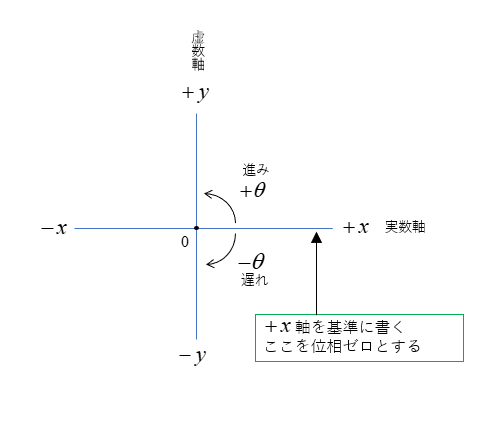
ベクトル図の説明
- x軸を実数軸、y軸を虚数軸といいます。
- +x軸の位置を位相ゼロとして、ベクトルを書きます。
- 反時計方向は位相の進み方向になります。時計方向は位相の遅れ方向になります。
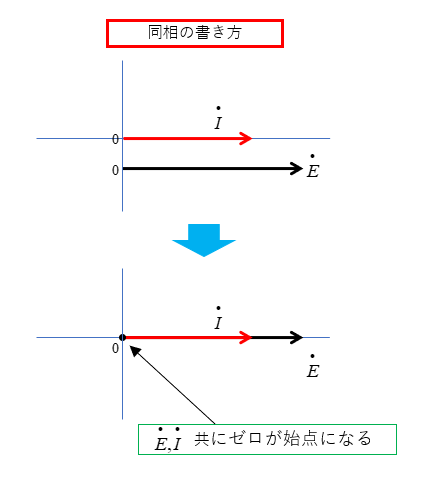
■ 位相が同相のときの表示
ベクトル(電圧と電流)が、同相のときは
始点(ゼロ)を基準に描きます。
同相のベクトルは、1本のベクトルで表示します。
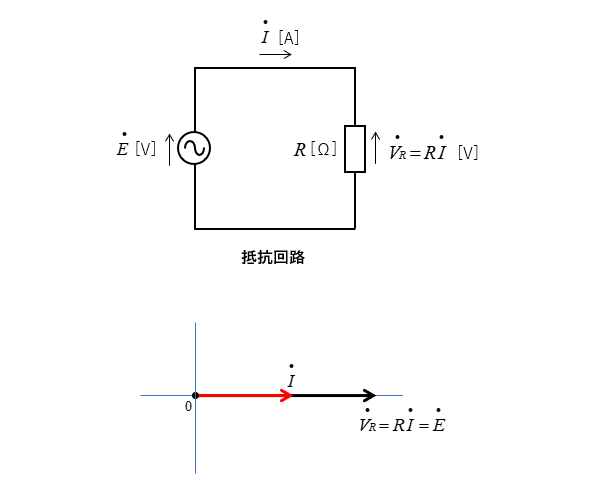
抵抗回路のベクトル図
抵抗回路のベクトルは、電源電圧、電流、抵抗の電圧降下が同相になるので
基準ベクトルに何をとっても同じになります。
抵抗に流れる 電流 と抵抗にかかる 電圧 の位相は同じになリます。
コイル回路のベクトル図
コイル回路のベクトルは
コイルに流れる電流と電圧の間に
\(\cfrac{π}{2}\) [rad](90度)の位相差があります。

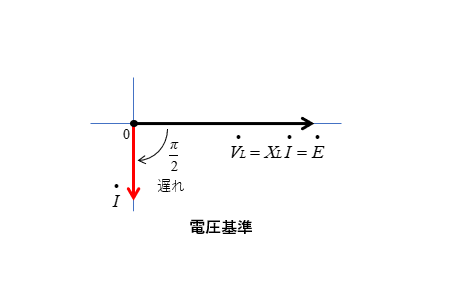
■ 電圧を基準
コイルに掛かる「電圧を基準」にすると
電流は \(\cfrac{π}{2}\) [rad] 遅れます。
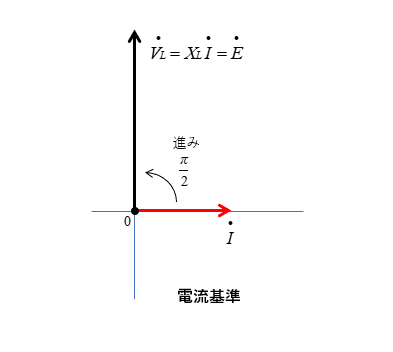
■ 電流を基準
電圧は \(\cfrac{π}{2}\) [rad] 進みます。
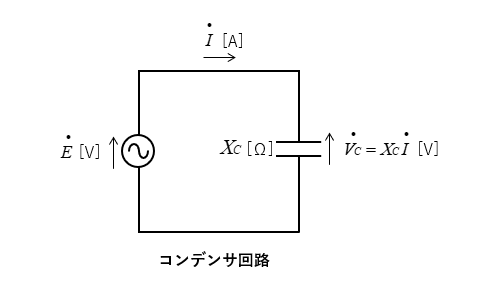
コンデンサ回路のベクトル図
コンデンサ回路のベクトルは
コンデンサに流れる電流と電圧の間に
\(\cfrac{π}{2}\) [rad](90度)の位相差があります。
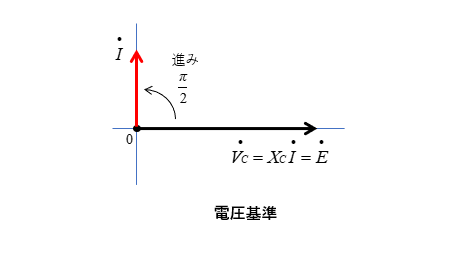
■ 電圧を基準
コンデンサに掛かる「電圧を基準」にすると
電流は \(\cfrac{π}{2}\) [rad] 進みます。
■ 電流を基準
コンデンサに流れる「電流を基準」にすると
電圧は \(\cfrac{π}{2}\) [rad] 遅れます。
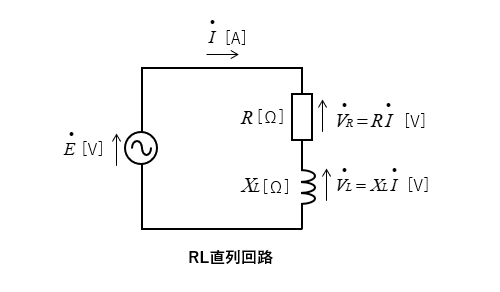
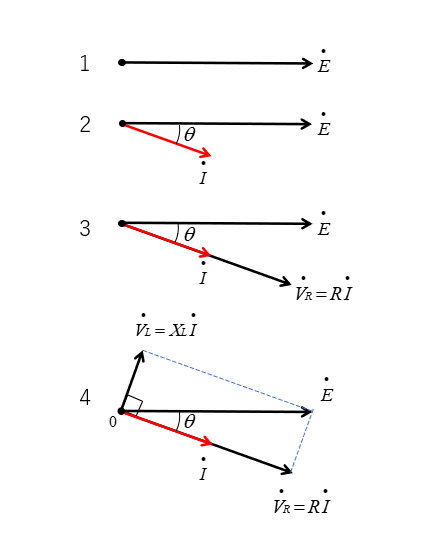
RL直列回路のベクトルの書き方
- 直列回路では回路の素子に流れる電流が同じになります。
- 電流を基準ベクトルとして、それぞれの素子に掛かる電圧をベクトル表示します。
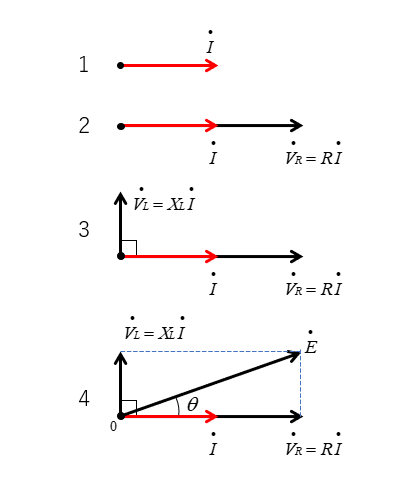
電流を基準に書く

RL直列回路は、回路に流れる電流が同じになります。
- 電流を基準ベクトルとして、x軸に書きます。
- 抵抗の電圧降下は電流と同相になりますので、電流と同相で書きます。
- コイルの電圧は、コイルに流れる電流より \(\cfrac{π}{2}\) [rad] 進みます。時計方向に書きます。
- 抵抗の電圧降下とコイルの電圧のベクトル和が、電源電圧になります。
電圧を基準に書く方法
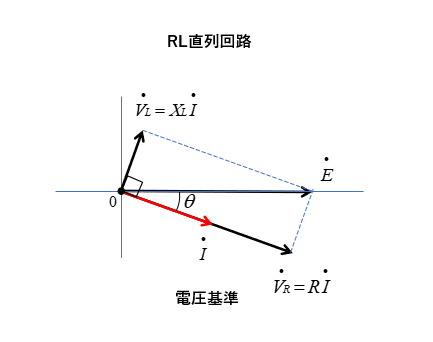
- 電源電圧を基準ベクトルとして、x軸に書きます。
- RL直列回路なので、電流は電源電圧に対して遅れ電流になります。遅れ電流として書きます。
- 抵抗の電圧降下は電流と同相になるので、電流と同相に書きます。
- コイルに掛かる電圧は、電流より \(\cfrac{π}{2}\) [rad] 進みます。
- 抵抗の電圧降下とコイルの電圧のベクトル和が、電源電圧になります。
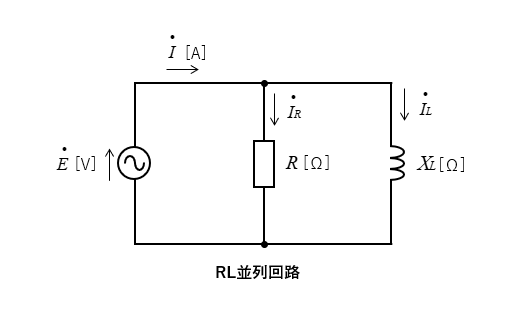
RL並列回路のベクトルの書き方
- 並列回路では回路の素子に掛かる電圧が同じになります。
- 電圧を基準ベクトルとして、それぞれの素子に流れる電流をベクトル表示します。
電圧を基準に書く
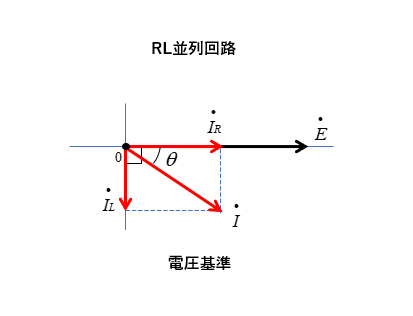
- 電源電圧を基準ベクトルとして、x軸に書きます。
- RL並列回路なので、抵抗に流れる電流は電源電圧と同相になります。
- コイルに流れる電流は、コイルに掛かる電圧より \(\cfrac{π}{2}\) [rad] 遅れます。
- 抵抗に流れる電流とコイルに流れる電流のベクトル和が、回路全体に流れる電流になります。
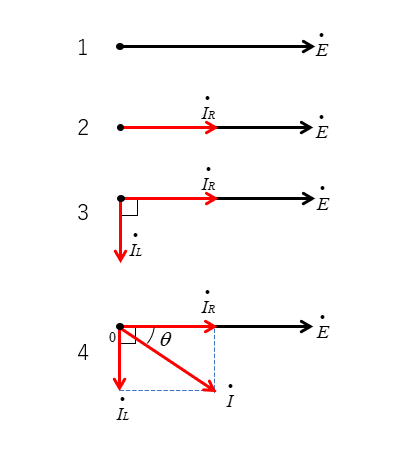
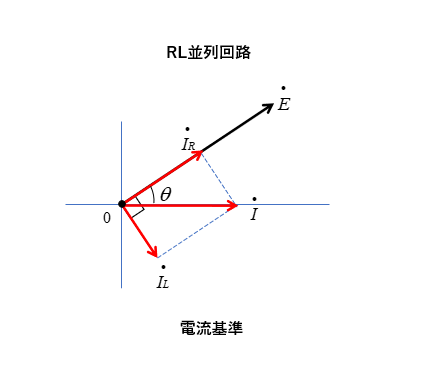
電流を基準に書く
ベクトルの合成
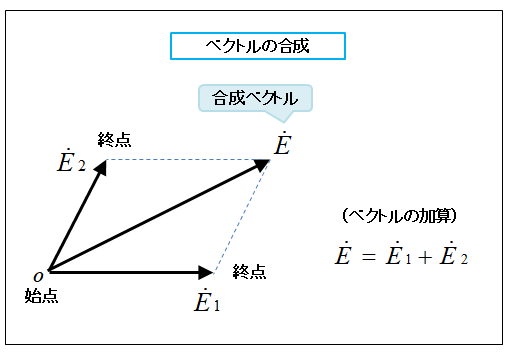
■ ベクトルを加算するには、ベクトル \(E_1\) と \(E_2\) の始点を合わせます。
- ベクトル \(E_1\) の終点から \(E_2\) の平行線を引く。
- 同じく、ベクトル \(E_2\) の終点から \(E_1\) の平行線を引く。
- この両線の交点に、始点から矢印を引きます。
- この矢印の線が、ベクトル \(E_1\) と \(E_2\) を加算したベクトル E になります。
ベクトルの求め方
ベクトルの考え方を力で考えてみましょう。
図1のように 2 [N] のちからが同じ方向に働いている時は
単純に2つを合わせれば良いので 4 [N] ニュートンになります。

ベクトルの加法
ベクトルを求めるには図2のように
2つの力で平行四辺形を作り合成することができます。
平行四辺形の対角線にあたるところが合成された力になります。

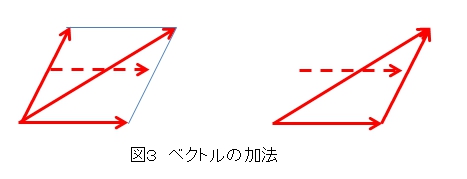
また、図3のように1つの辺を平行移動させて作る方法もあります。
以上で「ベクトルの書き方の基本」の説明を終わります。