直交座標表示と極座標表示について

直交座標表示と極座標表示

ある場所の位置を示す方法として

直交座標表示と極座標表示というものがあります。

電気回路の交流を表すときに、よく利用しますので覚えておくと便利です。

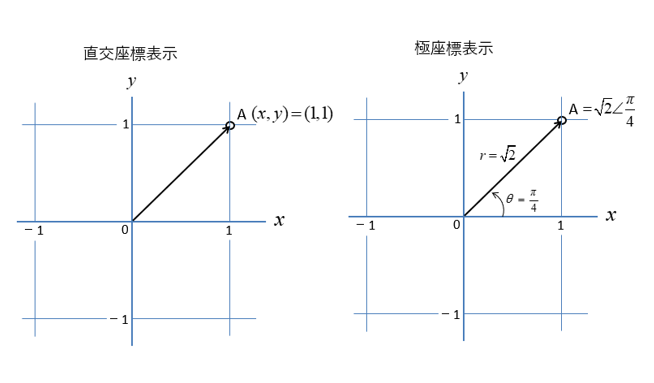
直交座標表示

点 A の座標を　\((x,y)\)　のように表示する方法を

直交座標表示といいます。

A点の座標は　\(x=1,y=1\)　なので

\(A(x,y)=(1,1)\)　で表されます。

極座標表示

A点の座標を長さと角度で表す方法を

極座標表示といいます。

中心からの距離を　\(r\)、\(x\)　軸からの角度を　\(θ\)　とすると

A点の座標は、\(A(r,θ)\)　となります。

A点の座標を極座標表示すると

\(A=\sqrt2\angle \cfrac{π}{4}\)　になります。

直交座標と極座標の関係

それぞれの関係は次のようになります。

\((r,θ)→(x,y)\)　に変換

\(x=r\cosθ\)

\(y=r\sinθ\)

\((x,y)→(r,θ)\)に変換

\(r=\sqrt{x^2+y^2}\)

\(tanθ=\cfrac{y}{x}\)

以上で「直交座標表示と極座標表示について」の説明を終わります。