- 交流回路では単純に足し算ができないわけ
- 抵抗とコイルの回路の例
について説明しています。
直流回路と交流回路の違い
交流回路の計算をするときは
直流回路のように、単純に数値を「足したり、引いたり」して計算することができません。
交流回路の電圧や電流は時間の経過とともに、大きさと方向が変わります。
更に電圧でも大きさだけでなく、位相がずれている場合がありますので計算が複雑になります。
交流回路で計算するときは、ベクトルを使うと比較的簡単に計算することができます。
ここでは、交流回路の電圧や電流の計算が、単純な足し算や引き算でできないわけを説明します。
交流回路の電圧が足し算できないわけ
図のような、抵抗とコイルの直列接続された交流回路があります。
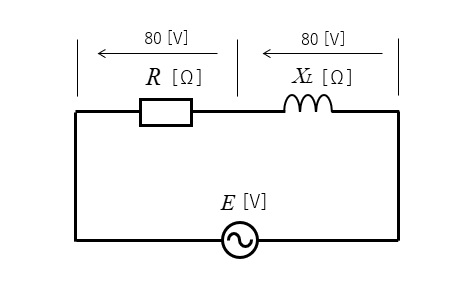
抵抗とコイルの端子電圧は、共に \(80\) [V] です。
交流回路のことを知らなければ、電源電圧 \(E\) は
\(E=80+80=160\) [V] と考えるかもしれません。
正しい電圧値は 約\(113\) [V] になります。
抵抗とコイルの電圧の関係
抵抗とコイルの直列回路の電圧や電流の図になります。
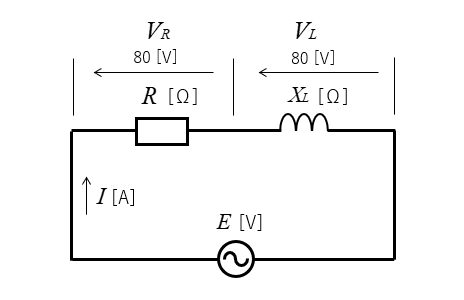
\(V_R=80\) [V] は抵抗の端子電圧
\(V_L=80\) [V] はコイルの端子電圧
\(E\) は電源電圧
\(I\) は回路に流れる電流です。
\(V_R\)、\(V_L\)、\(E\)、\(I\) は 実効値 とします。
抵抗とコイルにかかる電圧の波形について

抵抗とコイルにかかる電圧の交流波形を、描いてみると図のようになります。
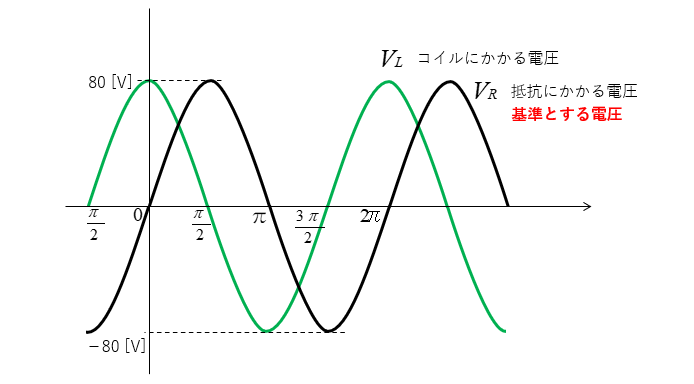
抵抗にかかる電圧 \(V_R\) を基準の波形として考えます。
ここには表示してありませんが
電流 \(I\) の波形は \(V_R\) と同じ 位相 になります。
ただし、大きさ(振幅)は異なります。
抵抗とコイルにかかる電圧の波形を合成する
抵抗とコイルにかかる電圧の波形を合成すると、次のような波形になります。
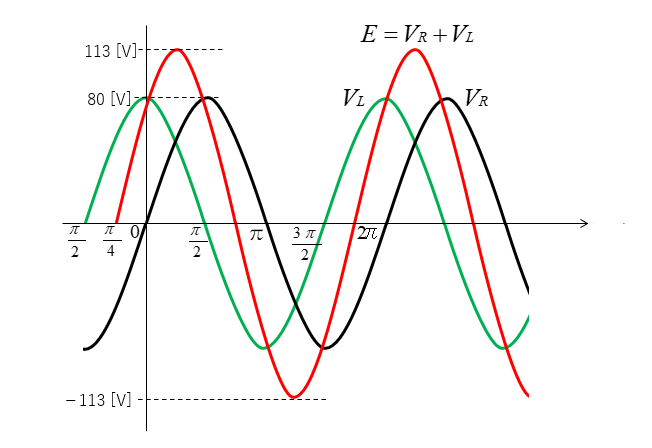
抵抗とコイルにかかる電圧の間には 位相差 があり 大きさも常に変化しているので、単純に足し算をすることができません。
抵抗だけの回路の場合
ここで、次のような抵抗だけの回路の場合を考えてみます。
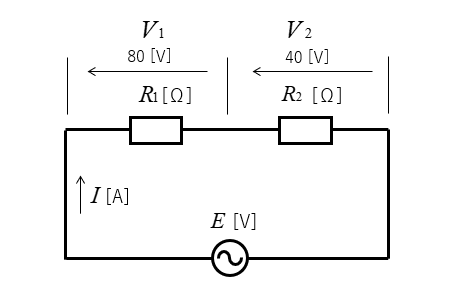
\(V_1=80\) [V] は抵抗\(R_1\) の端子電圧
\(V_1=40\) [V] は抵抗\(R_2\) の端子電圧とすると波形は次のようになります。
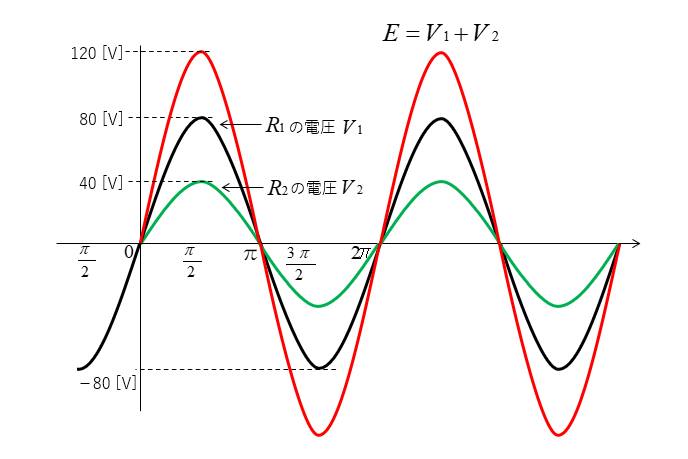
図のように、抵抗だけの回路の場合は位相が同じなので大きさを足し算することができます。
交流回路の計算にはベクトルを使うと便利
波形を見ることで位相が違うと単純に計算できないことはわかります。
しかし、交流回路の計算をするのにいちいち次のような波形を描くことはできません。

交流回路では ベクトル を描くことで、大きさと位相を知ることができます。

上の例をベクトルで表示してみましょう。
■ 基準ベクトルとして電流 \(I\) を描きます。

■ 抵抗にかかる電圧 \(V_R\) を描きます。
\(V_R\) の長さは始点からの長さです。

■ コイルにかかる電圧 \(V_L\) の位相を90度進めて描きます。
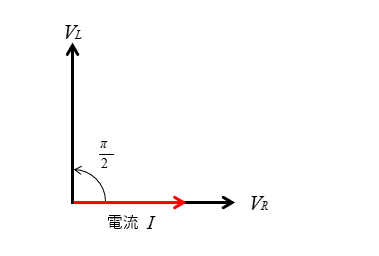
■ ベクトルを合成すると電源電圧 \(E\) になります。
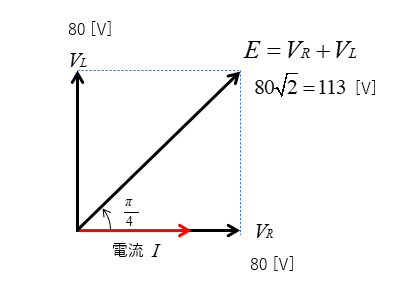
まとめ
交流回路の電圧が足し算できないわけ
交流回路では、位相が異なる場合があるので、単純に足し算で計算することができないわけです。
以上で「交流回路の電圧が足し算できないわけ」の説明を終わります。