- 虚数とは何か?
- 複素数と共役複素数
- 複素数の四則演算
について説明しています。
複素数
電気回路の計算などで
位相を含めた数式を表す場合
複素数を用いる方法を「記号法」といいます。
電気工学では電圧に対する誘導性リアクタンスの電流は90度の遅れになりますが
\(-j\) をかければ座標を表せます。
また、容量性リアクタンスの場合は電圧に対して電流は90度の進みになりますが
\(+j\) をかければ座標を表せます。
虚数とは何か
虚数とは、2乗して -1になる
想像上 (imaginary) の数で数学では \(i\) を使います。
\(i=\sqrt-1\)
両辺を2乗すると
\(i^2=-1\)
\(j=\sqrt-1\)
両辺を2乗すると
\(j^2=-1\)
\(j\) は2乗すると -1 となる数です。
つまり、\(j×j=-1\) になります。
この虚数 \(j\) を掛けるということは何を意味するかというと
複素平面において 元の位置を反時計回りに90度回転させること を意味します。
虚数があると便利なこと
- 幾何学的なベクトルの計算を複素数を使うと数式計算によって求めることができること。
- 平面の座標を表すことができる。
- まず、正の数と負の数が使える世界を考えると、右へ+3 とか 左へ-2 などのように右と左の方向を表現できます。
複素数について
複素数と共役複素数
実数と虚数 を使って、次のように表現した式を
複素数 といいます。
\(a+jb\)
\(a\) を実部といい、\(jb\) を虚部といいます。
また、虚部の符号を変えたもの \(a-jb\) を共役(きょうやく)複素数といいます。
複素平面(ガウス平面)
複素数を直交座標で表す方法を「複素数表示」といい
複素数表示の平面を「複素平面」、「ガウス平面」といいます。
■ 複素平面の表示例
\(\dot{Z}=a+jb\) を複素平面にグラフ化すると次のような図になります。
\(\dot{Z}\) の絶対値は三平方の定理から
\(Z=\sqrt{a^2+b^2}\)
また、実軸(\(x\))との角度 \(θ\) は
\(θ=tan^{-1}\cfrac{b}{a}\)
となります。
複素数に「j」や「-j」をかけるとどうなるか
複素数 \(\dot{Z}=a+jb\) に「\(j\)」や「\(-j\)」をかけてみます。
■ \(\dot{Z}=a+jb\) に「\(j\)」をかける
\(j\dot{Z}=j(a+jb)=ja+j^2b=ja-b=-b+ja\) となります。
実数だった \(a\) は虚数に、また虚数だった \(b\) は実数になりました。
■ \(\dot{Z}=a+jb\) に「\(-j\)」をかける
\(-j\dot{Z}=-j(a+jb)=-ja+b=b-ja\) となります。
実数だった \(a\) は虚数に、また虚数だった \(b\) は実数になりました。
虚数をかける
- 「\(j\)」をかけると、反時計方向に \(\cfrac{π}{2}\)(90度)移動します。
- 「\(-j\)」をかけると、時計方向に \(\cfrac{π}{2}\)(90度)移動します。
複素数の四則演算
複素数 \(a+jb\) と 複素数 \(c+jd\) の例
■ たし算
\((a+jb)+(c+jd)=(a+c)+j(b+d)\)
■ ひき算
\((a+jb)-(c+jd)=(a-c)+j(b-d)\)
■ かけ算
\((a+jb)(c+jd)=(ac-bd)+j(bc+ad)\)
■ わり算
\(\cfrac{(a+jb)}{(c+jd)}\)
\(=\cfrac{(a+jb)(c-jd)}{(c+jd)(c-jd)}\)
\(=\cfrac{ac+bd}{c^2+d^2}+j\cfrac{bc-ad}{c^2+d^2}\)
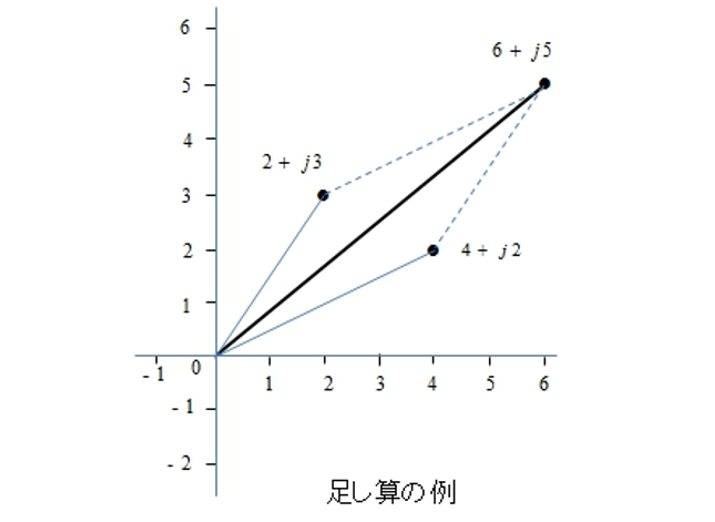
複素数のたし算
\((4+j2)+(2+j3)=6+j5\) をグラフで表示します。
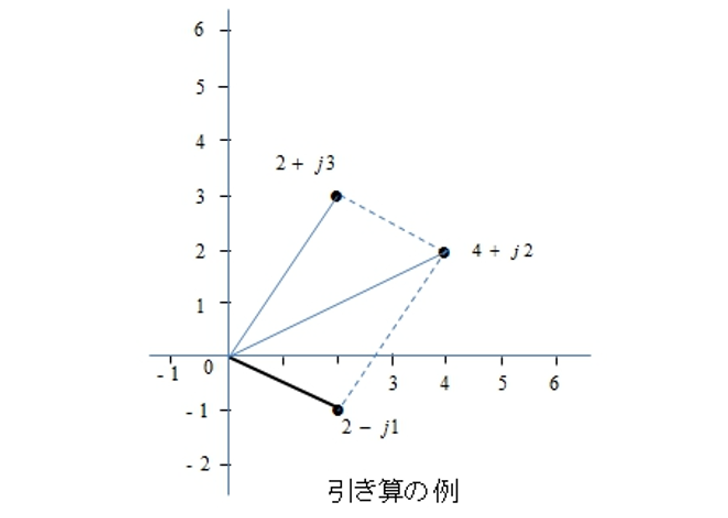
複素数のひき算
\((4+j2)-(2+j3)=2+j\) をグラフで表示します。
複素数のかけ算
\((4+j3)(5-j2)=26+j7\) をグラフで表示します。
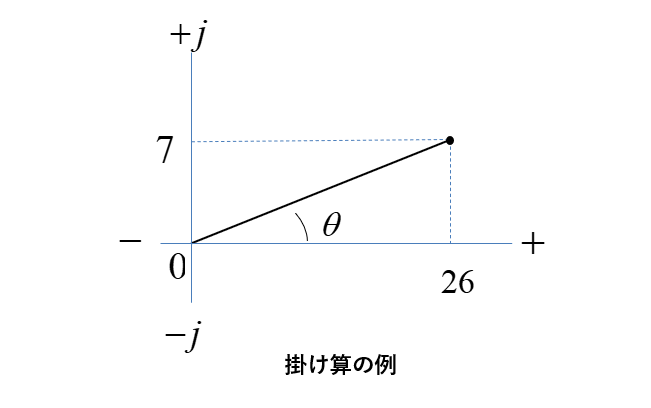
絶対値 \(\sqrt{26^2+7^2}\)
角度 \(θ=tan^{-1}\cfrac{7}{26}\)
複素数のわり算
実際の計算では、分母を実数にするための工夫をして計算していきます。
複素数の有理化をすると計算がやりやすくなります。
\(\cfrac{7-j5}{8+j6}=\cfrac{(7-j5)(8-j6)}{(8+j6)(8-j6)}\)
\(=\cfrac{26}{100}-j\cfrac{82}{100}=0.26-j0.82\) をグラフで表示します。
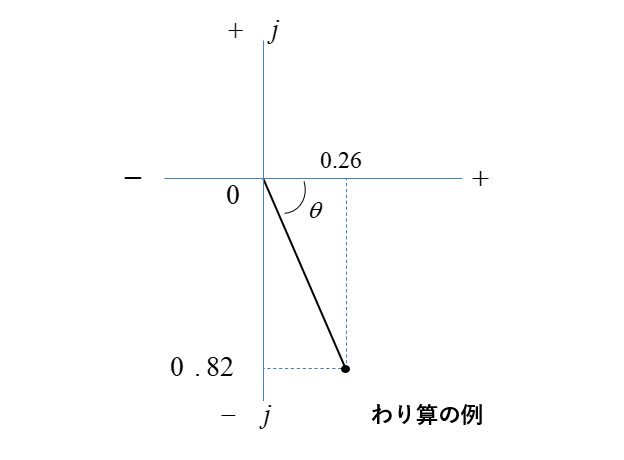
絶対値 \(\cfrac{\sqrt7400}{100}\)
角度 \(θ=tan^{-1}\cfrac{82}{26}\)
複素数の有理化
複素数の有理化とは、\(\cfrac{1}{a+jb}\) といった形の複素数を
\(c+jd\) といった形にすることです。
分母から虚数をなくして、実数部と虚数部に変換することです。
\( c+jd\) という形にするためには
\(\cfrac{1}{a+jb}\) の分母、分子のそれぞれに
\( a-jb\) を掛けてやります。
たとえば
\(\cfrac{1}{a+jb}\)
\(=\cfrac{1}{a+jb}×\cfrac{a-jb}{a-jb}\)
\(=\cfrac{a-jb}{a^2+b^2}\)
\(=\cfrac{a}{a^2+b^2}-j\cfrac{b}{a^2+b^2}\)
のように、実数部と虚数部にすることができます。
複素数のまとめ
虚数は実在しない数なので、理解しづらいです。
しかし、虚数は存在すると仮定して計算に使うと便利なものです。
- 虚数とは、2乗して ー1になる数のこと。
- 複素数と共役複素数
- 複素数の四則演算
以上で「虚数とは何か?複素数の計算方法」の説明を終わります。