抵抗・コンデンサを直列に接続した「RC直列回路」の電圧、電流、インピーダンスの関係を説明します。
RC直列回路とRL直列回路の考え方は、コンデンサとコイルの違いだけで基本的には同じです。
RC直列回路の概要
RC直列回路とは、抵抗 R とコンデンサ C を、直列に接続した回路のことをいいます。

RC直列回路の電流
RC直列回路では、抵抗 \(R\) とコンデンサ \(C\) は
直列に接続されているので、RC直列回路に流れる電流 \(I\) は、同じ電流が流れます。
RC直列回路の電圧
抵抗の端子電圧 \(\dot{V_R}\) は
\(\dot{V_R}=R\dot{I}\) [V]
大きさは \(V_R=RI\) [V]
コンデンサの端子電圧 \(\dot{V_C}\) は
\(\dot{V_C}=X_C\dot{I}\) [V]
(\(X_C=\cfrac{1}{ωC}\)) なので
大きさは \(V_C=X_CI=\cfrac{I}{ωC}\) [V]
RC直列回路の全電圧 \(\dot{E}\) は抵抗とコイルの各端子電圧の和になります。
\(\dot{E}=\dot{V_R}+\dot{V_C}\) [V]
\(\dot{E}=(R+X_C)\dot{I}\) [V]
\(\dot{E}=(R+\cfrac{1}{ωC})\dot{I}\) [V]
大きさは \(E=I\sqrt{R^2+{X_C}^2}\) [V]
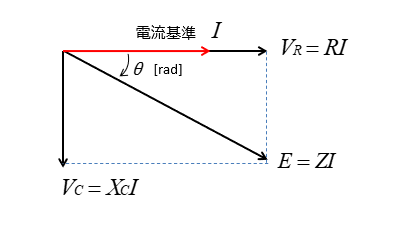
RC直列回路のベクトル図
RC直列回路のベクトルの描き方

RC直列回路では 流れる電流 \(\dot{I}\) が同じなので、電流を基準としてベクトルを描きます。
• 電流を基準ベクトルとして描きます。

抵抗の端子電圧 \(\dot{V_R}\) を電流と同相に描きます。
\(\dot{V_R}\) の長さは、矢印の始点からの長さです。
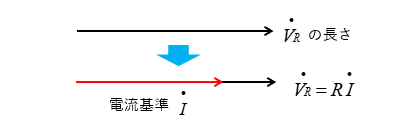
コンデンサの端子電圧 \(\dot{V_C}\) を電流より \(\cfrac{\pi}{2}\) 遅れて描きます。

\(\dot{V_R}\) と \(\dot{V_C}\) のベクトル和が電源電圧 \(\dot{E}\) になります。
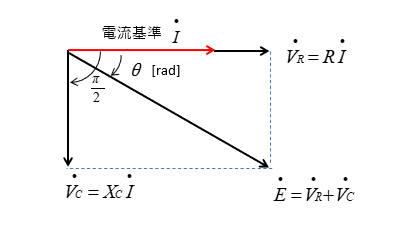
RC直列回路では、電源電圧に対して進み電流が流れます。
RC直列回路の電圧・電流の大きさ
■ RC直列回路の電圧・電流の大きさ
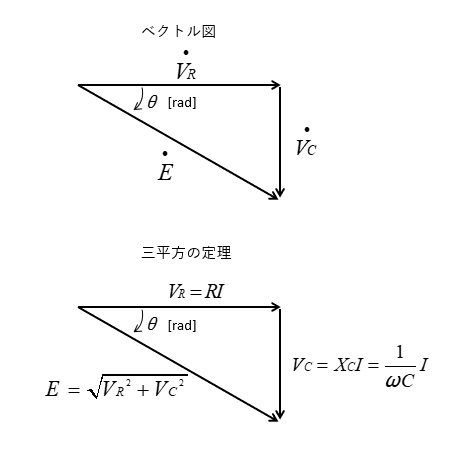
ベクトル図において \(\dot{V_R}\) \(\dot{V_C}\) \(\dot{E}\) は直角三角形ですから
三平方の定理を用いると回路の全電圧 \(E\) の大きさは
\(E=\sqrt{{V_R}^2+{V_C}^2}=\sqrt{(RI)^2+(X_CI)^2}\)
\(E=I\sqrt{R^2+{X_C}^2}\) [V]
\(E=I\sqrt{R^2+(\cfrac{1}{ωC})^2}\) [V]
したがって、回路に流れる電流 \(I\) は
\(I=\cfrac{E}{\sqrt{R^2+{X_C}^2}}\) [A]
\(I=\cfrac{E}{\sqrt{R^2+(\cfrac{1}{ωC})^2}}\) [A] になります。
RC直列回路の合成インピーダンスの大きさ
合成インピーダンスは 電圧と電流の比ですから
電圧の式
\(E=I\sqrt{R^2+{X_C}^2}\) [V] から
\(Z=\cfrac{E}{I}=\sqrt{R^2+{X_C}^2}\) [Ω]
\(X_C=\cfrac{1}{ωC}\) なので
\(Z=\sqrt{R^2+(\cfrac{1}{ωC})^2}\) [Ω] になります。
■ RC直列回路の合成インピーダンス角
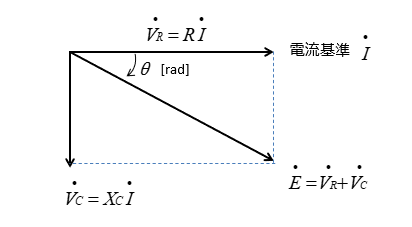
RC直列回路のベクトル図で、基準とする電流 \(\dot{I}\) に対する電圧 \(\dot{E}\) の位相差 \(θ\) を RC直列回路の インピーダンス角 といいます。
\(\tanθ=\cfrac{-V_C}{V_R}=\cfrac{-X_CI}{RI}=\cfrac{X_C}{R}\)
\(θ=\tan^{-1}\cfrac{-X_C}{R}\) [rad]
RC直列回路の記号法
交流を複素数で表す方法を 記号法 といいます。
次の回路は記号法によるRC直列回路です。
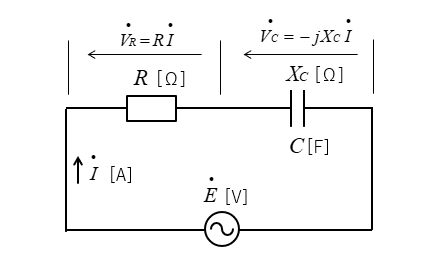
■ 直交座標表示
\(-jX_C=-j\cfrac{1}{ωC}=\cfrac{1}{jωC}\) 容量性リアクタンス
抵抗 \(R\) の端子電圧 \(\dot{V_R}\) は、電流 \(\dot{I}\) と同相なので
\(\dot{V_R}=R\dot{I}\) [V]
コンデンサ \(C\) の端子電圧 \(\dot{V_C}\) は電流 \(\dot{I}\) より、\(\cfrac{π}{2}\) [rad] 位相が遅れます。
\(\dot{V_C}=-jX_C\dot{I}=-j\cfrac{\dot{I}}{ωC}\) [V]
■ 虚数単位 \(j\) を付ける場所
- 虚数単位がややこしくなるのは、どこに付けたらいいかわからない。
- \(+j、-j\) どっちになるかわからない。ということではないでしょうか
■ 虚数単位 \(j\) は、\(ω\)(オメガ)の前に \(+j\) を付けると覚えましょう。
これを覚えれば、かなりの部分が解決すると思います。
- \(+j\) は反時計方向に90°移動します。
- \(-j\) は時計方向に90°移動します。

回路全体の電圧 \(\dot{E}\) は、RC直列回路では各端子電圧 \(\dot{V_R}\) と \(\dot{V_C}\) の和になりますから
\(\dot{E}=\dot{V_R}+\dot{V_C}\) [V]
\(\dot{E}=(R-jX_C)\dot{I}\) [V]
\(\dot{E}=(R-j\cfrac{1}{ωC})\dot{I}\) [V]
したがって、回路に流れる電流 \(\dot{I}\) は
\(\dot{I}=\cfrac{\dot{E}}{R-jX_C}\) [A]
\(\dot{I}=\cfrac{\dot{E}}{R-j\cfrac{1}{ωC}}\) [A] になります。
極座標表示

\(\dot{V_R}=R\dot{I}\angle 0\) [V] (電流 \(\dot{I}\) と同相)
\(\dot{V_C}=X_CI\angle -\cfrac{π}{2}\) [V] (電流 \(\dot{I}\) より \(\cfrac{π}{2}\) 遅れ)
\(\dot{E}\angle-θ(シータ)\) [V]
■ インピーダンスベクトル図
インピーダンスの関係を、図のように表したものを、インピーダンスベクトル図、または インピーダンス三角形 といいます。
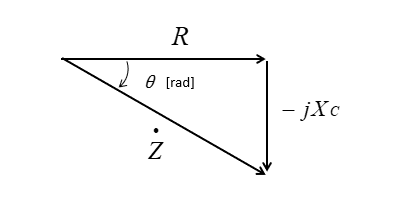
インピーダンス \(\dot{Z}\) は 電圧と電流の比ですから
\(\dot{E}=(R-jX_C)\dot{I}\) [V]
\(\dot{Z}=R-jX_C\) [Ω]
\(\dot{Z}=R-j\cfrac{1}{ωC}\) [Ω] になります。
■ インピーダンス角 \(θ\)
インピーダンスベクトル図から、インピーダンス角 \(θ\) [rad] は
\(θ=\tan^{-1}\cfrac{-X_C}{R}\) または
\(θ=\tan^{-1}\cfrac{-1}{ωCR}\) [rad] になります。
直列回路の力率について
直列回路の力率はインピーダンスで求めるときに
\(\cosθ=\cfrac{V_R}{E}=\cfrac{R}{Z}\) になります。
並列接続の力率は
\(\cosθ=\cfrac{Z}{R}\) になります。
RC直列回路の公式
■ RC直列回路の公式
ベクトル
\(X_C=\cfrac{1}{ωC}\) [Ω]
\(\dot{V_R}=R\dot{I}\) [V]
\(\dot{V_C}=X_C\dot{I}=\cfrac{\dot{I}}{ωC}\) [V]
\(\dot{E}=\dot{V_R}+\dot{V_C}\) [V]
記号法
\(-jX_C=\cfrac{1}{jωC}\) [Ω]
\(\dot{V_C}=-jX_C\dot{I}=\cfrac{\dot{I}}{jωC}\) [V]
\(\dot{E}=(R-jX_C)\dot{I}\) [V]
\(\dot{E}=(R-j\cfrac{1}{ωC})\dot{I}\) [V]
\(\dot{I}=\cfrac{\dot{E}}{R-jX_C}\) [A]
\(\dot{I}=\cfrac{\dot{E}}{R-j\cfrac{1}{ωC}}\) [A]
\(\dot{Z}=R-j\cfrac{1}{ωC}\) [Ω]
大きさ
\(E=\sqrt{{V_R}^2+{V_C}^2}\) [V]
\(E=I\sqrt{R^2+{X_C}^2}\) [V]
\(E=I\sqrt{R^2+{(\cfrac{1}{ωC}})^2}\) [V]
\(I=\cfrac{E}{\sqrt{R^2+{X_C}^2}}\) [A]
\(I=\cfrac{E}{\sqrt{R^2+{(\cfrac{1}{ωC})^2}}}\) [A]
\(Z=\sqrt{R^2+{X_C}^2}\) [Ω]
\(Z=\sqrt{R^2+(\cfrac{1}{ωC})^2}\) [Ω]
\(θ=\tan^{-1}\cfrac{-1}{ωCR}\) [rad]
練習問題
問題1
抵抗 4 [Ω] と容量性リアクタンス 3 [Ω] のコンデンサの直列回路がある。
この回路に、20 [V] の電圧を加えたとき回路に流れる電流 \(I\) の大きさを求めよ。
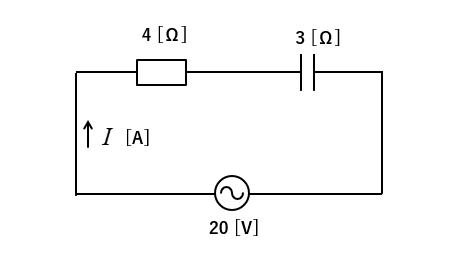
<解答例>
RC直列回路の合成インピーダンスは
\(Z=\sqrt{R^2+(X_C)^2}\) になります。
数値を当てはめると
\(Z=\sqrt{4^2+3^2}=5\) [Ω]
電流 \(I\) は次のように、求められます。
\(I=\cfrac{20}{5}=4\) [A]
以上で「RC直列回路の概要」の説明を終わります。