RLC回路の抵抗、コイル、コンデンサの電圧と電流の関係について説明します。
RLC直列回路とRLC並列回路のベクトル図の書き方や記号法による表示方法を説明します。
| RLC回路 | |
|---|---|
| 直列 | \(\dot{Z}=R\dot{I}+j(ωL-\cfrac{1}{ωC})\) |
| \(Z=\sqrt{R^2+(ωL-\cfrac{1}{ωC})^2}\) | |
| 並列 | \(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{jωL}+jωC}\) |
| \(\cfrac{1}{X_L}-\cfrac{1}{X_C}=\cfrac{1}{X}\) とすると \(Z=\cfrac{RX}{\sqrt{R^2+X^2}}\) | |
RLC回路
RLC回路は、抵抗(R)、コイル(L)、コンデンサ(C)を直列または並列に接続した回路のことです。
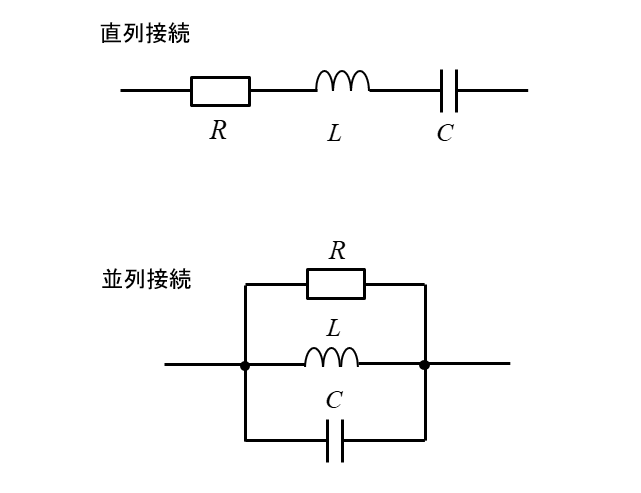
RLC回路は、直流電源に接続しても意味を持ちません。
RLC回路は、交流電源に接続した時に意味を持ちます。
RLC直列回路
RLC直列回路を交流電源に接続すると、抵抗(R)、コイル(L)、コンデンサ(C)の各素子は電流を妨げる働きをします。
- 抵抗は電流を妨げる
- コイルは誘導性リアクタンスとなり電流を妨げる
- コンデンサは容量製リアクタンスとなり電流を妨げる
- 抵抗とリアクタンスの合計をインピーダンスという
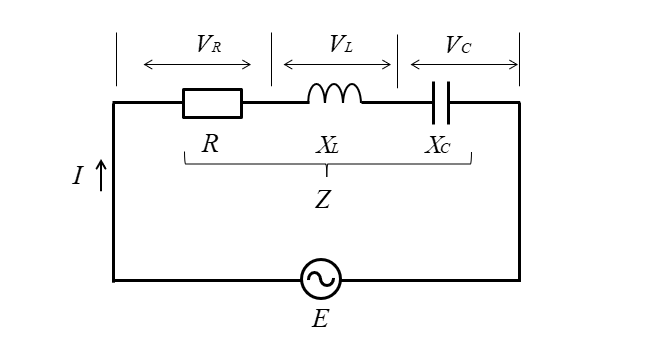
- リアクタンス
-
\(X_L\)はコイルの誘導性リアクタンス
\(X_C\)はコンデンサの容量性リアクタンス
- インピーダンス
-
\(Z\)は抵抗とリアクタンスを合計したもの
RLC直列回路では、各素子R、L、Cに流れる電流は共通しています。
電流が共通しているので、電流を基準にして、抵抗、コイル、コンデンサにかかる電圧を考えるとわかりやすい。
抵抗、コイル、コンデンサの電圧と電流の位相
抵抗の電圧と電流の位相
交流電源に抵抗を接続した回路では、電流と電圧は同相になります。
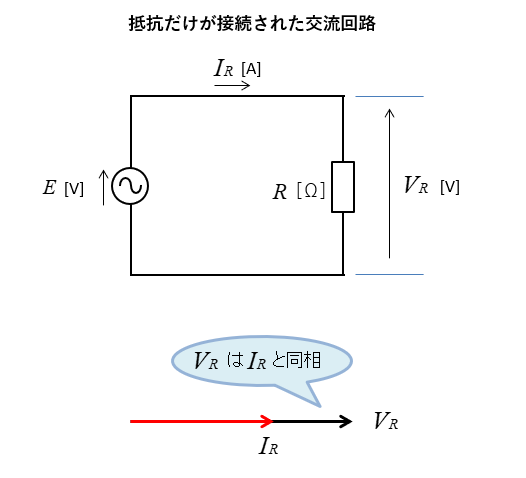
コイルの電圧と電流の位相
交流電源にコイルを接続した回路では、電圧が電流に対して \(\cfrac{π}{2}\) 進みます。
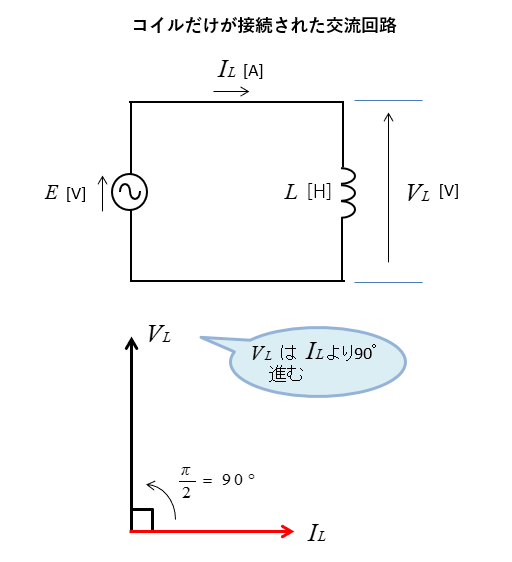
コンデンサの電圧と電流の位相
交流電源にコンデンサを接続した回路では、電圧が電流に対して \(\cfrac{π}{2}\) 遅れます。
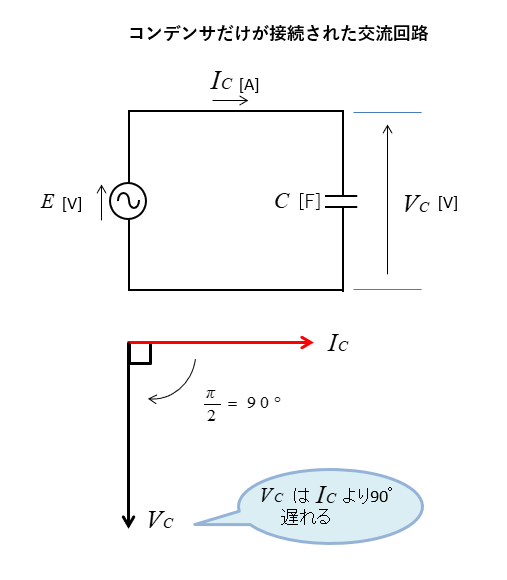
RLC直列回路と全体のベクトル図
電流 \(I\) に対する、\(V_R、V_L、V_C\) の関係です。
誘導性リアクタンスが大きい時
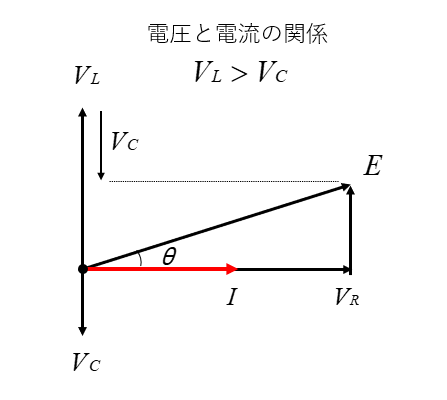
電圧と電流の関係 \(V_L>V_C\) の場合
電流に対して、電圧が \(θ\\) [rad] 進む。
容量性リアクタンスが大きい時
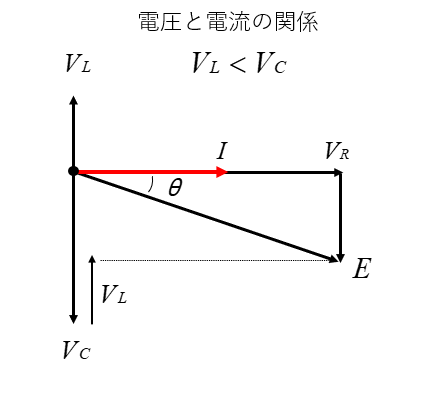
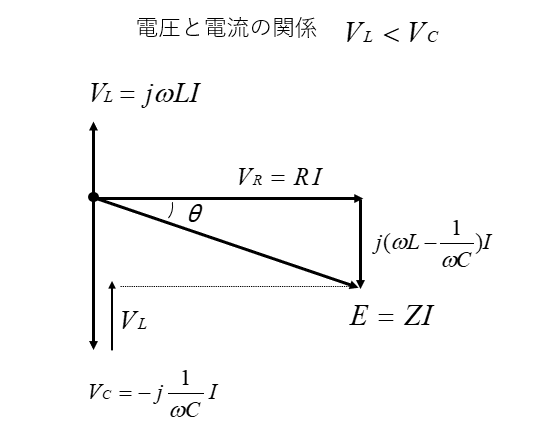
電圧と電流の関係 \(V_L<V_C\) の場合
電流に対して、電圧が \(θ\\) [rad] 遅れる。
RLC直列回路の記号法表示

RLC直列回路の電圧と電流
RLC直列回路の記号法によるベクトル図は、次のようになります。
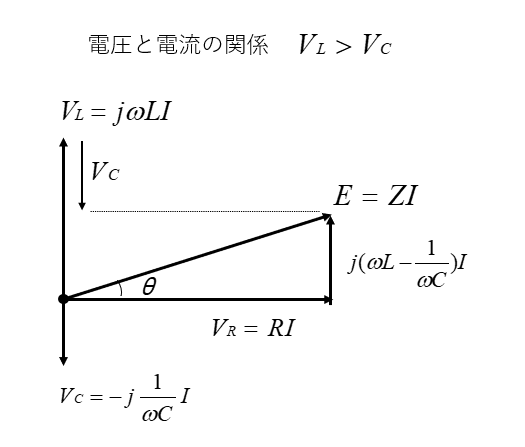
電圧
電圧は抵抗、コイル、コンデンサの、端子電圧のベクトル和になります。
\(\dot{E}=\dot{V_R}+\dot{V_L}+\dot{V_C}\)
\(\dot{V_R}=R\dot{I}\)
\(\dot{V_L}=jX_L\dot{I}\)
\(\dot{V_C}=-jX_C\dot{I}\)
上の式に代入すると
\(\dot{E}=R\dot{I}+j(X_L-X_C)\dot{I}=\dot{Z}\dot{I}\)
\(X_L=ωL\)
\(X_C=\cfrac{1}{ωC}\)
\(\dot{E}=R\dot{I}+j(ωL-\cfrac{1}{ωC})\dot{I}\)
RLC直列回路の電流
\(\dot{I}=\cfrac{\dot{E}}{R+j(ωL-\cfrac{1}{ωC})}\)\(=\cfrac{\dot{E}}{\dot{Z}}\)
インピーダンスベクトル
RLC直列回路図において、インピーダンスベクトルは次のようになります。
誘導性リアクタンスが大きい時
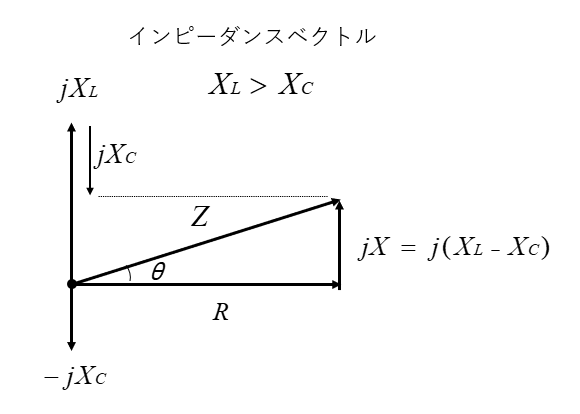
RLC直列回路のインピーダンス
\(\dot{Z}=R+j(X_L-X_C)\)
インピーダンスの大きさ
\(Z=\sqrt{R^2+(X_L-X_C)^2}\)
ここで
\(X_L=jωL\)
\(X_C=\cfrac{1}{jωC}\)
とすると、インピーダンスは
\(\dot{Z}=(R+jωL-j\cfrac{1}{ωC})\)
インピーダンスの大きさは
\(Z=\sqrt{R^2+(ωL-\cfrac{1}{ωC})^2}\)
容量性リアクタンスが大きい時
容量性リアクタンスが大きい時も、数式を変える必要はありません。
- \(j\) の符号は、ベクトルの方向を示している
- ベクトルの大きさは、2乗したものの平方根になるので問題ない
\(\dot{E}=\dot{V_R}+\dot{V_L}+\dot{V_C}\)
\(\dot{V_R}=R\dot{I}\)
\(\dot{V_L}=jX_L\dot{I}\)
\(\dot{V_C}=-jX_C\dot{I}\)
上の式に代入すると
\(\dot{E}=R\dot{I}+j(X_L-X_C)\dot{I}=\dot{Z}\dot{I}\)
\(X_L=ωL\)
\(X_C=\cfrac{1}{ωC}\)
\(\dot{E}=R\dot{I}+j(ωL-\cfrac{1}{ωC})\dot{I}\)
RLC直列回路の電流
\(\dot{I}=\cfrac{\dot{E}}{R+j(ωL-\cfrac{1}{ωC})}\)\(=\cfrac{\dot{E}}{\dot{Z}}\)
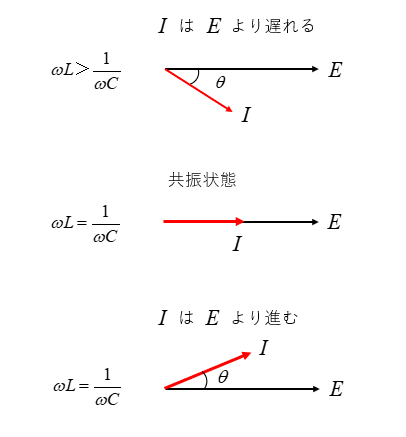
電圧と電流の位相関係
RLC直列回路の位相関係は、\(ωL\) と \(\cfrac{1}{ωC}\) の大きさによって、図 のようになります。
\(ωL=\cfrac{1}{ωC}\) のときは、共振状態 と言われます。
RLC並列回路
RLC直列回路を交流電源に接続すると、抵抗(R)、コイル(L)、コンデンサ(C)の各素子は電流を妨げる働きをします。
- 抵抗は電流を妨げる
- コイルは誘導性リアクタンスとなり電流を妨げる
- コンデンサは容量製リアクタンスとなり電流を妨げる
- 抵抗とリアクタンスの合計をインピーダンスという
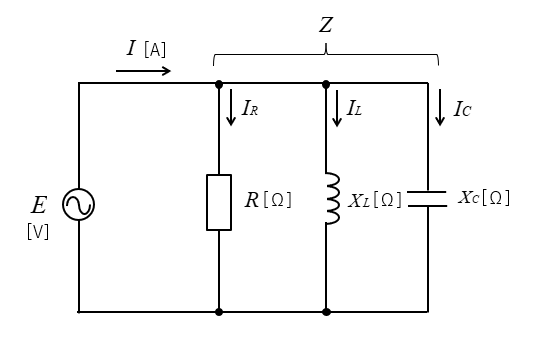
RLC並列回路では、各素子 R、L、C にかかる「電圧」が同じです。
電圧を基準にして、抵抗、コイル、コンデンサに流れる「電流」を考えるとわかりやすい。
- リアクタンス
-
\(X_L\)はコイルの誘導性リアクタンス
\(X_C\)はコンデンサの容量性リアクタンス
- インピーダンス
-
\(Z\)は抵抗とリアクタンスを合計したもの
RLC並列回路の電圧と電流の関係
抵抗の電圧と電流の位相
交流電源に抵抗を接続した回路では、電流と電圧は同相になります。

コイルの電圧と電流の位相
交流電源にコイルを接続した回路では、電圧が電流に対して \(\cfrac{π}{2}\) 進みます。

コンデンサの電圧と電流の位相
交流電源にコンデンサを接続した回路では、電圧が電流に対して \(\cfrac{π}{2}\) 遅れます。

RLC並列回路と全体のベクトル図
図は電圧 \(E\) に各 \(I_R、I_L、I_C\) の関係を表示したものです。
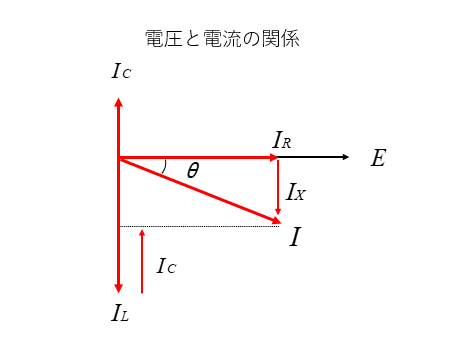
電圧と電流の関係 \(I_L>I_C\) の場合
電源電圧に対して、電流の位相が \(θ\quad\rm[rad]\) 遅れていることを示しています。
RLC並列回路の記号法表示

RLC並列回路において
\(\dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}\)
\(\dot{I}=\cfrac{\dot{E}}{R}+\cfrac{\dot{E}}{jωL}+\cfrac{\dot{E}}{\cfrac{1}{jωC}}\)
\(\dot{I}=\dot{E}\left(\cfrac{1}{R}+\cfrac{1}{jωL}+jωC\right)\)
\(\dot{Z}=\cfrac{\dot{E}}{\dot{I}}\)\(=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{jωL}+jωC}\)
RLC並列回路の合成インピーダンス
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{jωL}+jωC}\) [Ω]

アドミタンス \(Y\) で表すと次のようになる。
\(Y=\cfrac{1}{Z}\)\(=\cfrac{1}{R}+\cfrac{1}{jωL}+jωC\) [S]
電流 \(I\) はアドミタンス \(Y\) を使うと次のようになる。
\(I=E × Y\) [A]

以上で「RLC回路(直列と並列)」の説明を終わります。