RLC並列回路の共振についての説明です。
どのような条件になると、RLC並列回路が共振状態になるのか?
共振周波数の求め方や共振状態のときの、「電圧、電流、インピーダンス」について説明します。
| RLC共振回路 | |
|---|---|
| 直列共振条件 | \(ωL=\cfrac{1}{ωC}\) |
| 並列共振条件 | \(\cfrac{1}{ωL}=ωC\) |
| 共振周波数 | \(f_0=\cfrac{1}{2π\sqrt{LC}}\) [Hz] |
RLC直列共振については、こちらの記事が参考になります。
RLC並列共振とは何のこと?
RLC並列回路 と RLC並列共振回路です。
見たところ違いはありませんね。
実は、回路の周波数が違います。
RLC並列回路のある特別な状態の時をRLC並列共振回路といいます。
コイルのリアクタンスは
\(X_L=ωL=2πfL\)
コンデンサのリアクタンスは
\(X_C\)\(=\cfrac{1}{ωC}\)\(=\cfrac{1}{2πfC}\) です。
両方とも、周波数 \(f\) が関係しています。
RLC並列回路のインピーダンスの式は、次のようになります。
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)}\) [Ω]
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{ωL}-ωC\right)}\) [Ω]\(\cdots(1)\)
RLC並列回路の ある特別な状態の時 は何かというと
式(1)の虚数部 \(\left(\cfrac{1}{ωL}-ωC\right)\) が
\(\left(\cfrac{1}{ωL}-ωC\right)=0\) になるときのことです。
RLC並列共振
共振とは”RLC並列回路において、\(\left(\cfrac{1}{ωL}=ωC\right)\) になるときの状態を共振状態といいます。
共振状態のときのインピーダンスは、\(Z=R\) となり、抵抗 \(R\) だけになります。
\(\left(\cfrac{1}{ωL}-ωC\right)=0\) になるということは、どういうことかというと
見かけ上、コイルとコンデンサがなくなったということになります。
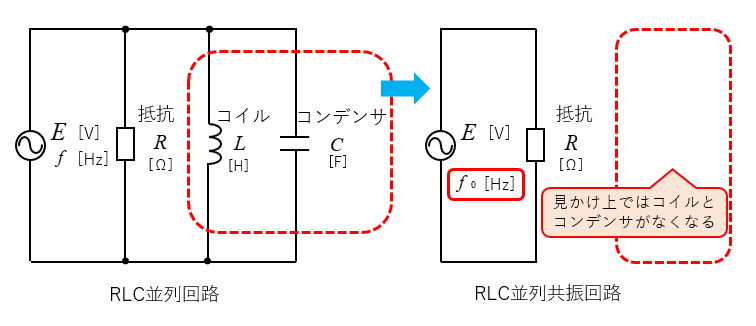
RLC並列回路において、\(\left(\cfrac{1}{ωL}=ωC\right)\) になることを RLC並列共振 といいます。
共振はある特定の周波数のときに \(\left(\cfrac{1}{ωL}=ωC\right)\) という状態になります。
このときの周波数を 共振周波数 \(f_0\) といいます。
共振周波数 \(f_0\) のときの、インピーダンスの式は \(\left(\cfrac{1}{ωL}-ωC\right)=0\) なので
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{ωL}-ωC\right)}\) [Ω]
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+0}\) [Ω]
\(\dot{Z}=R\) [Ω] になります。
コイルとコンデンサが共振したときの、インピーダンス
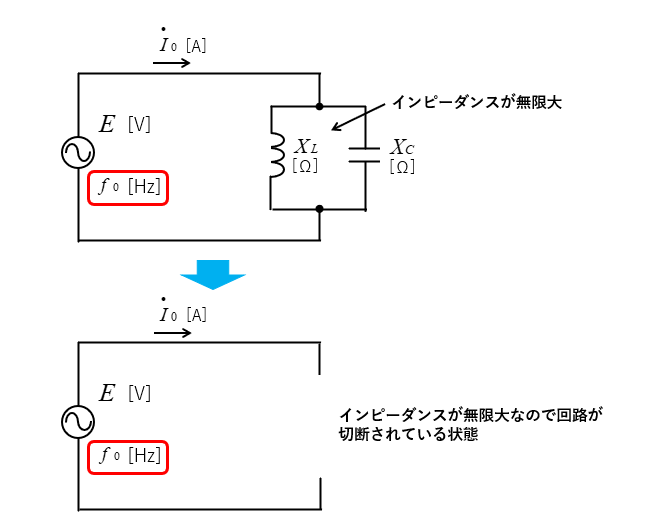
コイルとコンデンサだけの回路が共振したときのインピーダンス \(\dot{Z}\) を考えてみましょう。
\(Z=\cfrac{1}{\cfrac{1}{ωL}-ωC}=\cfrac{1}{0}=∞\) [Ω]
インピーダンスが無限大ということは、回路に電流が流れませんから回路が切断されているのと同じ状態になります。
RLC並列共振回路の共振周波数
RLC並列回路の共振周波数 \(f_0\) は、共振角速度を \(ω_0\) とすると
\(\cfrac{1}{ωL}=ωC\) から
\(ω^2=\cfrac{1}{LC}\)
\(ω=\cfrac{1}{\sqrt{LC}}\)
ここで、\(ω_0=2πf\) ですから
\(2πf_0=\cfrac{1}{\sqrt{LC}}\) になります。
したがって、共振周波数は
\(f_0=\cfrac{1}{2π\sqrt{LC}}\) [Hz] になります。
RLC並列共振時の電流
RLC並列共振時に抵抗、コイル、コンデンサに流れる電流は、図のようになります。

共振しているときは、コイルの電流 \(I_L\) とコンデンサの電流 \(I_C\) が互いに打ち消し合うのでリアクタンス分はなくなり、抵抗分だけになります。
■ 各素子に流れる電流
抵抗 \(R\) の電流 \(I_R\) は
\(I_R=\cfrac{E}{R}\) [A]
コイルに流れる電流 \(I_L\) は
\(I_L=\cfrac{E}{jωL}\) [A]
コンデンサに流れる電流 \(I_C\) は
\(I_C=jωCE\) [A]
全電流 \(I\) は
\(I=I_R+I_L+I_C\)
\(I\)\(=\cfrac{E}{R}+\cfrac{E}{jωL}+jωCE\) [A]
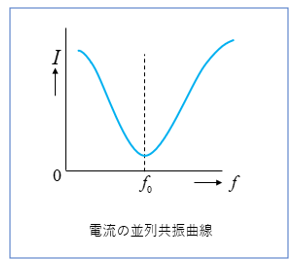
■ RLC並列共振時の電流
RLC並列回路の共振状態のときには、図のように共振電流 \(I_0\) は最小になります。
共振電流 \(I_0\) は
\(I_0\)\(=\cfrac{E}{Z}\)\(=\cfrac{E}{R}\quad[\rm A]\) になります。
練習問題
問題1
抵抗 \(R=4\) [Ω]、コイル \(L=2\) [H]、コンデンサ \(C=5.07\) [uF] を図のように接続した回路の共振周波数 \(f_0\) を求めよ。
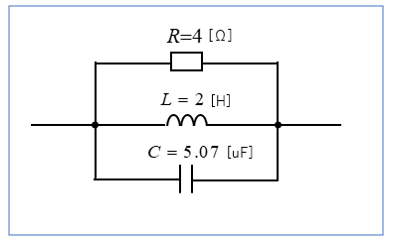
<解答例>
\(f_0=\cfrac{1}{2π\sqrt{LC}}\)\(=\cfrac{1}{2×3.14×\sqrt{2×5.07×10^{-6}}}\)
\(f_0=\cfrac{1}{6.28×\sqrt{10.14×10^{-6}}}\)\(≒\cfrac{1}{6.28×3.18×10^{-3}}≒50\) [Hz]
以上で「RLC並列共振回路」の説明を終わります。