RLC直列回路の共振についての説明です。
どのような条件になると、RLC直列回路が共振状態になるのか?
共振周波数の求め方や共振状態のときの、「電圧、電流、インピーダンス」について説明します。
| RLC共振回路 | |
|---|---|
| 直列共振条件 | \(ωL=\cfrac{1}{ωC}\) |
| 並列共振条件 | \(\cfrac{1}{ωL}=ωC\) |
| 共振周波数 | \(f_0=\cfrac{1}{2π\sqrt{LC}}\) [Hz] |
RLC並列共振については、こちらの記事が参考になります。
RLC直列共振とは何のこと?
RLC直列回路 と RLC直列共振回路です。
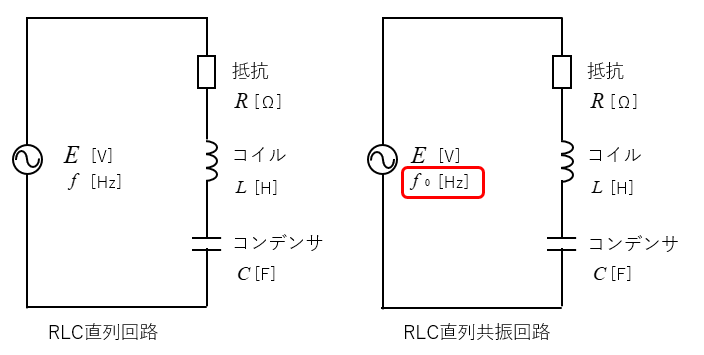
見たところ違いはありませんね。
実は、回路の周波数が違います。
RLC直列回路のある特別な状態の時をRLC直列共振回路といいます。
共振という現象には、リアクタンスが関係しています。
コイルのリアクタンスは
\(X_L=ωL=2πfL\)
コンデンサのリアクタンスは
\(X_C=\cfrac{1}{ωC}=\cfrac{1}{2πfC}\) です。
両方とも、周波数 \(f\) が関係しています。
RLC直列回路のインピーダンスの式は、次のようになります。
\(Z=R+j(X_L-X_C)\)\(=R+j(ωL-\cfrac{1}{ωC})\cdots(1)\)
RLC直列回路のある特別な状態の時は何かというと
式(1)の虚数部 \((ωL-\cfrac{1}{ωC})\) が
\((ωL-\cfrac{1}{ωC})=0\) になるときのことです。
\((ωL-\cfrac{1}{ωC})=0\) になるということは、どういうことかというと
見かけ上、コイルとコンデンサがなくなったということになります。
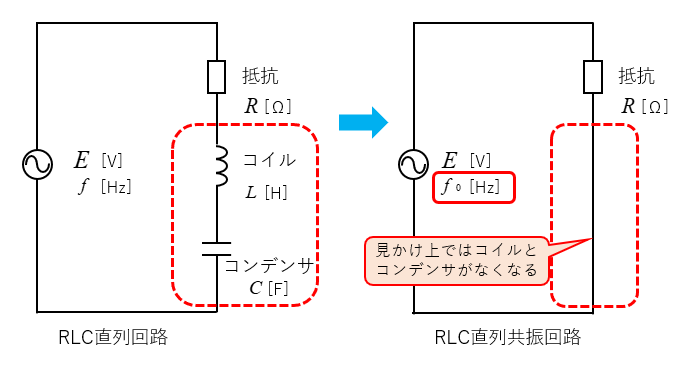
直列共振のとき
コイルとコンデンサがなくなったと言うと
回路が切れたように感じるかもしれませんが
コイルとコンデンサのリアクタンスが打ち消し合ってゼロになり導通(短絡)したと考えると良いでしょう。
並列共振のとき
並列共振のときも、コイルとコンデンサのリアクタンスが
打ち消し合ってゼロになるのは直列共振と同じです。
合成リアクタンス自体は無限大になりますので
回路が切断された状態になります。
ここが直列共振と異なるところです。
RLC直列回路において、\((ωL=\cfrac{1}{ωC})\) になることをRLC直列共振といいます。
共振はある特定の周波数のときに \((ωL=\cfrac{1}{ωC})\) という状態になります。
このときの周波数を共振周波数 \(f_0\) といいます。
共振周波数 \(f_0\) のときの、
ンピーダンスの式は
\((ωL-\cfrac{1}{ωC})=0\) なので
\(Z=R+j(ωL-\cfrac{1}{ωC})\)
\(Z=R\cdots(2)\) になります。
RLC直列共振
- 共振とは”RLC直列回路において、\(ωL=\cfrac{1}{ωC}\) になるときの状態を共振状態といいます。
- 共振状態のときのインピーダンスは、\(Z=R\) となり、抵抗 \(R\) だけになります。
RLC直列共振回路の共振周波数
RLC直列回路のリアクタンスと周波数の関係を、グラフで見ると次のようになります。
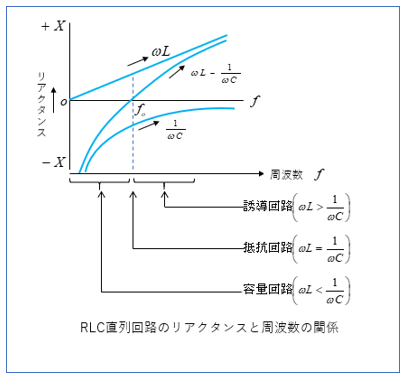
コイルのリアクタンス \(ωL\) は周波数に比例して大きくなります。
逆に、コンデンサのリアクタンス \(\cfrac{1}{ωC}\) は反比例して小さくなります。
コイルのリアクタンスとコンデンサのリアクタンスは
正反対の性質があるので周波数を増加させていくと途中に必ず
\((ωL=\cfrac{1}{ωC})\) になり共振する周波数があります。
このように共振したときの周波数 \(f_0\) を共振周波数といいます。
共振周波数 \(f_0\) のときの共振角速度を \(ω_0\) とすると
\(ω_0L=\cfrac{1}{ω_0C}\) から
\({ω_0}^2=\cfrac{1}{LC}\)
\(ω_0=\cfrac{1}{\sqrt{LC}}\)
ここで、\(ω_0=2πf_0\) ですから
\(2πf_0=\cfrac{1}{\sqrt{LC}}\) になります。
したがって、共振周波数は
\(f_0=\cfrac{1}{2π\sqrt{LC}}\) [Hz] になります。
RLC直列共振時の電圧
RLC直列共振時に抵抗、コイル、コンデンサの端子電圧は、図のようになります。
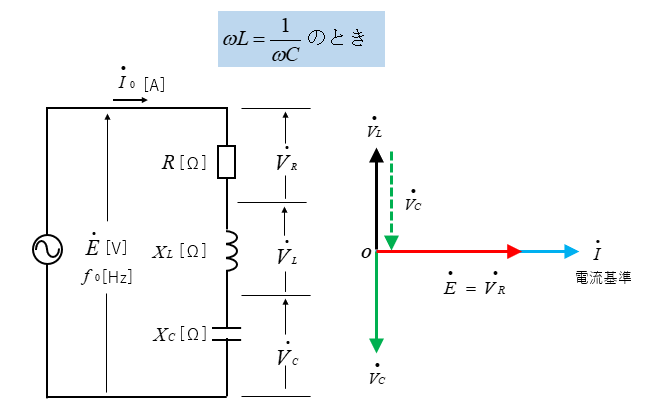
共振しているときは、コイルの端子電圧 \(V_L\) と コンデンサの端子電圧 \(V_C\) が互いに打ち消し合うのでリアクタンス分はなくなり、抵抗分だけになります。
また、共振時に流れる電流を共振電流 \(I_0\) といいます。
共振電流 \(I_0\) は、共振時に最大になります。
\(I_0=\cfrac{E}{Z}\)\(=\cfrac{E}{R}\) [A]
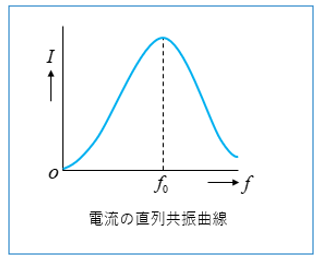
共振時の電流が最大になる
\(I=\cfrac{E}{Z}\) [A]
\(Z=R+X\) [Ω]
\(X=0\) のとき \(Z=R\) [Ω] でインピーダンスが最小になるので、電流は最大になります。
\(X\neq0\) のとき \(Z=R+X\) [Ω] で \(Z=R\) [Ω] より大きくなるので、電流は最大値より必ず小さくなります。
インピーダンスベクトル図
次に共振時とそれ以外のときのインピーダンスを、ベクトルで表すと次のようになります。
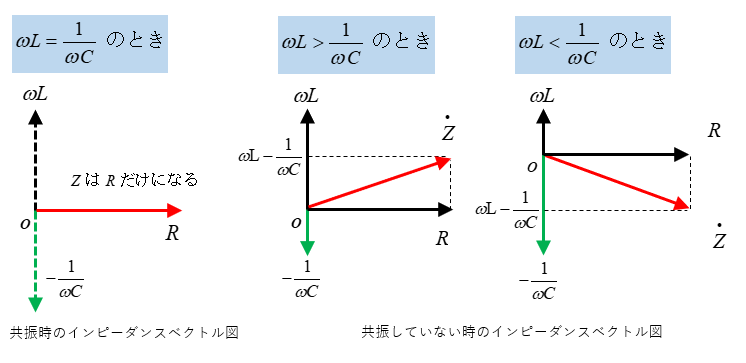
RLC直列共振回路の特徴
共振状態の場合
- 電源から見たインピーダンスは見かけ上は抵抗だけになるので、電圧と電流は同相になります。
- 共振状態のときは L や C の端子電圧が電源電圧より大きくなります。
電圧拡大作用という現象が起こります。 - 共振状態のときの電流の値は最大になります。
\(L\) と \(C\) の電圧拡大作用
RLC直列回路が共振状態になると、電源電圧 \(E\) より \(L\) や \(C\) の端子電圧が大きくなるという現象が起こります。
その大きさは、共振電流を \(I_0\) とすると
\(I_0=\cfrac{E}{R}\) [A]
共振角速度 \(ω_0\) は
\(ω_0=\cfrac{1}{\sqrt{LC}}\)
\(L\) や \(C\) の端子電圧 \(V_L、V_C\) は次のようになります。
\(V_L=ω_0LI_0\)\(=ω_0L\cfrac{E}{R}\) [V]
\(V_C=\cfrac{1}{ω_0C}I_0\)\(=\cfrac{1}{ω_0C}\cfrac{E}{R}\) [V]
電源電圧と \(V_L\) や \(V_C\) の比を選択度といい、\(Q\) を使います。
\(Q=\cfrac{V_L}{E}\)\(=\cfrac{ω_0L\cfrac{E}{R}}{E}\)\(=\cfrac{ω_0L}{R}\)\(=\cfrac{1}{R}\sqrt{\cfrac{L}{C}}\)
\(Q=\cfrac{V_C}{E}\)\(=\cfrac{\cfrac{E}{ω_0CR}}{E}\)\(=\cfrac{1}{ω_0CR}\)\(=\cfrac{1}{R}\sqrt{\cfrac{L}{C}}\)
したがって、\(L\) や \(C\) は電源電圧に対して
\(L\) の端子電圧は \(\cfrac{ωL}{R}\) 倍
\(C \) の端子電圧は \(\cfrac{1}{ωCR}\) 倍 になります。
選択度 \(Q\) は
\(Q=\cfrac{V_L}{E}\)\(=\cfrac{V_C}{E}\)\(=\cfrac{1}{R}\sqrt{\cfrac{L}{C}}\) になります。
練習問題
問題1
次のようなRLC直列回路に
\(R=10\) [Ω]、 \(L=10π\) [mH]、 \(C=\cfrac{π}{4}\) [μF] が
接続されているとき、\(E=10\) [V] の交流電圧を加えると
共振時に \(L、C\) 両端の電圧は 何 [V] になるか求めよ。
(\(π^2 \fallingdotseq 10\)とする。)
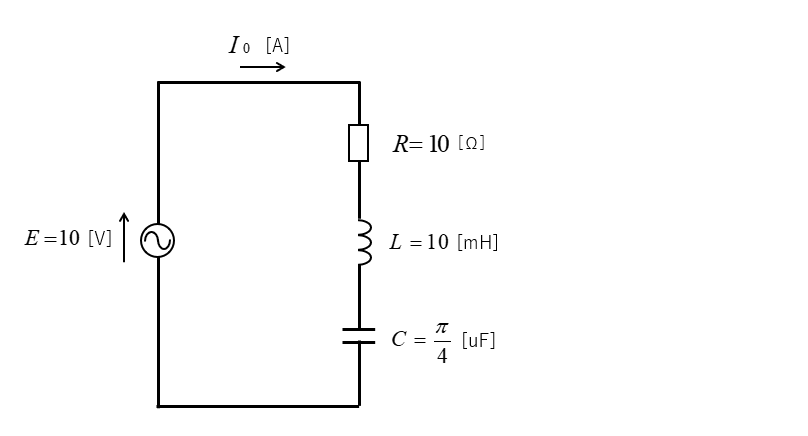
<解答例>
共振周波数の公式から、共振周波数を求めます。
\(f_0=\cfrac{1}{2π\sqrt{LC}}\)
\(=\cfrac{1}{2π\sqrt{10π×10^{-3}×(π/4)×10^{-6}}}\)
\(=\cfrac{1}{π^2×10^{-4}}\)
\(f_0=\cfrac{10000}{10}=1000\) [Hz]
共振時にはインピーダンスが抵抗だけになるので共振電流が求められます。
\(I_0=\cfrac{E}{Z}=\cfrac{E}{R}=\cfrac{10}{10}=1\) [A]
共振時の誘導性リアクタンスは
\(X_L=ωL=2πfL\)\(=2π×10^3×10π×10^{-3}=200\) [Ω]
共振時の容量性リアクタンスは
\(X_C=\cfrac{1}{ωC}=\cfrac{1}{2πfC}\)
\(=\cfrac{1}{2π×10^3×(π/4)×10^{-6}}\)\(=200\) [Ω]
• コイルの端子電圧は
\(V_L=ωLI=200×1=200\) [V]
• コンデンサの端子電圧は
\(V_C=\cfrac{1}{ωC}I=200×1=200\) [V]
\(Q=\cfrac{ωL}{R}\)\(=\cfrac{200}{10}=20\) 倍
\(Q=\cfrac{1}{ωCR}\)\(=200×\cfrac{1}{10}=20\) 倍
このことから分かるように、\(L\) や \(C\) の端子電圧は電源電圧の \(20\) 倍になることが分かります。
RLC回路(直列と並列)
RLC並列共振回路
RL直列回路の概要
RC直列回路の概要
RLC直列回路の説明
RL並列回路の概要
RC並列回路の概要
RLC並列回路の説明