抵抗とコイルとコンデンサを並列に接続した「RLC並列回路」の、電圧、電流、インピーダンスの関係について説明します。
RLC並列回路はコイルとコンデンサが、反対の性質を持つので回路の解析が複雑になります。
RLC並列回路の説明
RLC並列回路とは、抵抗 \(R\) 、コイル \(L\) 、コンデンサ \(C\) を、並列に接続した回路のことです。

■ RLC並列回路の電圧
RLC並列回路では、抵抗 \(R\) 、コイル \(L\) 、コンデンサ \(C\) は、並列に接続されているので、RLCにかかる電圧 \(\dot{E}\) は同じ大きさの電圧になります。
■ 各枝路に流れる電流の大きさ
\(I_R=\cfrac{E}{R}\) [A] (抵抗に流れる電流)
\(I_L=\cfrac{E}{X_L}=\cfrac{E}{ωL}\) [A] (コイルに流れる電流)
\(I_C=\cfrac{E}{X_C}=\cfrac{E}{\cfrac{1}{ωC}}=ωCE\) [A] (コンデンサに流れる電流)
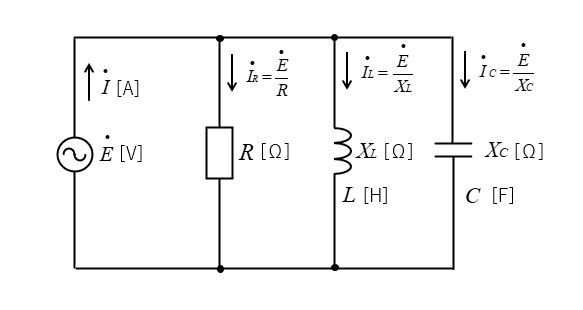
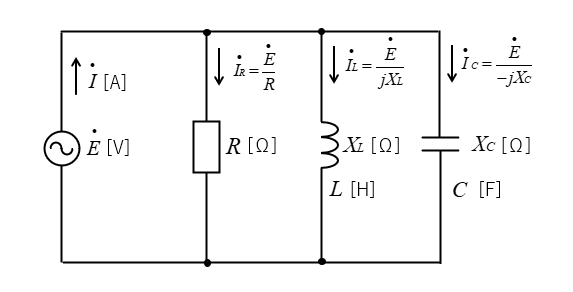
RLC並列回路に交流電源 \(\dot{E}\) を接続したとき、RLC並列回路にかかる電圧を \(\dot{E}\) 抵抗、コイル、コンデンサに流れる電流を \(\dot{I_R}\) \(\dot{I_L}\) \(\dot{I_C}\) とします。
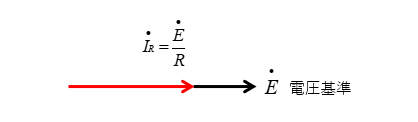
■ 抵抗に流れる電流
\(\dot{I_R}=\cfrac{\dot{E}}{R}\) は電圧 \(\dot{E}\) と 同相 になります。
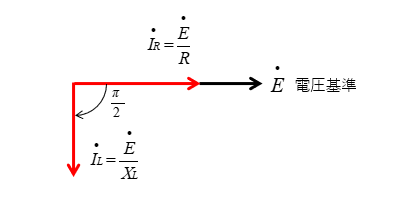
■ コイルに流れる電流
\(\dot{I_L}=\cfrac{\dot{E}}{X_L}\) は電圧 \(\dot{E}\) より \(\cfrac{\pi}{2}\) 位相が 遅れ ます。
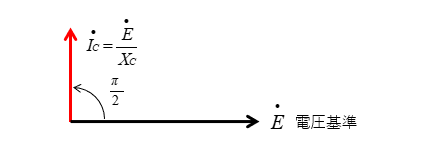
■ コンデンサに流れる電流
\(\dot{I_C}=\cfrac{\dot{E}}{X_C}\) は電圧 \(\dot{E}\) より \(\cfrac{\pi}{2}\) 位相が 進み ます。
■ 回路に流れる電流
回路に流れる全電流 \(\dot{I}\) は 並列接続なので、各枝路に流れる電流の ベクトルの和 になります。
\(\dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}\) [A]
■ RLC並列回路のリアクタンスの組み合わせ
誘導性リアクタンス \(X_L\) と容量性リアクタンス \(X_C\) の大きさにより、次の三つの組み合わせができます。
- \(X_L>X_C\)\(\cdots\)誘導性リアクタンス>容量性リアクタンス
- \(X_L<X_C\)\(\cdots\)誘導性リアクタンス<容量性リアクタンス
- \(X_L=X_C\)\(\cdots\)誘導性リアクタンス=容量性リアクタンス
③ の場合を 「共振状態」 といいます。
XL>XC のときのRLC並列回路
\(X_L>X_C\) のときの、RLC並列回路について説明します。
■ \(X_L>X_C\) のときのRLC並列回路のベクトル
抵抗 \(R\) に流れる電流 \(I_R\) は、電圧 \(E\) と同相になります。

コイルに流れる電流 \(I_L\) は、電圧 \(E\) より位相が \(\cfrac{π}{2}\) 遅れます。

コンデンサに流れる電流 \(I_C\) は、電圧 \(E\) より位相が \(\cfrac{π}{2}\) 進みます。
\(X_L>X_C\) なので \(I_L<I_C\) になり、コンデンサに流れる電流のほうがコイルに流れる電流より大きくなります。
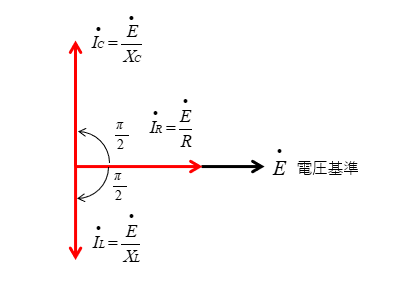
合成リアクタンス \(X\) は \(X_L>X_C\) ですから \(X=X_L-X_C\) になり 誘導性リアクタンス になります。
■ \(X_L>X_C\) のときの電流の合成ベクトル
RLC並列回路のベクトル関係は次のようになります。
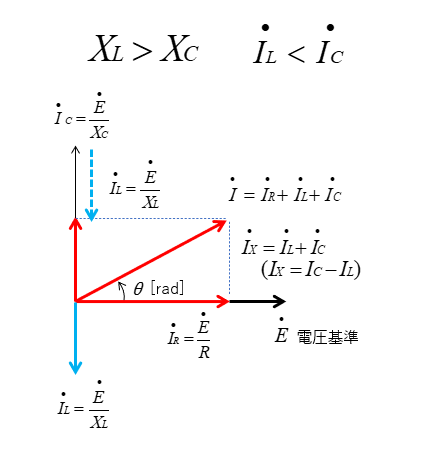
リアクタンスの電流を合成した \(\dot{I_X}\) は
\(\dot{I_X}=\dot{I_C}+\dot{I_L}\)\(=\cfrac{\dot{E}}{X_C}+\cfrac{\dot{E}}{X_L}\)
\(\dot{I_X}=\dot{E}\left(\cfrac{1}{X_C}+\cfrac{1}{X_L}\right)\) [A]
また、\(I_X\) の大きさは
\(I_X=I_C-I_L=E\left(\cfrac{1}{X_C}-\cfrac{1}{X_L}\right)\) [A] になります。
全電流 \(\dot{I}\) は \(\dot{I_R}\) と \(\dot{I_X}\) の合成になります。
\(\dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}\) [A]
全電流 \(I\) の大きさは、三平方の定理から
\(I=\sqrt{{I_R}^2+{I_X}^2}=\sqrt{{I_R}^2+(I_C-I_L)^2}\)
\(I=\sqrt{\left(\cfrac{E}{R}\right)^2+\left(ωCE-\cfrac{E}{ωL}\right)^2}\)
\(I=E\sqrt{\left(\cfrac{1}{R}\right)^2+\left(ωC-\cfrac{1}{ωL}\right)^2}\) [A]
■ \(X_L>X_C\) のときの合成インピーダンス

合成インピーダンス \(Z\) は
\(I=E\sqrt{\left(\cfrac{1}{R}\right)^2+\left(ωC-\cfrac{1}{ωL}\right)^2}\) [A] の式より
\(Z=\cfrac{E}{I}\)
\(Z=\cfrac{1}{\sqrt{\left(\cfrac{1}{R}\right)^2+\left(ωC-\cfrac{1}{ωL}\right)^2}}\) [Ω] になります。
■ \(X_L>X_C\) のときのインピーダンス角 θ
インピーダンス角 θ の大きさは
\(θ=\tan^{-1}\cfrac{\cfrac{1}{X_C}-\cfrac{1}{X_L}}{\cfrac{1}{R}}\)
\(θ=\tan^{-1}R\left(ωC-\cfrac{1}{ωL}\right)\) [rad]
■ 極座標表示

\(\dot{I_R}=\cfrac{\dot{E}}{R}\angle 0\) [A] (電圧 \(\dot{E}\) と同相)
\(\dot{I_L}=\cfrac{\dot{E}}{X_L}\angle -\cfrac{π}{2}\) [A] (電圧 \(\dot{E}\) より \(\cfrac{π}{2}\) 遅れ)
\(\dot{I_C}=\cfrac{\dot{E}}{X_C}\angle \cfrac{π}{2}\) [A] (電圧 \(\dot{E}\) より \(\cfrac{π}{2}\) 進み)
\(\dot{I}\angle+θ(シータ)\) [V]
XL<XC のときのRLC並列回路
\(X_L<X_C\) のときの、RLC並列回路について説明します。
■ \(X_L<X_C\) のときのRLC並列回路のベクトル
抵抗 \(R\) に流れる電流 \(I_R\) は、電圧 \(E\) と同相になります。

コイルに流れる電流 \(I_L\) は、電圧 \(E\) より位相が \(\cfrac{π}{2}\) 遅れます。
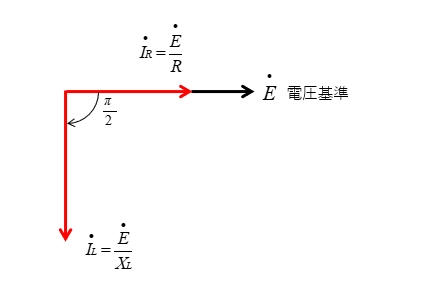
コンデンサに流れる電流 \(I_C\) は、電圧 \(E\) より位相が \(\cfrac{π}{2}\) 進みます。
\(X_L<X_C\) なので \(I_L>I_C\) になり、コイルに流れる電流のほうがコンデンサに流れる電流より大きくなります。
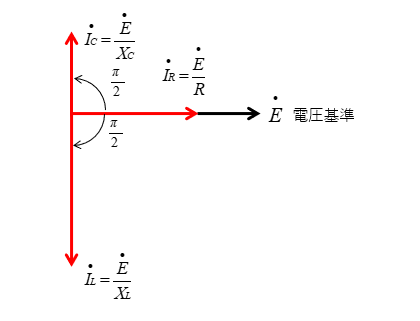
合成リアクタンス \(X\) は \(X_L<X_C\) ですから \(X=X_C-X_L\) になり 容量性リアクタンス になります。
■ \(X_L<X_C\) のときの電流の合成ベクトル
RLC並列回路のベクトル関係は次のようになります。

リアクタンス電流を合成した \(\dot{I_X}\) は
\(\dot{I_X}=\dot{I_L}+\dot{I_C}\)\(=\cfrac{\dot{E}}{X_L}+\cfrac{\dot{E}}{X_C}\)
\(\dot{I_X}=\dot{E}\left(\cfrac{1}{X_L}+\cfrac{1}{X_C}\right)\) [A]
また、\(I_X\) の大きさは
\(I_X=I_C-I_L=E\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)\) [A] となります。
全電流 \(\dot{I}\) は \(\dot{I_R}\) と \(\dot{I_X}\) の合成になります。
\(\dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}\) [A]
全電流 \(I\) の大きさは、三平方の定理から
\(I=\sqrt{{I_R}^2+{I_X}^2}=\sqrt{{I_R}^2+(I_L-I_C)^2}\)
\(I=\sqrt{\left(\cfrac{E}{R}\right)^2+\left(\cfrac{E}{ωL}-ωCE\right)^2}\)
\(I=E\sqrt{\left(\cfrac{1}{R}\right)^2+\left(\cfrac{1}{ωL}-ωC\right)^2}\) [A]
■ \(X_L<X_C\) のときの合成インピーダンス
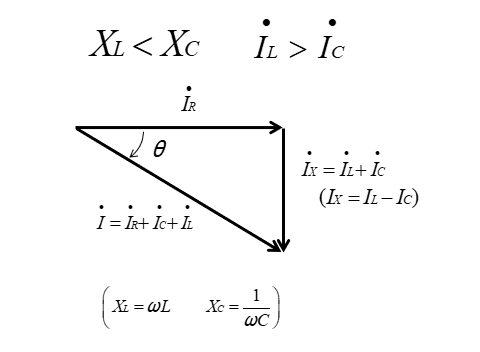
合成インピーダンス \(Z\) は
\(I=E\sqrt{\left(\cfrac{1}{R}\right)^2+\left(\cfrac{1}{ωL}-ωC\right)^2}\) [A] の式より
\(Z=\cfrac{E}{I}\)
\(Z=\cfrac{1}{\sqrt{\left(\cfrac{1}{R}\right)^2+\left(\cfrac{1}{ωL}-ωC\right)^2}}\) [Ω] になります。
■ \(X_L>X_C\) のときのインピーダンス角 θ
インピーダンス角 θ の大きさは
\(θ=\tan^{-1}\cfrac{\cfrac{1}{X_L}-\cfrac{1}{X_C}}{\cfrac{1}{R}}\)
\(θ=\tan^{-1}R\left(\cfrac{1}{ωL}-ωC\right)\) [rad]
■ 極座標表示

\(\dot{I_R}=\cfrac{\dot{E}}{R}\angle 0\) [A] (電圧 \(\dot{E}\) と同相)
\(\dot{I_L}=\cfrac{\dot{E}}{X_L}\angle -\cfrac{π}{2}\) [A] (電圧 \(\dot{E}\) より \(\cfrac{π}{2}\) 遅れ)
\(\dot{I_C}=\cfrac{\dot{E}}{X_C}\angle \cfrac{π}{2}\) [A] (電圧 \(\dot{E}\) より \(\cfrac{π}{2}\) 進み)
\(\dot{I}\angle-θ(シータ)\) [V]
RLC並列回路の記号法による表示
RLC並列回路を記号法で描くと次のようになります。
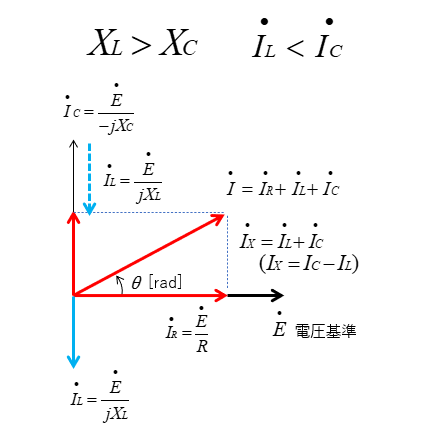
■ \(X_L>X_C\) のときのベクトル図
■ \(X_L<X_C\) のときのベクトル図

■ 虚数単位 \(j\) を付ける場所
- 虚数単位がややこしくなるのは、どこに付けたらいいかわからない。
- \(+j、-j\) どっちになるかわからない。ということではないでしょうか
■ 虚数単位 \(j\) は、\(ω\)(オメガ)の前に \(+j\) を付けると覚えましょう。
これを覚えれば、かなりの部分が解決すると思います。
- \(+j\) は反時計方向に90°移動します。
- \(-j\) は時計方向に90°移動します。
たとえば、容量性リアクタンス \(\cfrac{1}{ωC}=X_C\) の \(ω\) の前に \(j\) を付けます。
\(\cfrac{1}{jωC}=\cfrac{1}{j}×X_C=\cfrac{j}{j}×\cfrac{1}{j}×X_C=-jX_C\) であることがわかります。
記号法によるRLC並列回路の各値の表示

RLC並列回路の各値を記号法により、表示すると次のようになります。
\(\dot{I_R}=\cfrac{\dot{E}}{R}\)
\(\dot{I_L}=-j\cfrac{\dot{E}}{X_L}\)\(=\cfrac{\dot{E}}{jX_L}=\cfrac{\dot{E}}{jωL}\)
\(\dot{I_C}=j\cfrac{\dot{E}}{X_C}\)\(=\cfrac{\dot{E}}{-jX_C}=jωCE\)
回路の全電流 \(\dot{I}\) は、各枝路を流れる電流の和になります。
\(\dot{I}=\cfrac{\dot{E}}{R}+\cfrac{\dot{E}}{jX_L}+\cfrac{\dot{E}}{-jX_C}\)
\(\dot{I}=\left\{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)\right\}\dot{E}\)
\(I=\left\{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{ωL}-ωC\right)\right\}\dot{E}\) [A]
回路の全電流 \(\dot{I}\) は
\(X_L>X_C\) の場合、(\(I_L<I_C\)) ですから進みます。
\(X_L<X_C\) の場合、(\(I_L>I_C\)) ですから遅れます。
電圧 \(\dot{E}\) は
\(\dot{E}=\cfrac{\dot{I}}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)}\)
\(\dot{E}=\cfrac{\dot{I}}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{ωL}-ωC\right)}\) [V] になります。
■ 合成インピーダンスの値
\(\dot{Z}=\cfrac{\dot{E}}{\dot{I}}\) から
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}}\)
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)}\)
ここで、\(\cfrac{1}{X_L}-\cfrac{1}{X_C}=\cfrac{1}{X}\) とすると
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{jX}}\)
\(\dot{Z}=\cfrac{1}{\cfrac{R+jX}{jXR}}\)
\(\dot{Z}=\cfrac{jXR}{R+jX}\)
分母を有理化すると、次のようになります。
\(\dot{Z}=\cfrac{jXR}{R+jX}×\cfrac{R-jX}{R-jX}\)
\(\dot{Z}=\cfrac{R^2jX+X^2R}{R^2+X^2}\)
\(\dot{Z}=\cfrac{X^2R}{R^2+X^2}+j\cfrac{R^2X}{R^2+X^2}\)
インピーダンス \(Z\) の大きさは、次のようになります。
\(Z=\sqrt{\left(\cfrac{X^2R}{R^2+X^2}\right)^2+\left(\cfrac{R^2X}{R^2+X^2}\right)^2}\)
\(Z=\sqrt{\cfrac{R^2X^2(R^2+X^2)}{(R^2+X^2)^2}}\)
\(Z=\cfrac{RX}{\sqrt{R^2+X^2}}\)
■ 記号法による計算
記号法で計算する場合は、誘導性、容量性のどちらのリアクタンスが大きくても、計算式は同じになります。
誘導性リアクタンスと容量性リアクタンスが等しいとき
\(X_L=X_C\) のときは \(I_L\) と \(I_C\) が打ち消し合って、リアクタンスの成分はゼロになります。
コイルとコンデンサが並列接続で共振状態のとき、インピーダンスは無限大になるので接続が切れた状態になります。
RLC並列回路の共振状態では、抵抗だけの回路と同じになります。

■ \(X_L\) と \(X_C\) が共振状態ではなぜインピーダンスが無限大
コイルとコンデンサが並列になっている回路のインピーダンス \(Z\) は
\(Z=\cfrac{1}{jωC+\cfrac{1}{jωL}}\)\(=\cfrac{1}{jωC-j\cfrac{1}{ωL}}\cdots(1)\)
共振状態では \(jωC=j\cfrac{1}{ωL}\) なので式(1)の分母がゼロになります。
\(Z=\cfrac{1}{0}=∞\) になります。
共振回路については、次の記事が参考になります。
RLC並列共振回路
RLC並列回路の公式
■ RLC並列回路の公式
ベクトル
\(X_L=ωL\) [Ω]
\(X_C=\cfrac{1}{ωC}\) [Ω]
\(\dot{I_R}=\cfrac{\dot{E}}{R}\)
\(\dot{I_L}=\cfrac{\dot{E}}{X_L}\)
\(\dot{I_C}=\cfrac{\dot{E}}{X_C}\)
\(\dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}\) [A]
\(\dot{I_X}=\dot{E}\left(\cfrac{1}{X_C}+\cfrac{1}{X_L}\right)\) [A]
記号法
\(\dot{I_L}=-j\cfrac{\dot{E}}{X_L}\)\(=\cfrac{\dot{E}}{jX_L}=\cfrac{\dot{E}}{jωL}\)
\(\dot{I_C}=j\cfrac{\dot{E}}{X_C}\)\(=\cfrac{\dot{E}}{-jX_C}=jωCE\)
\(\dot{I}=\cfrac{\dot{E}}{R}+\cfrac{\dot{E}}{jX_L}+\cfrac{\dot{E}}{-jX_C}\)
\(\dot{I}=\left\{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)\right\}\dot{E}\)
\(\dot{E}=\cfrac{\dot{I}}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)}\)
\(\dot{E}=\cfrac{\dot{I}}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{ωL}-ωC\right)}\) [V]
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}}\)
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{j}\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)}\)
大きさ
\(I_R=\cfrac{E}{R}\) [A]
\(I_L=\cfrac{E}{X_L}=\cfrac{E}{ωL}\) [A]
\(I_C=\cfrac{E}{X_C}=\cfrac{E}{\cfrac{1}{ωC}}=ωCE\) [A]
\(I_X=I_C-I_L=E\left(\cfrac{1}{X_C}-\cfrac{1}{X_L}\right)\) [A]
\(I=\sqrt{{I_R}^2+{I_X}^2}=\sqrt{{I_R}^2+(I_C-I_L)^2}\)
\(I=E\sqrt{\left(\cfrac{1}{R}\right)^2+\left(ωC-\cfrac{1}{ωL}\right)^2}\) [A]
\(Z=\cfrac{1}{\sqrt{\left(\cfrac{1}{R}\right)^2+\left(ωC-\cfrac{1}{ωL}\right)^2}}\) [Ω]
\(θ=\tan^{-1}R\left(ωC-\cfrac{1}{ωL}\right)\) [rad]
練習問題
問題1
抵抗 \(R=10\) [Ω]、誘導リアクタンス \(X_L=2\) [Ω]、容量リアクタンス \(X_C=5\) [Ω] の並列回路の合成インピーダンス \(\dot{Z}\) を求めよ。
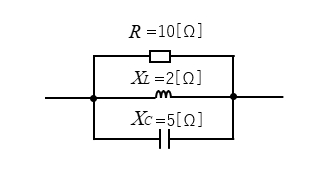
<解答例>
合成インピーダンス \(\dot{Z}\) は次の式から求められます。
\(\dot{Z}=\cfrac{1}{\cfrac{1}{R}+\cfrac{1}{jX_L}+\cfrac{1}{-jX_C}}\)
\(\dot{Z}=\cfrac{1}{\cfrac{1}{10}+\cfrac{1}{j2}+\cfrac{1}{-j5}}\)
\(\quad=\cfrac{1}{0.1-j0.5+j0.2}\)
\(\quad=\cfrac{1}{0.1-j0.3}\)
\(\quad=\cfrac{0.1+j0.3}{0.1^2+0.3^2}\)
\(\quad=\cfrac{0.1+j0.3}{0.1}\)
\(\dot{Z}=1+j3\) [Ω]
\(Z\) の大きさは
\(Z=\sqrt{1^2+3^2}=\sqrt{10}\) [Ω] になります。
問題2
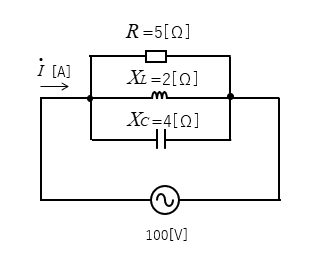
図のような、RLC並列回路に流れる電流 \(I\) を求めよ。
<解答例>
RLC並列回路の電流の大きさは、次の式から求められます。
\(I=E\sqrt{\left(\cfrac{1}{R}\right)^2+\left(\cfrac{1}{X_L}-\cfrac{1}{X_C}\right)^2}\)
\(\quad=100\sqrt{\left(\cfrac{1}{5}\right)^2+\left(\cfrac{1}{2}-\cfrac{1}{4}\right)^2}\)
\(\quad=\sqrt{0.2^2+(0.5-0.25)^2}\)
\(\quad=\sqrt{0.04+0.0625}\)
\(\quad=\sqrt{0.1025}\)
\(I≒32\) [A]
以上で「RLC並列回路の説明」の説明を終わります。