並列回路の特徴は、抵抗にかかる電圧が同じこと。電流はそれぞれの抵抗に分流することです。
抵抗の並列回路
並列回路とは、抵抗を並列接続した回路のことです。
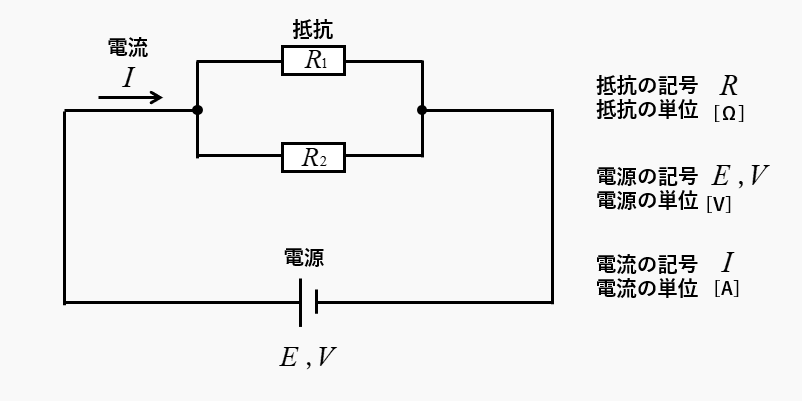
抵抗
抵抗の記号は \(R\) 、単位は [Ω]（オーム）
電圧
電圧の記号は \(E、V\) 、単位は [V]（ボルト）
電流
電流の記号は \(I\) 、単位は [A]（アンペア）
抵抗の並列回路の電圧は同じ大きさになる
並列回路の抵抗の大きさが違っても、抵抗には同じ大きさの電圧がかかります。抵抗の数が2個以上でも、同じ大きさの電圧がかかることは変わりません。
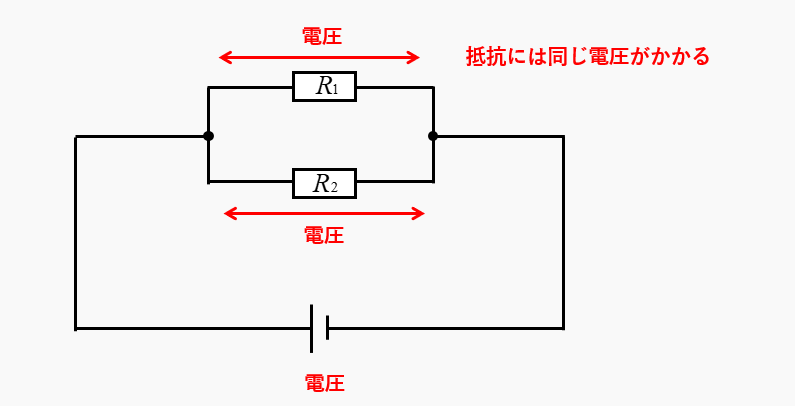
並列回路では、同じ電圧がかかるということが重要なことです。
たとえば、抵抗の代わりに2個の同じ電球を、3Vの電池につなぎます。電球の明るさはどうなるでしょうか？
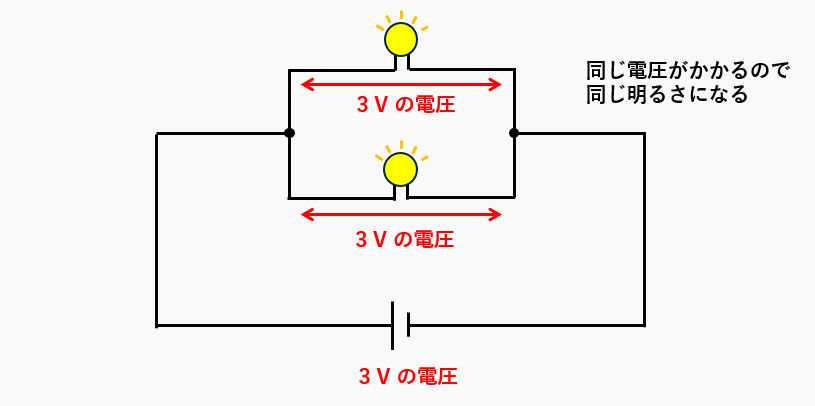
- 並列回路なので、電球には同じ3Vの電圧がかかります。
- したがって、2個の電球の明るさは同じになります。
電球を抵抗とした場合の回路図は、次のようになります。
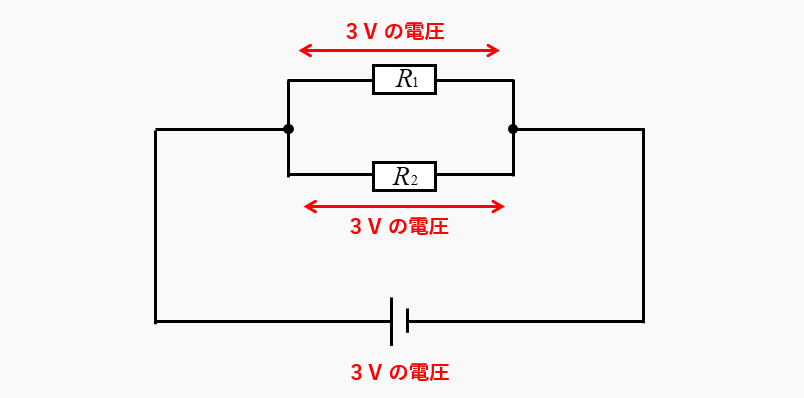
並列回路の電流は分かれて流れる
並列回路に流れる電流は、それぞれの抵抗に分かれて流れます。このことを「電流の分流」といいます。
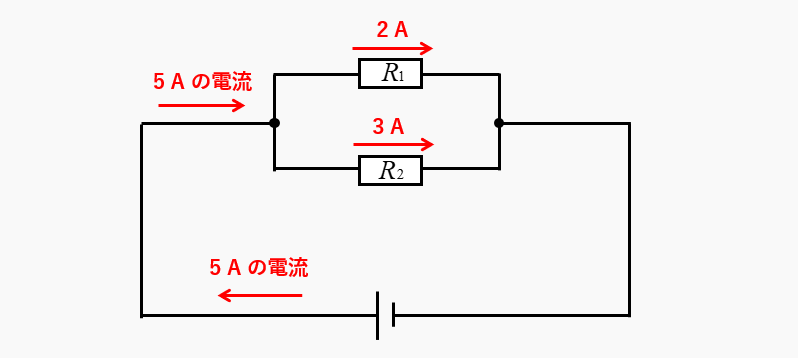
全体の回路に「5A」の電流が流れています。\(R_1\) の抵抗に「2A」の電流が流れている場合、\(R_2\) の抵抗には何アンペアの電流が流れるでしょうか？
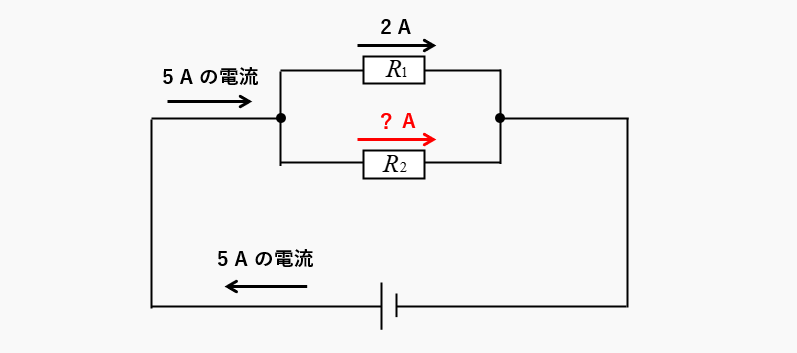
全体を流れる電流「5A」が、2個の抵抗に分かれて流れます。つまり、2個の抵抗に流れる電流を足したものが、全体の電流になります。
全体の電流「5A」は、\(R_1\) の抵抗の電流「2A」と \(R_2\) の抵抗の電流「？A」ですから、5Aから2Aを引いた「3A」が \(R_2\) の抵抗に流れる電流になります。
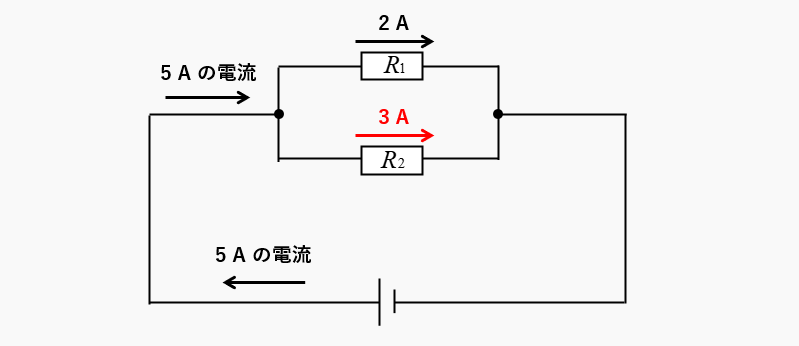
抵抗の並列回路では、それぞれの抵抗に電流が分かれる「分流の法則」があります。
並列回路の抵抗の求め方
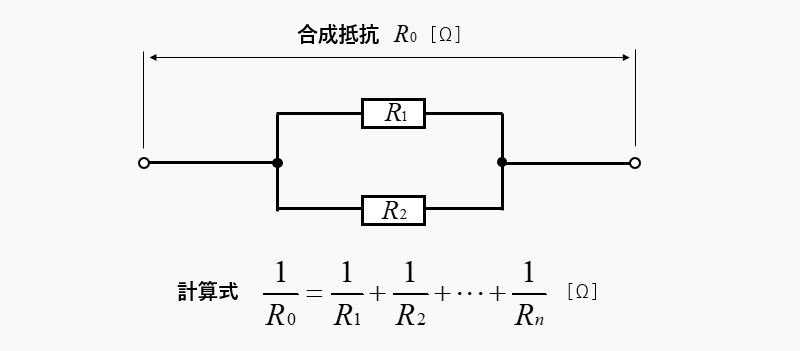
並列回路の、全体の抵抗のことを「合成抵抗」といいます。
並列回路の合成抵抗の逆数は、それぞれの抵抗の逆数の和に等しい。
という法則があります。（合成抵抗＝全体の抵抗）
\(\cfrac{1}{\bf合成抵抗}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\)
例えば、20Ω と 30Ω の抵抗が並列になっているとき、全体の抵抗＝合成抵抗はいくらか？
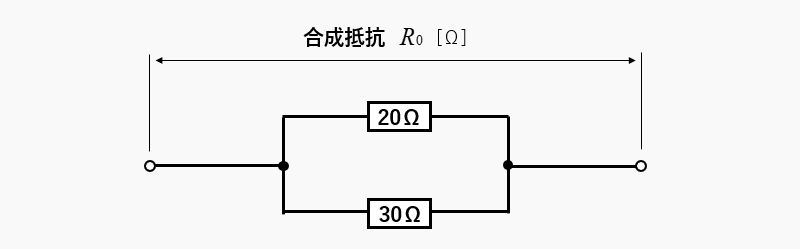
並列回路の公式
\(\cfrac{1}{\bf合成抵抗}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\)
合成抵抗の公式に数値を当てはめると
\(\cfrac{1}{\bf合成抵抗}=\cfrac{1}{20}+\cfrac{1}{30}\)
\(\cfrac{1}{\bf合成抵抗}=\cfrac{5}{60}=\cfrac{1}{12}\)
逆数を直すと合成抵抗は
合成抵抗＝12Ω（オーム）になります。
合成抵抗については、次の記事を御覧ください。
電圧と電流と抵抗の関係
電圧と電流と抵抗の間には、電気回路の重要な法則があります。それは、「オームの法則」です。
オームの法則は、次のようなものです。
- 電圧 V ＝ 抵抗 R × 電流 I
- 抵抗 R ＝ 電圧 V ÷ 電流 I
- 電流 I ＝ 電圧 V ÷ 抵抗 R
オームの法則については、次の記事を御覧ください。
まとめ
並列回路の電圧・電流・抵抗の関係は、次のようになります。
電圧
並列回路の抵抗の大きさが違っても、抵抗には同じ大きさの電圧がかかります。抵抗の数が2個以上でも、同じ大きさの電圧がかかることは変わりません。
電流
並列回路に流れる電流は、それぞれの抵抗に分かれて流れます。このことを「電流の分流」といいます。
抵抗
並列回路の合成抵抗の逆数は、それぞれの抵抗の逆数の和に等しい。
という法則があります。（合成抵抗＝全体の抵抗）
\(\cfrac{1}{\bf合成抵抗}=\cfrac{1}{R_1}+\cfrac{1}{R_2}\)
以上で「【初心者向け】並列回路の電圧・電流・抵抗の関係をわかりやすく解説！」の説明を終わります。