オームの法則とは

オームの法則は、電圧・電流・抵抗の関係を示す 電気回路の重要な法則です、オームの法則の名前は、ドイツの物理学者「ゲオルク・オーム」が由来です。
オームの法則を式で表示すると、電圧 V = 抵抗 R ✕ 電流 I です。
オームの法則の関係を図にすると、次のようになります。
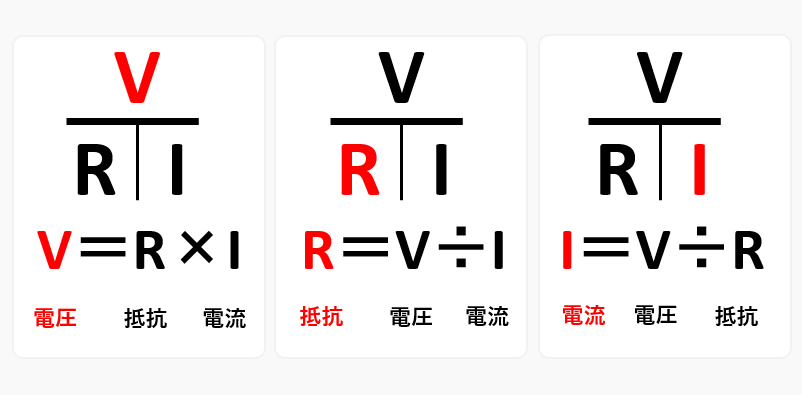
電圧を求めるには、電圧 V = 抵抗 R × 電流 I
抵抗を求めるには、抵抗 R = 電圧 V ÷ 電流 I
電流を求めるには、電流 I = 電圧 V ÷ 抵抗 R
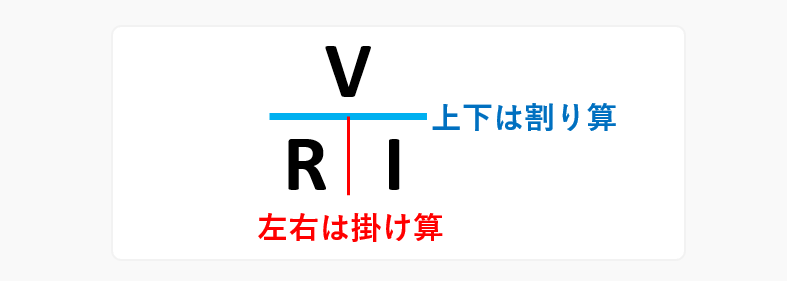
オームの法則の覚え方は、次のように「上下は割り算・左右は掛け算」と覚えましょう。
電圧・電流・抵抗の関係を坂に例えて理解する
初めてオームの法則を見る人のために、電圧・電流・抵抗について簡単に説明します。電圧が1.5Vの時と電圧が3Vの時の、電圧・電流・抵抗の関係を坂に例えると理解しやすくなります。
電圧が1.5Vの時の例
坂の高さを「電圧1.5V」、坂の流れを「電流」、電流の流れを抑える物を「抵抗1.5Ω」とします。
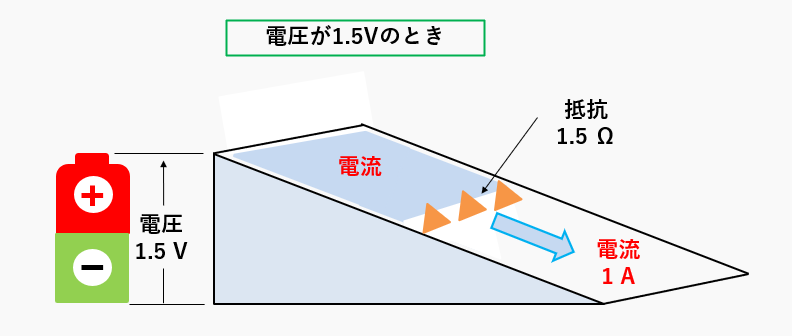
オームの法則により電流は電圧÷抵抗ですから
電流=\(\cfrac{1.5}{1}=1.5\) [A] になります。
電圧が3Vの時の例
上と同様に、坂の高さを「電圧3V」、坂の流れを「電流」、電流の流れを抑える物を「抵抗1.5Ω」とします。
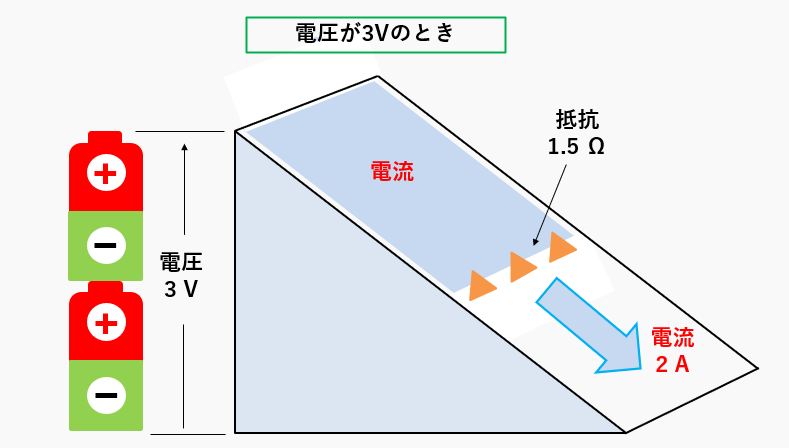
オームの法則により電流は電圧÷抵抗ですから
電流=\(\cfrac{3}{1.5}=2\) [A] になります。
誰にでも、馴染みのある乾電池の電圧は「1.5V」です。乾電池に電球をつなぐと電球が光ります。電球が光るのは、乾電池の持つ電圧が、電球である抵抗を通して、回路に電流が流れるからです。
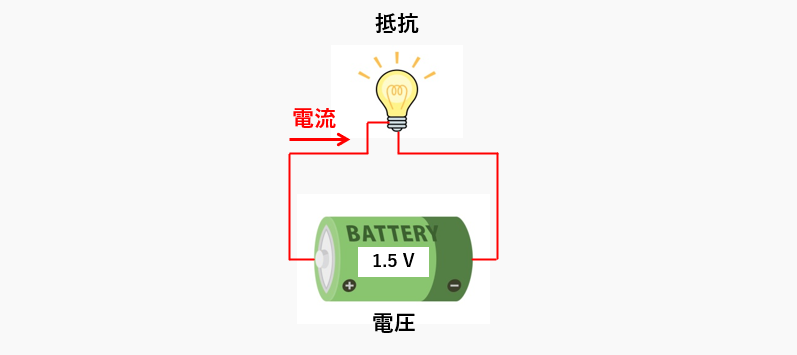
家庭のコンセントの電圧は100Vと、大きいですが電池の場合と、同じように考えることができます。コンセントに来ているのが電圧で、電気製品が抵抗、電気のコードに流れるのが電流です。
つまり、電圧は電気を流す圧力のことで、電流は電気コードに流れるもの、抵抗は電球や電気製品などのことです。
電圧・電流・抵抗の記号や単位、読み方
- 電圧の記号は V で表し、単位は [V ]、単位の読み方は(ボルト)
起電力の場合は、電圧を E で表すことがあります。 - 電流の記号は I で表し、単位は [A]、単位の読み方は(アンペア)
- 抵抗の記号は R で表し、単位は [Ω]、単位の読み方は(オーム)
オームの法則と公式の解説
- 電圧の式 V・・・V = R ✕ I
-
電圧の式から分かるように、電圧 V は、抵抗 R 、電流 I と比例します。
電圧「V」は、抵抗「R」が一定なら電流「I」が増えれば、電圧「V」も大きくなり、電流「I」が減れば電圧「V」も小さくなる。(比例)
- 電流の式 I・・・I = V ÷ R
-
電流の式から分かるように、電流 I は、電圧 V に比例し、抵抗 R に反比例します。
電流「I」は、抵抗「R」が一定なら、電圧「V」が大きくなれば電流「I」が増え、電圧「V」が小さくなれば電流「I」が減ります。(比例)
電流「I」は、電圧「V」が一定なら、抵抗「R」が大きくなれば電流「I」が減り、抵抗「R」が小さくなれば電流「I」が増えます。(反比例)
- 抵抗の式 R・・・R = V ÷ I
-
抵抗の式から分かるように、抵抗 R は、電圧 V に比例し、電流 I に反比例します。
抵抗「R」は、電流が一定なら、電圧「V」が大きくなれば抵抗「R」が大きくなり、電圧「V」が小さくなれば抵抗「R」が小さくなります。(比例)
抵抗「R」は、電圧「V」が一定なら、電流が大きくなれば抵抗「R」が小さくなり、電流が小さくなれば抵抗「R」が大きくなります。(反比例)
オームの法則の使い方
オームの法則は、電圧・電流・抵抗の3つのうち2つが分かれば、残りの数値を知ることができます。
電圧の求め方の例
次の回路で、電圧 V [V] を求めましょう。
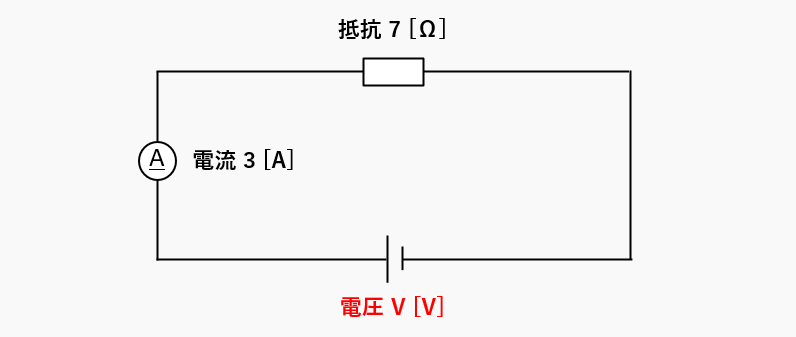
電圧を求める式は・・・電圧 V = 抵抗 R ✕ 電流 I ですから、数値をいれると
7 [Ω] ✕ 3 [A] = 21 [V]
電圧 V は 21 [V] になります。
電流の求め方の例
次の回路で、電流 I [A] を求めましょう。
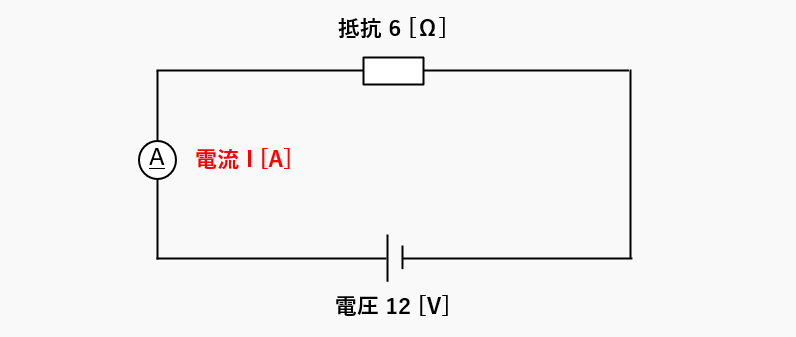
電流を求める式は・・・電流 I = 電圧 V ÷ 抵抗 R ですから、数値をいれると
12 [V] ÷ 6 [Ω] = 2 [A]
電流 I は 2 [A] になります。
抵抗の求め方の例
次の回路で、抵抗 R [Ω] を求めましょう。
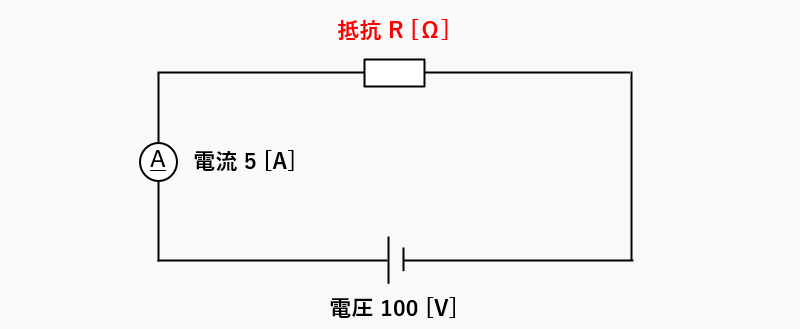
抵抗を求める式は・・・抵抗 R = 電圧 V ÷ 電流 I ですから、数値をいれると
100 [V] ÷ 5 [A] = 20 [Ω]
抵抗 R は 20 [Ω] となります。

オームの法則の複合的な使い方
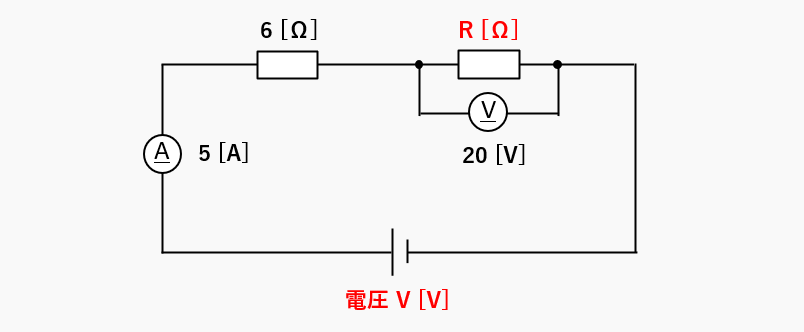
例題1
抵抗の直越回路とオームの法則の問題です。
- 抵抗 R [Ω] の抵抗値
- 電源 V [V] の電圧 を求めましょう。
<解答のポイント>
抵抗の直列回路では、抵抗を流れる電流は同じ大きさです。したがって、抵抗 R には 5 A の電流が流れます。
抵抗を求める式は・・・抵抗 R = 電圧 V ÷ 電流 I ですから、数値をいれると
20 [V] ÷ 5 [A] = 4 [Ω]
抵抗 R は 4 [Ω] となります。
抵抗の直列回路では、回路の電圧がそれぞれの抵抗に分かれます。
6 Ω に掛かる電圧は、電圧の式 V・・・V = R ✕ I から
6 [Ω] ✕ 5 [A] = 30 [V]
6 Ω に掛かる電圧は、30 [V] になります。
電源電圧 V は、「抵抗 R の電圧」と「6 Ω の電圧」を足したものになるので
20 [V]+30 [V]=50 [V]
電源 V [V] の電圧は、50 [V] になります。
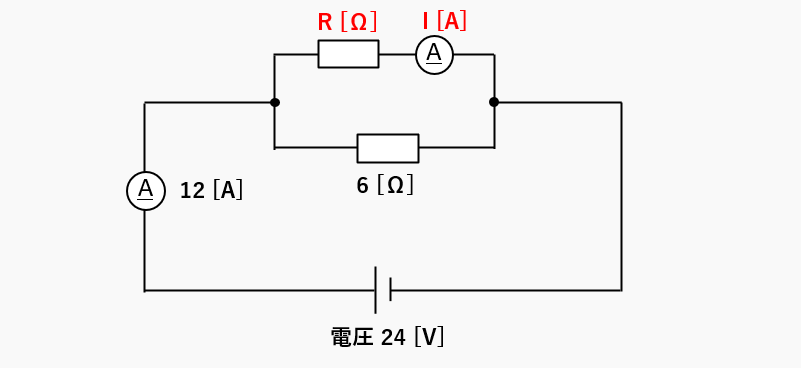
例題2
抵抗の並列回路とオームの法則の問題です。
- 抵抗 R [Ω] の抵抗値
- 電流 I [A] の電流値 を求めましょう。
<解答のポイント>
抵抗の並列回路では、抵抗に掛かる電圧が同じ大きさです。「6 Ω の抵抗」と「R Ω の抵抗」 には 24 V の電圧が掛かります。
6 Ω の抵抗に流れる電流
電流を求める式は・・・電流 I = 電圧 V ÷ 抵抗 R ですから、数値をいれると
24 [V] ÷ 6 [Ω] = 4 [A]
R Ω の抵抗に流れる電流
R Ω に流れる電流は「回路全体の電流」から「6 Ω に流れる電流」を引いたものです。
12 [A] - 4 [A] = 8 [A]
抵抗 R に流れる電流は 8 [A] となります。
R Ω の抵抗の抵抗値
R Ω の抵抗値は、電圧と電流が分かったので、オームの法則から求められます。
24 [V] ÷ 8 [A]=3 [Ω]
抵抗 R の大きさは 3 [Ω] となります。
以上で「初めて見る人が理解できるオームの法則」の説明を終わります。