オームの法則を理解するために、練習問題を集めました。
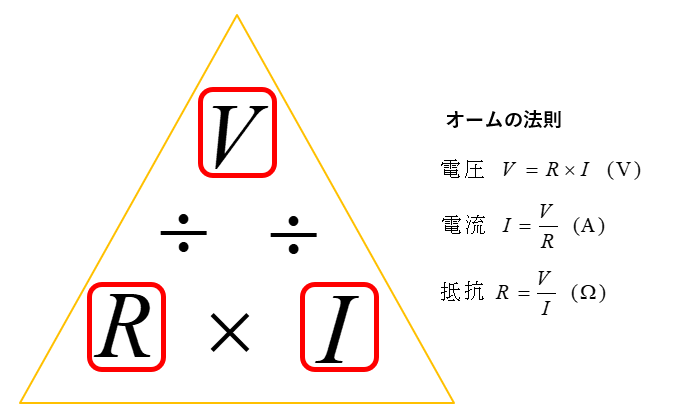
オームの法則
オームの法則は、電気回路の電圧、電流、抵抗の関係を表す法則です。
オームの法則のおさらいです。
\(V=RI\quad\rm[V]\)
\(I=\cfrac{V}{R}\quad\rm[A]\)
\(R=\cfrac{V}{I}\quad\rm[Ω]\)
電圧: \(V\) (ボルト)
電流: \(I\) (アンペア)
抵抗: \(R\) (オーム)
オームの法則の練習問題
問題1
電源電圧 \(E\) [V] を求めよ。
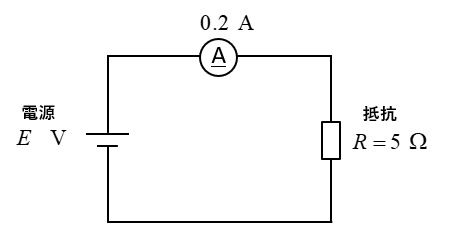
<解答例>
オームの法則 \(E=R×I\) から
\(E=5×0.2=1\) [V]
問題2
抵抗 \(R\) を求めよ。
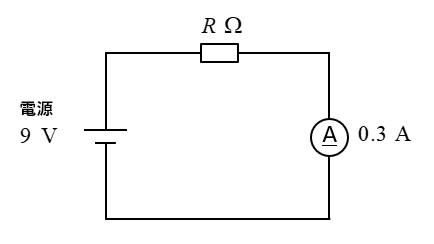
<解答例>
オームの法則 \(R=\cfrac{E}{I}\) から
\(R=\cfrac{9}{0.3}=30\) [Ω]
問題3
電流 \(I\) を求めよ。
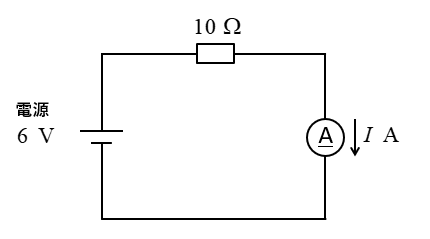
<解答例>
オームの法則 \(I=\cfrac{E}{R}\) から
\(I=\cfrac{6}{10}=0.6\) [A] になります。
問題4
抵抗 \(R\) と電源電圧 \(E\) を求めよ。
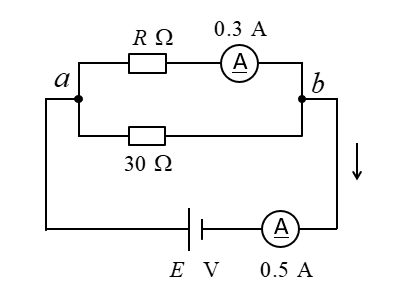
<解答例>
手 順
30Ωに流れる電流を求めて、電源電圧 \(E\) を求めます。
1.全体の電流は、0.5Aなので、30Ωに流れる電流は、0.2Aになります。
2.\(E=30×0.2=6\) [V] になります。
\(R\) の電圧と電流から、抵抗 \(R\) を求めます。
3.Rにかかる電圧は、6V で流れる電流は、0.3A なのでオームの法則から
\(R=\cfrac{6}{0.3}=20\) [Ω] になります。
問題5
抵抗 \(R\) と電源電圧 \(E\) を求めよ。

<解答例>
抵抗 \(R\) に流れる電流は0.4Aなので、オームの法則から
\(R=\cfrac{2}{0.4}=5\) [Ω] になります。
電源電圧 \(E\) はオームの法則から
\(E=(15+5)×0.4=8\) [V] になります。
問題6
抵抗 \(R\) と電流 \(I\) を求めよ。
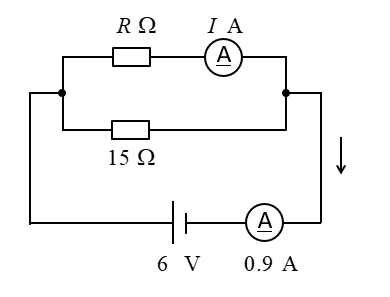
<解答例>
15Ωに流れる電流はオームの法則から
\(\cfrac{6}{15}=0.4\) [A] になります。
\(R\) に流れる電流は
\(I=0.9-0.4=0.5\) [A] になります。
抵抗 \(R\) はオームの法則から
\(R=\cfrac{6}{0.5}=12\) [Ω] になります。
問題7
抵抗 \(R\) と電圧計 \(V\) の値を求めよ

<解答例>
電圧計 \(V\) の値はオームの法則から
\(V=25×0.2=5\) [V] になります。
抵抗 \(R\) にかかる電圧は \(1V\) なので、オームの法則から
\(R=\cfrac{1}{0.2}=5\) [Ω] になります。
問題8
抵抗 \(R\) と電流 \(I\) を求めよ。
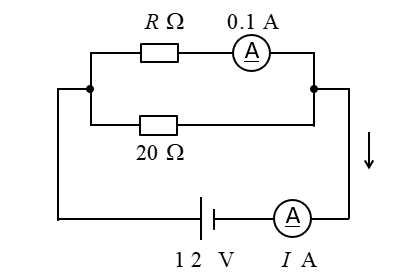
<解答例>
抵抗 \(R\) はオームの法則から
\(R=\cfrac{12}{0.1}=120\) [Ω] になります。
20Ωに流れる電流はオームの法則から
\(\cfrac{12}{20}=0.6\) [A] になります。
回路に流れる電流Iは
\(I=0.1+0.6=0.7\) [A] になります。
問題9
電圧計 \(V\) の値と回路に流れる電流 \(I\) を求めよ。
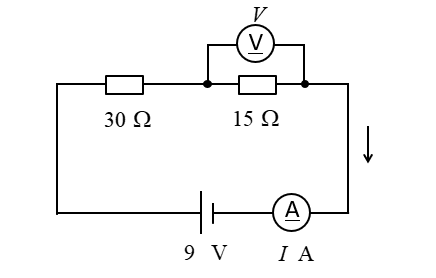
<解答例>
合成抵抗は直列接続なので、\(30+15=45\) [Ω] になります。
回路に流れる電流Iはオームの法則から
\(I=\cfrac{9}{45}=0.2\) [A] になります。
電圧計Vの値はオームの法則から
\(V=15×0.2=3\) [V] になります。
問題10
抵抗 \(R_1\) と \(R_2\) の値を求めよ。
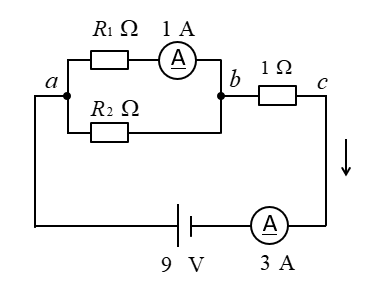
<解答例>
bc間の電圧降下はオームの法則から、\(1Ω×3A=3\) [V] になります
ab感の電圧降下は、\(9V-3V=6\) [V] になります。
抵抗 \(R_1\) はオームの法則から
\(R_1=\cfrac{6}{1}=6\) [Ω] になります。
\(R_2\) に流れる電流は、\(3A-1A=2\) [A] になります。
抵抗 \(R_2\) はオームの法則から
\(R_2=\cfrac{6}{2}=3\) [Ω] になります。
問題11
抵抗 \(R_1\) と回路の合成抵抗 \(R\) を求めよ。
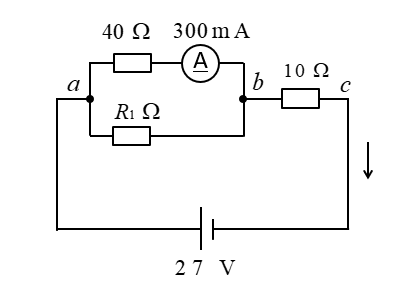
<解答例>
\(300mA=0.3A\) です。
ab間の電圧降下はオームの法則から
\(40Ω×0.3A=12\) [V] になります。
bc間の電圧降下は、\(27V-12V=15\) [V] になります。
10Ωの抵抗に流れる電流はオームの法則から
\(\cfrac{15}{10}=1.5\) [A] になります。
全体の合成抵抗 \(R\) はオームの法則から
\(R=\cfrac{27}{1.5}=18\) [Ω] になります。
抵抗 \(R_1\) に流れる電流は、\(1.5A-0.3A=1.2\) [A] になります。
抵抗 \(R_1\) の値はオームの法則から
\(R_1=\cfrac{12}{1.2}=10\) [Ω] になります。
問題12
抵抗 \(R_1\) と \(R_2\) と電源電圧 \(E\) を求めよ。
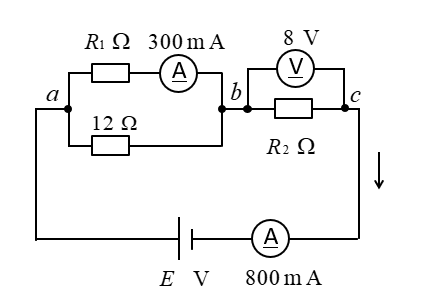
<解答例>
\(300mA=0.3A、800mA=0.8A\) です。
抵抗 \(R_2\) の値はオームの法則から
\(R_2=\cfrac{8}{0.8}=10\) [Ω] になります。
12Ωの抵抗に流れる電流は、\(0.8-0.3=0.5\) [A] になります。
ab間の電圧降下はオームの法則から
\(12Ω×0.5A=6\) [V] になります。
抵抗 \(R_1\) の値はオームの法則から
\(R_1=\cfrac{6}{0.3}=20\) [Ω] になります。
電源の電圧 \(E\) は、\(6+8=14\) [V] になります。
回路の合成抵抗 \(R\) はオームの法則から
\(R=\cfrac{14}{0.8}=17.5\) [Ω] になります。
問題13
電源電圧 \(E\) と合成抵抗 \(R\) を求めよ。
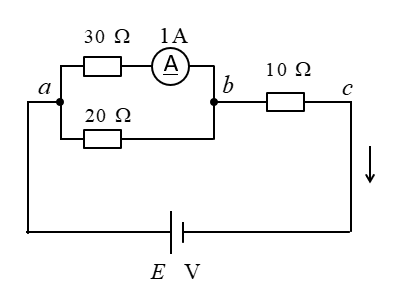
<解答例>
bc間の電圧降下はオームの法則から、\(30Ω×1A=30\) [V] になります。
\(20Ω\) の抵抗に流れる電流はオームの法則から
\(\cfrac{30}{20}=1.5\) [A] になります。
回路全体の電流は \(1A+1.5A=2.5\) [A] になります。
bc間の電圧降下はオームの法則から
\(10Ω×2.5A=25\) [V] になります。
電源電圧は \(E=30V+25V=55\) [V] になります。
全体の合成抵抗 \(R\) はオームの法則から
\(R=\cfrac{55}{2.5}=22\) [Ω] になります。
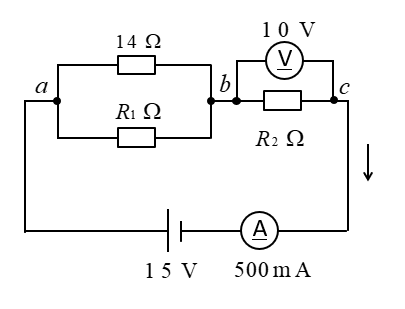
問題14
抵抗 \(R_1\) と抵抗 \(R_2\) の値を求めよ。
<解答例>
\(500mA=0.5A\) です。
ab間の電圧降下は \(15V-10V=5\) [V] になります。
\(14Ω\) の抵抗に流れる電流はオームの法則から
\(\cfrac{5}{14}\) [A] になります。
抵抗 \(R1\) に流れる電流は
\(0.5-\cfrac{5}{14}=\cfrac{1}{7}\) [A] になります。
抵抗 \(R1\) の値はオームの法則から
\(\cfrac{5}{\cfrac{1}{7}}=35\) [Ω] になります。
抵抗 \(R2\) の値はオームの法則から
\(\cfrac{10}{0.5}=20\) [Ω] になります。
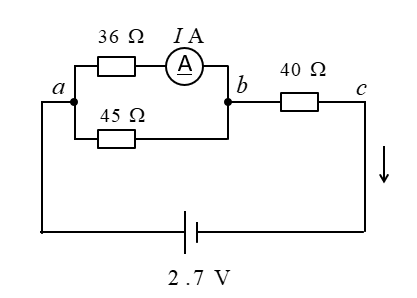
問題15
電流計に流れる電流 \(I\) を求めよ。
<解答例>
ab間の合成抵抗は和分の積より
\(\cfrac{36×45}{36+45}=20\) [Ω] になります。
回路全体の電流はオームの法則から
\(\cfrac{2.7}{60}=0.045\) [A] になります。
>ab間の電圧降下はオームの法則から
\(20Ω × 0.045A=0.9\) [V] になります。
電流計の示す値はオームの法則から
\(\cfrac{0.9}{36}=0.025\) [A] になります。
以上で「オームの法則の問題集」の説明を終わります。