重ね合わせの理とは、2つ以上の複数の電源を持つ回路を解析をする時に有効な定理です。複数の電源を、電源ごとの単独回路に分離することで解析が容易になります。
重ね合わせの理は、電源ごとに分離回路を作り解析します。解析した数値を合わせることで、各枝路の電流値を求めることができます。
同様の解析は、キルヒホッフの法則で計算することができます。
キルヒホッフの法則の場合、回路によっては連立方程式が多くなり計算が面倒になります。
この記事では、重ね合わせの理の解説と具体例を使って説明します。
重ね合わせの理とは?
重ね合わせの理とは、複数の電源を持つ回路の解析をする場合、1つの電源を残した分離回路を作ります。他の電源は短絡して取り除きます。電源の数だけ分離回路を作ります。
分離回路ごとに各枝路の計算をして、計算結果を重ね合わせることで最終的な目的値を求めます。1つの電源の単独回路にすることで、回路の解析が単純化できます。
重ね合わせの理のイメージ
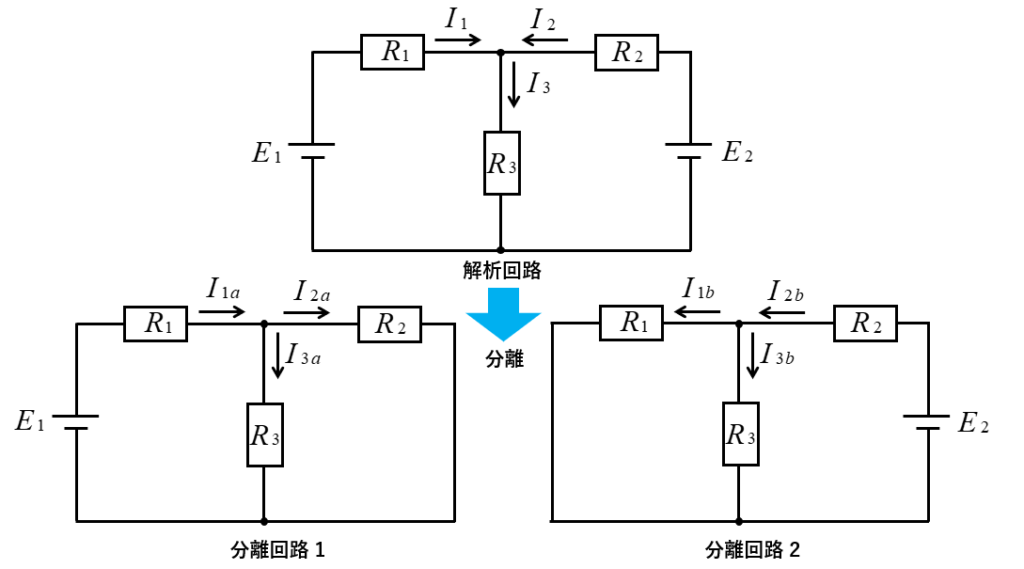
重ね合わせの理は、解析回路を電源ごとに分離回路を作ります。2つの電源なら2つの分離回路を作ります。電源が3つなら分離回路も3つになります。
残した電源以外の電源は、短絡して無いものと考えます。電圧源の場合は「短絡して除去」し、電流源の場合は「開放して除去」します。
重ね合わせの理の手順
- 電源を1つだけ残した回路を、電源の数だけ作ります。
- 電源ごとの回路の計算をします。
- 電源ごとの計算結果を、重ね合わせて目的の数値を求めます。
回路を分離するときに注意すること
- 電源が電圧源の場合・・・電源を「短絡」します。
- 電源が電流源の場合・・・電源を「開放」します。
各枝路の電流のプラスとマイナスの考え方
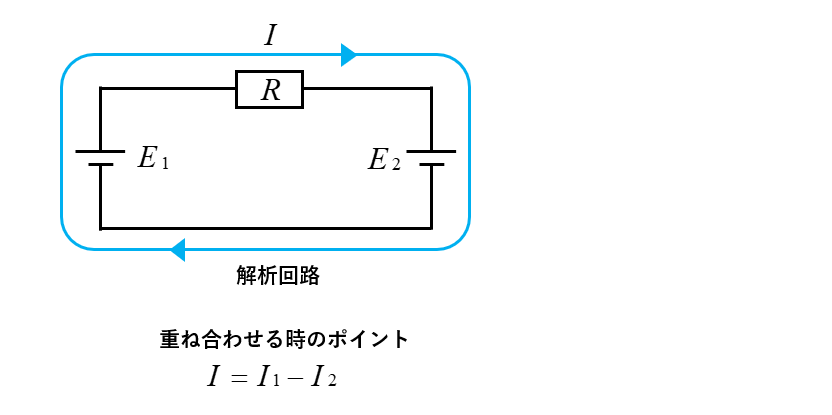
重ね合わせの理を分かりやすくするために、2つの電源と1つの抵抗の回路で説明します。
- 解析回路の電流の向きをプラスとする
-
解析回路の電流 \(I\) の向きを「プラス」として、分離回路の電流の向きを考えます。従って、\(I=I_1+(-I_2)\) になります。

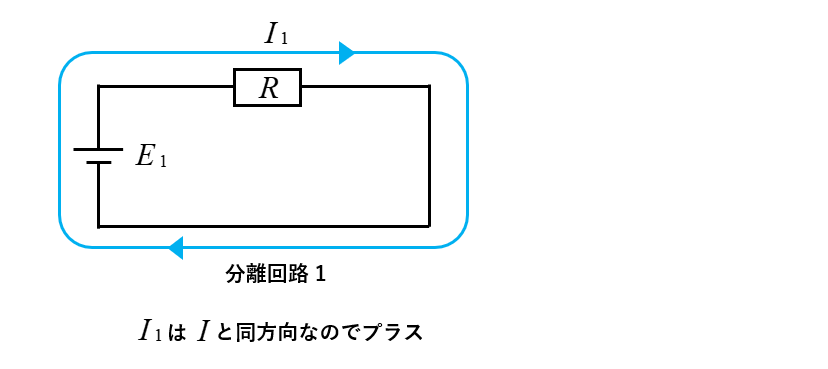
- 分離回路1の電流の向き
-
分離回路 1 の電流 \(I_1\) の向きは、解析回路の電流 \(I\) の向きと同じ方向なので「プラス」になります。

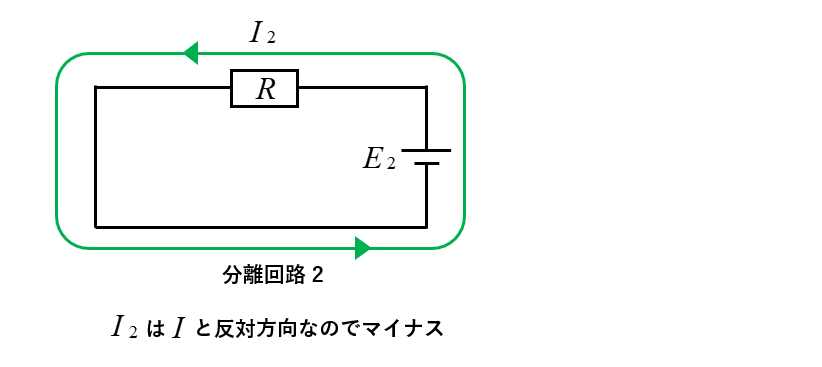
- 分離回路2の電流の向き
-
分離回路 2 の電流 \(I_2\) の向きは、解析回路の電流 \(I\) の向きと反対方向なので「マイナス」です。

重ね合わせの理の使い方の手順と具体例
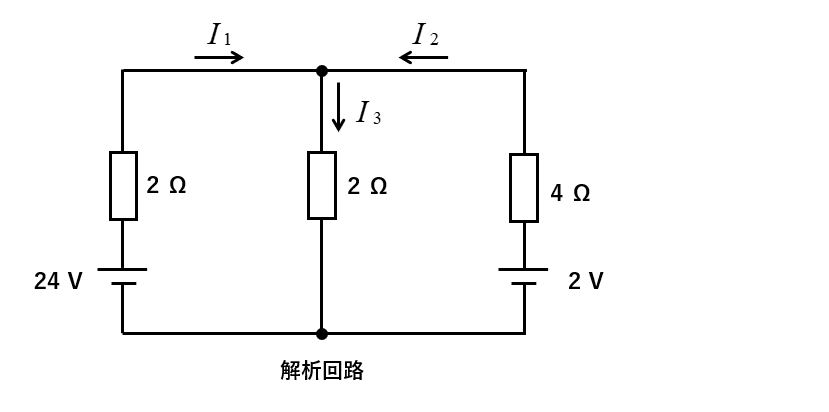
次の図を解析回路の例にして、重ね合わせの理の使い方を説明します。
解析回路の電流の向きを、図のように仮定します。
24Vの電源だけの「分離回路1」の計算
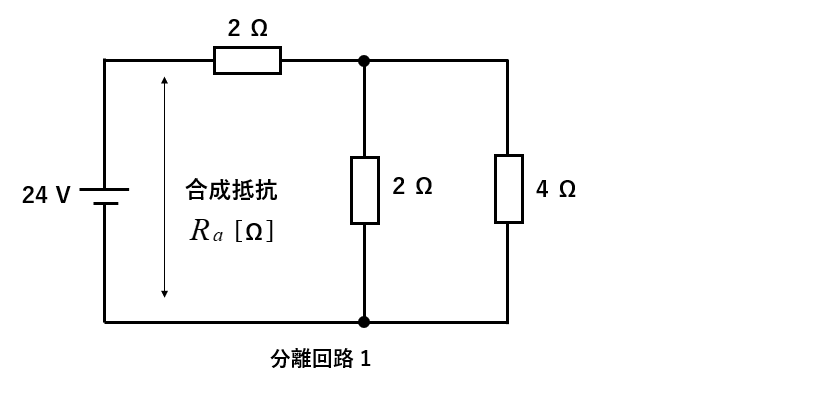
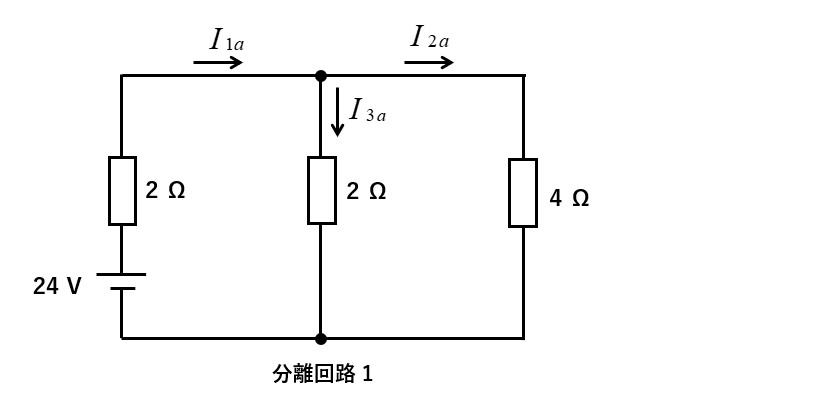
24Vの電源だけを残して、残りの電源を短絡して取り除いた回路を分離回路1とします。
分離回路1の各枝路に流れる、電流の向きと記号を次のように設定します。
電流の向きを電源の方向と合わせると分かりやすくなります。
\(I_{1a}\)、\(I_{2a}\)、\(I_{3a}\)
- 合成抵抗を求めます
-
合成抵抗 \(R_a\) は、直列と並列の合成抵抗です。
\(R_a=2+\cfrac{2×4}{2+4}=\cfrac{10}{3}\) [Ω]

- 枝路電流 \(I_{1a}\) を求めます
-
合成抵抗が求められたので、オームの法則から枝路電流 \(I_{1a}\) が求められます。
\(I_{1a}=\cfrac{24}{\cfrac{10}{3}}=\cfrac{36}{5}\)
- 分流の法則で並列部分の電流を求めます
-
\(I_{2a}=\cfrac{2}{2+4}×\cfrac{36}{5}=\cfrac{12}{5}\)
\(I_{3a}=\cfrac{4}{2+4}×\cfrac{36}{5}=\cfrac{24}{5}\)
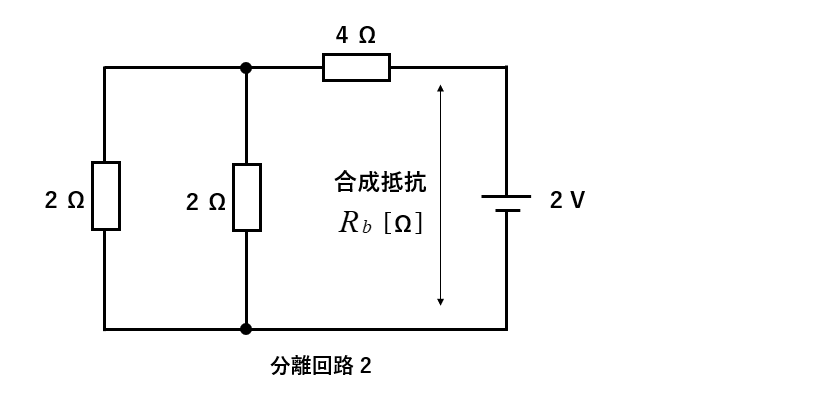
2Vの電源だけの「分離回路2」の計算
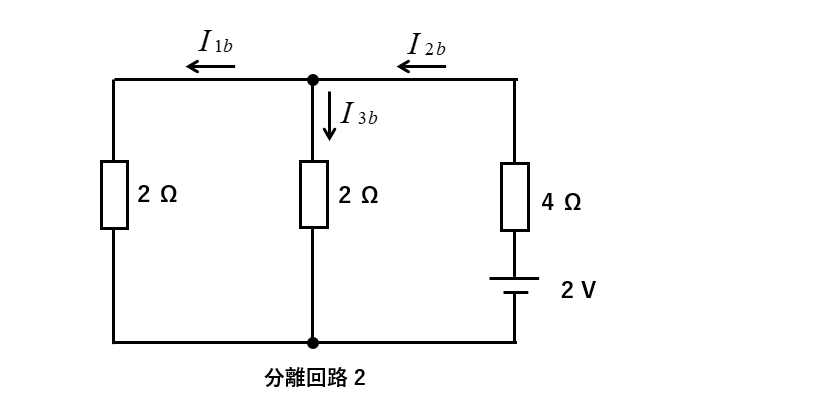
2Vの電源だけを残して、残りの電源を短絡して取り除いた回路を分離回路2とします。
分離回路2の各枝路に流れる、電流の向きと記号を次のように設定します。
\(I_{1b}\)、\(I_{2b}\)、\(I_{3b}\)
- 合成抵抗を求めます
-
合成抵抗 \(R_b\) は、直列と並列の合成抵抗です。
\(R_b=4+\cfrac{2×2}{2+2}=5\) [Ω]

- 枝路電流 \(I_{2b}\) を求めます
-
合成抵抗が求められたので、オームの法則から枝路電流 \(I_{2b}\) が求められます。
\(I_{2b}=\cfrac{2}{5}\)
- 分流の法則で並列部分の電流を求めます
-
\(I_{1b}=\cfrac{2}{2+2}×\cfrac{2}{5}=\cfrac{1}{5}\)
\(I_{3b}=\cfrac{2}{2+2}×\cfrac{2}{5}=\cfrac{1}{5}\)
分離回路1と分離回路2の計算結果から各枝路電流を求める
解析回路において、\(I_1\)、\(I_2\)、\(I_3\) の向きをプラスとしたので、分離回路の電流のプラスマイナスは次のようになります。
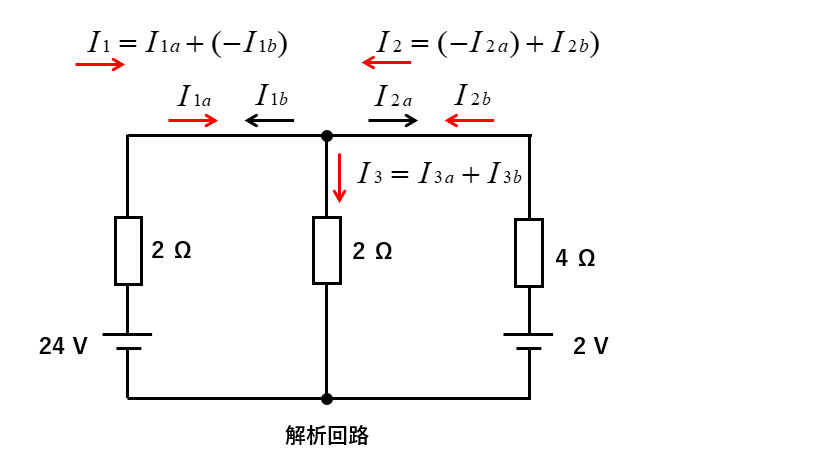
- \(I_{1a}\) は \(I_1\) と同方向で \(I_{1a}=+\cfrac{36}{5}\)
- \(I_{1b}\) は \(I_1\) と反対方向で \(-I_{1b}=-\cfrac{1}{5}\)
- \(I_{2b}\) は \(I_2\) と同方向で \(I_{2b}=+\cfrac{2}{5}\)
- \(I_{2a}\) は \(I_2\) と反対方向で \(-I_{2a}=-\cfrac{12}{5}\)
- \(I_{3a}\) は \(I_3\) と同方向で \(I_{3a}=+\cfrac{24}{5}\)
- \(I_{3b}\) は \(I_3\) と同方向で \(I_{3b}=+\cfrac{1}{5}\)
重ね合わせた各枝路の電流
各枝路の電流は、分離回路1と分離回路2で計算した数値を重ね合わせることで求めます。
\(I_1=I_{1a}+(-I_{1b})=\cfrac{36}{5}-\cfrac{1}{5}=7\) [A]
\(I_2=(-I_{2a})+I_{2b}=-\cfrac{12}{5}+\cfrac{2}{5}=-2\) [A]
\(I_3=I_{3a}+I_{3b}=\cfrac{24}{5}+\cfrac{1}{5}=5\) [A]
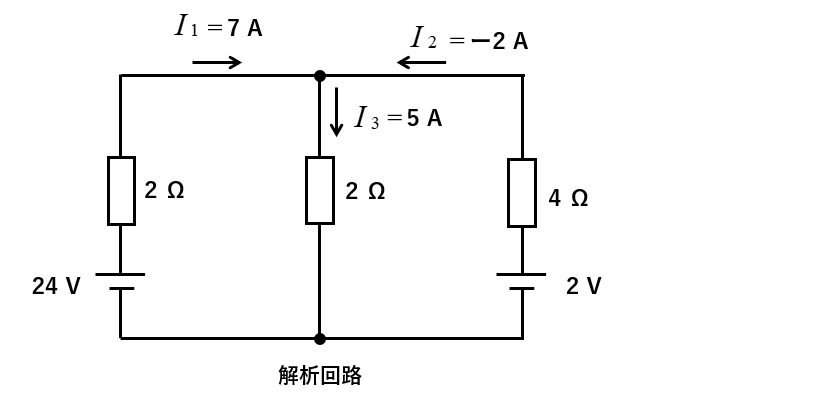
各枝路の電流は、次の図のように流れます。
\(I_2\) の値がマイナスなので、実際に流れる電流の向きは逆方向になります。
重ね合わせの理(電圧源と電流源が混在する場合)
回路に電圧源と電流源が混在する場合
電圧源・・・短絡します。
電圧源の内部抵抗は非常に小さいので短絡する。
電流源・・・開放します。
電流源の内部抵抗は非常に大きいので開放する。
電圧源と電流源の回路の解き方
次の回路には電圧源と電流源があります。
\(3\) [Ω] の抵抗に流れる電流 \(I\) [A] を求めよ。
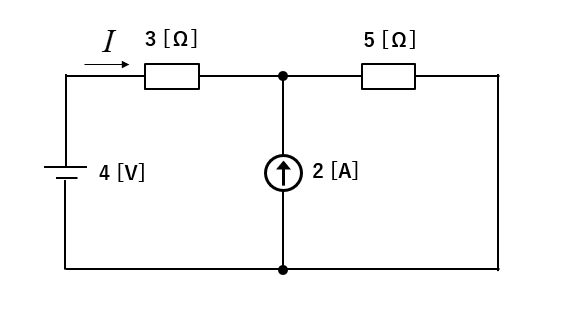
<解答例>
まず、電圧源だけの回路にします。電流源は、開放して取り除きます。
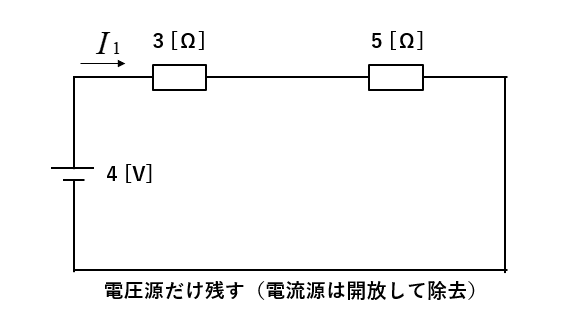
回路に流れる電流を計算する。
\(I_1=\cfrac{4}{3+5}=0.5\) [A]
電流源だけの回路にします。電圧源は短絡します。
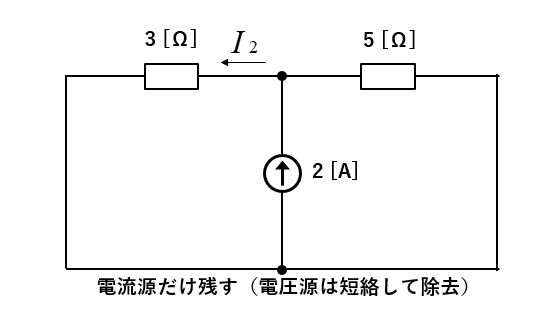
回路に流れる電流を計算する。
\(I_2\) は抵抗が並列接続になっているので、分流の法則 で求めます。
分流の法則については、こちらの記事が参考になります。
\(I_2=2×\cfrac{5}{3+5}=1.25\) [A]
回路に流れる電流 \(I\) は、\(I_1\) と \(I_2\) の和になります。
\(I=I_1+(-I_2)=0.5-1.25=-0.75\) [A] になります。
\(3\) [Ω] の抵抗に流れる電流 \(I_2\) は、\(I_1\) の向きを正方向とすれば
\(I_2\) は逆方向になっているので、\(I=I_1-I_2\) になります。
電流 \(I\) の符号が マイナス なので、向きは左向きになります。

重ね合わせの理のまとめ
重ね合わせの理とは、複数の電源を持つ回路の解析をする場合、1つの電源を残した分離回路を作ります。他の電源は短絡して取り除きます。電源の数だけ分離回路を作ります。
分離回路ごとに各枝路の計算をして、計算結果を重ね合わせることで最終的な目的値を求めます。1つの電源の単独回路にすることで、回路の解析が単純化できます。

重ね合わせの理の手順
- 電源を1つだけ残した回路を、電源の数だけ作ります。
- 電源ごとの回路の計算をします。
- 電源ごとの計算結果を、重ね合わせて目的の数値を求めます。
回路を分離するときに注意すること
- 電源が電圧源の場合・・・電源を「短絡」します。
- 電源が電流源の場合・・・電源を「開放」します。