キルヒホッフの法則は、オームの法則と並び、電気回路の解析において重要な法則です。キルヒホッフの法則は、1845年にグスタフ・キルヒホッフが発見した法則です。
- キルヒホッフの第1法則
-
任意の分岐点において、流入する電流の和は流出する電流の和に等しい。
- キルヒホッフの第2法則
-
任意の閉回路において、起電力の和は電圧降下の和に等しい。
キルヒホッフの第1法則

キルヒホッフの第1法則
任意の分岐点において、流入する電流の和は流出する電流の和に等しい。
分岐点では流れ込む電流と流れ出る電流は等しくなる
キルヒホッフの第1法則は、分岐点Pに流れ込む電流の量と、流れ出る電流の量が等しいということです。
「10アンペアの電流が流れ込んでいれば、出ていく電流も10アンペアの電流が流れ出る」という事を言ってます。
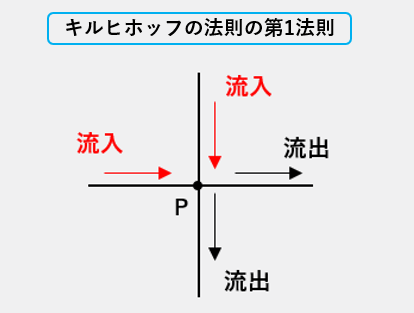
任意の分岐点とは?
任意の分岐点とは、図の赤丸のように、回路のどこでも良いという意味になります。

電流の向きの決め方は自由です
電流の向きは自由に決めて構いませんが、電源から流れる向きに決めるとわかりやすくなります。
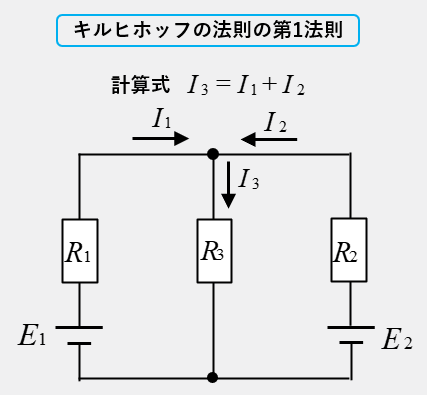
\(I_1\) は電源 \(E_1\) があるので右向きに、\(I_2\) は電源 \(E_2\) があるので左向きにします。
\(I_1\) と \(I_2\) が流れ込む向きなので、\(I_3\) は流れ出る向きにします。

キルヒホッフの第1法則の計算式の例
流入する和と流出する和が等しいので、\(I_1\) と \(I_2\) を流入、\(I_3\) を流出とすれば、\(I_3=I_1+I_2\) となります。
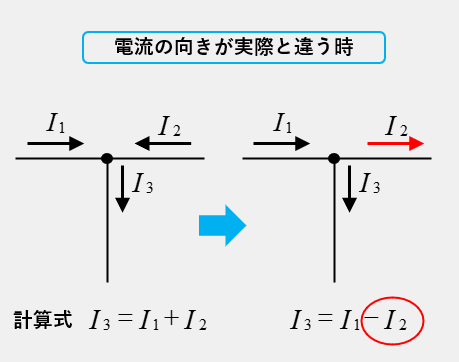
電流の向きが実際の向きと違う時はどうなるの?
もし、計算した結果、電流 \(I_2\) が実際の流れの向きと違う時はどうなるかと言うと、\(I_2\) にマイナスの記号がつきます。
計算結果にマイナスが付いたら、仮定した電流の向きと反対の向きに流れると考えれば良いわけです。
キルヒホッフの第2法則
任意の閉回路において、起電力の和は電圧降下の和に等しい。
キルヒホッフの第2法則では、閉回路の向きを決めて計算式を立てます。どの向きをとっても構いませんが、起電力の向きに閉回路を決めると問題が解きやすくなります。
起電力と電圧降下のプラス・マイナスの決め方
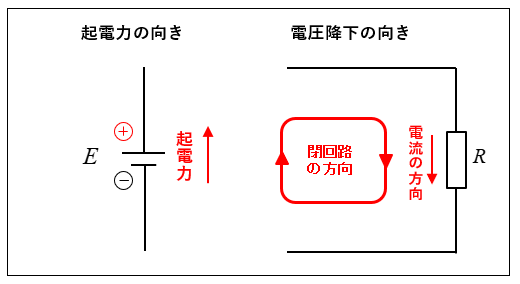
- 起電力のプラス・マイナスの決め方
-
起電力の向きと閉回路の向きが同方向の場合・・・プラス
起電力の向きと閉回路の向きが反対方向の場合・・・マイナス - 電圧降下のプラス・マイナスの決め方
-
電流の向きと閉回路の向きが同方向の場合・・・プラス
電流の向きと閉回路の向きが反対方向の場合・・・マイナス
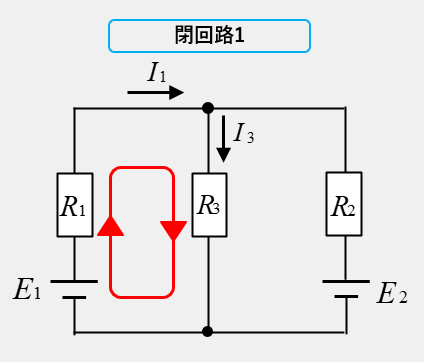
閉回路1の計算方法
閉回路1の向きが右向きの場合、電源 \(E_1\) はプラス、抵抗 \(R_1\) と \(R_3\) の電圧降下がプラスなので
\(E_1=R_1I_1+R_3I_3\) となります。
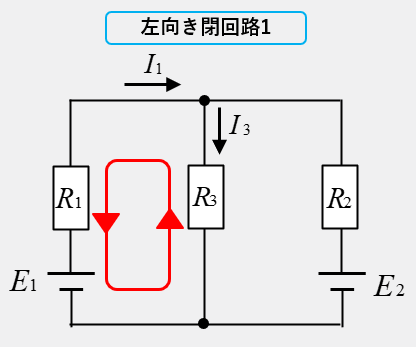
もし、閉回路を左向きと仮定すると、電源 \(E_1\) はマイナス、抵抗 \(R_1\) と \(R_3\) の電圧降下がマイナスなので
\(-E_1=-(R_1I_1+R_3I_3)\) となります。
\(-E_1+R_1I_1+R_3I_3=0\) とすれば、「電位差の和が0」ということになります。
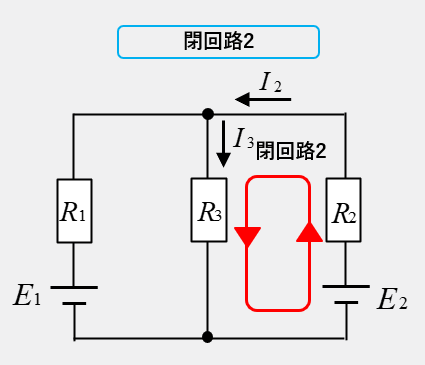
閉回路2の計算方法
閉回路2の向きが左向きの場合、電源 \(E_2\) はプラス、抵抗 \(R_2\) と \(R_3\) の電圧降下はプラスなので
\(E_2=R_2I_2+R_3I_3\) となります。
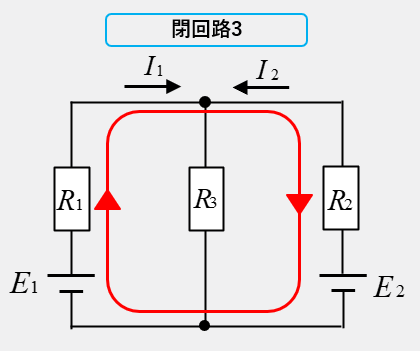
閉回路3の向きが右向きの場合、電源 \(E_1\) はプラス、電源 \(E_2\) はマイナス、抵抗 \(R_1\) の電圧降下はプラス、抵抗 \(R_2\) の電圧降下はマイナスですから
\(E_1-E_2=R_1I_1-R_2I_2\) となります。
3つの閉回路の内の、2つの閉回路と第1法則を使えば問題を解くことができます。
閉回路や電圧降下のプラス・マイナスについては、次の記事をご覧ください。
キルヒホッフの法則で例題を解析する
次の回路において、分岐点をPとして回路に流れる電流をキルヒホッフの法則で求めます。
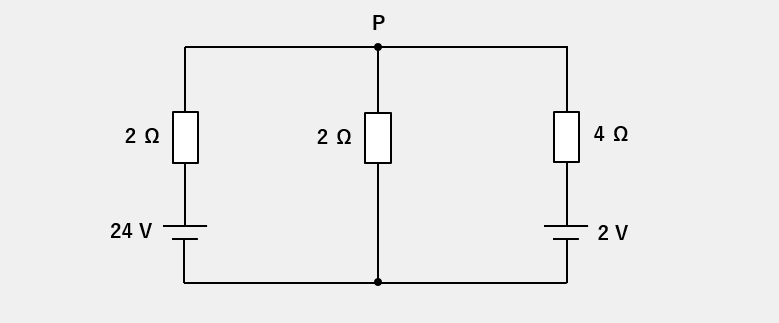
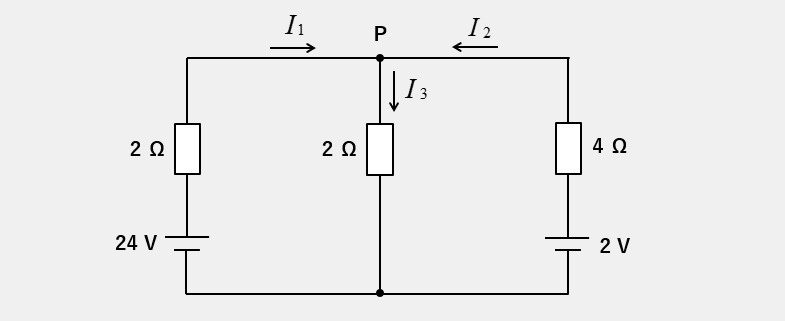
キルヒホッフの第1法則で分岐点の電流関係を表す
分岐点Pの電流の向きを、キルヒホッフの第1法則で次のように仮定します。
\(I_3=I_1+I_2\cdots(1)\)
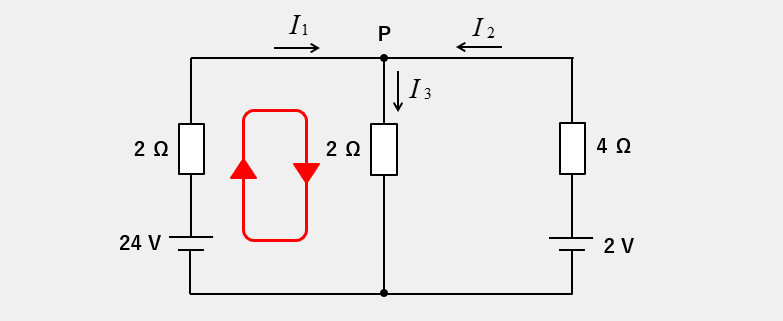
キルヒホッフの第2法則で閉回路1の計算をする
閉回路1をキルヒホッフの第2法則で、右向きに取ります。電源24Vはプラス、2つの抵抗 2Ωの電圧降下はプラスなので
\(24=2I_1+2I_3\cdots(2)\)
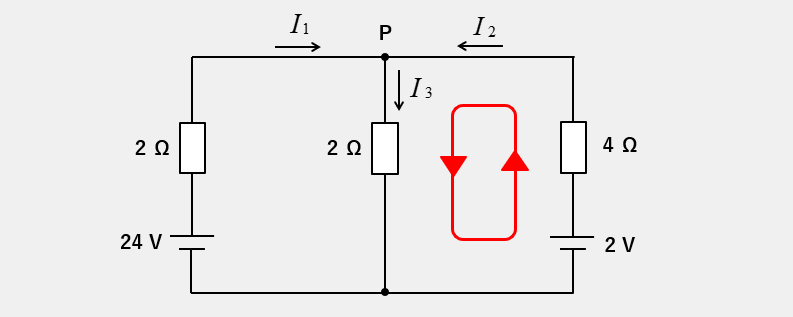
キルヒホッフの第2法則で閉回路2の計算をする
閉回路2をキルヒホッフの第2法則で、左向きに取ります。電源2Vはプラス、抵抗 4Ωと2Ωの電圧降下がプラスなので
\(2=4I_2+2I_3\cdots(3)\)
例題の計算方法
\(I_3=I_1+I_2\cdots(1)\)
\(24=2I_1+2I_3\cdots(2)\)
\(2=4I_2+2I_3\cdots(3)\)
式(1)を式(2)と式(3)に代入すると、式(2)は \(24=4I_1+2I_2\) になり、更に 3倍します。
\(72=12I_1+6I_2\cdots(4)\)
式(3)は \(2=2I_1+6I_2\cdots(5)\)
式(4)から式(5)を引くと、\(70=10I_1\)
\(I_1=7\) [A]
式(5)に \(I_1\) を代入すると
\(I_2=-2\) [A]
式(1)に \(I_1\) と \(I_2\) を代入すると
\(I_3=5\) [A] になります。
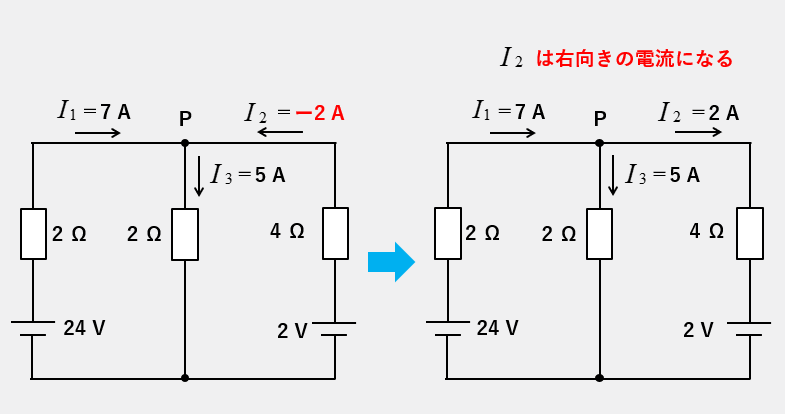
補足
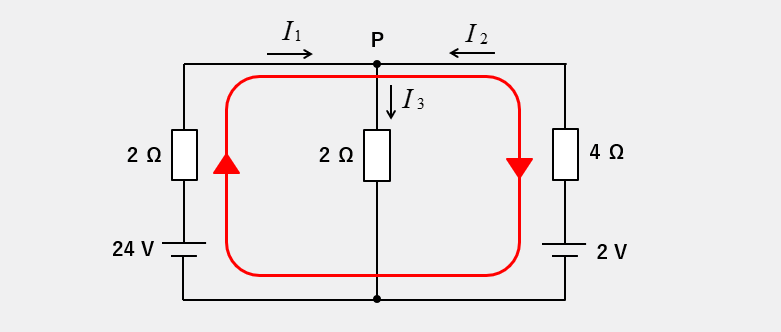
3つ目の閉回路として、次の閉回路を使うこともできます。右向きの閉回路を取ると計算式は、電源の 24V はプラスで 2V はマイナスになり、2Ω の電圧降下はプラスで 4Ω の電圧降下はマイナスになります。
\(22=2I_1-4I_2\) この式を、式(2、3)と組み合わせて計算できます。
まとめ
キルヒホッフの第1法則で、電流の記号と向きを決める。
キルヒホッフの第2法則で、閉回路の向きを決めて、起電力の和=電圧降下の和として計算式を作る。
- キルヒホッフの第1法則
-
任意の分岐点において、流入する電流の和は流出する電流の和に等しい。
- キルヒホッフの第2法則
-
任意の閉回路において、起電力の和は電圧降下の和に等しい。