キルヒホッフの法則を、実際の問題を使って説明します。
キルヒホッフの第1法則は、電流に関する法則です。
電気回路の任意の分岐点において、流入する電流の和は流出する電流の和に等しい。
キルヒホッフの第2法則は、電圧に関する法則です。
電気回路の任意の閉回路におけて、起電力の和と電圧降下の和は等しい。
キルヒホッフの法則の練習問題
問題1
キルヒホッフの法則を使って、各抵抗に流れる電流を求めよ。
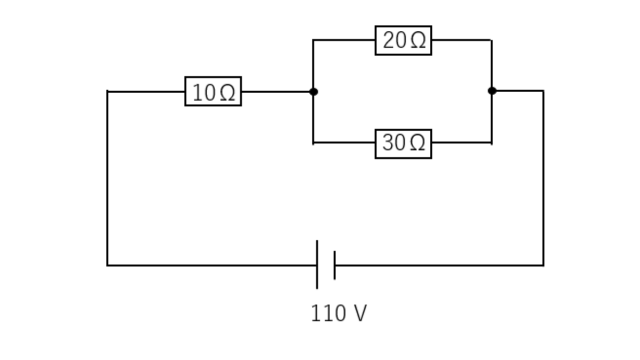
<解答例>
手順1
回路に流れる電流を、図のように決めます。
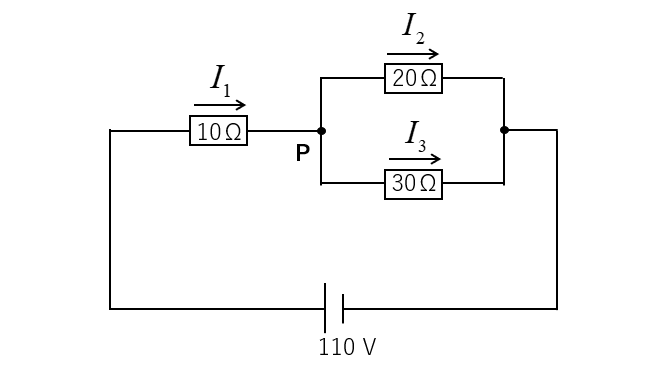
分岐点 P において、キルヒホッフの法則の第1法則を適用すると
\(I_1=I_2+I_3\cdots(1)\)
手順2
閉回路1
次のような、閉回路を取ります。
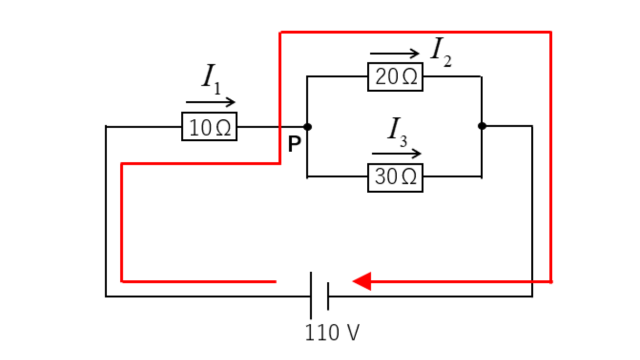
閉回路に、キルヒホッフの第2法則を適用すると
起電力 閉回路の向きと起電力の向きが同じなので「プラス」
電圧降下 10Ωの抵抗と20Ωの抵抗の閉回路の向きと、電流の向きが同じなので「プラス」
起電力の和=電圧降下の和 なので
\(110=10I_1+20I_2\cdots(2)\)
閉回路2
次のような、閉回路を取ります。

閉回路に、キルヒホッフの第2法則を適用すると
起電力 閉回路に起電力が無いので「ゼロ」
電圧降下 20Ωの抵抗の閉回路の向きと、電流の向きが同じなので「プラス」
電圧降下 30Ωの抵抗の閉回路の向きと、電流の向きが同じなので「プラス」
起電力の和=電圧降下の和 なので
\(0=20I_2-30I_3\cdots(3)\)
計算結果
\(I_1=I_2+I_3\cdots(1)\)
\(110=10I_1+20I_2\cdots(2)\)
\(0=20I_2-30I_3\cdots(3)\)
式(1)、式(2)、式(3)を計算すると
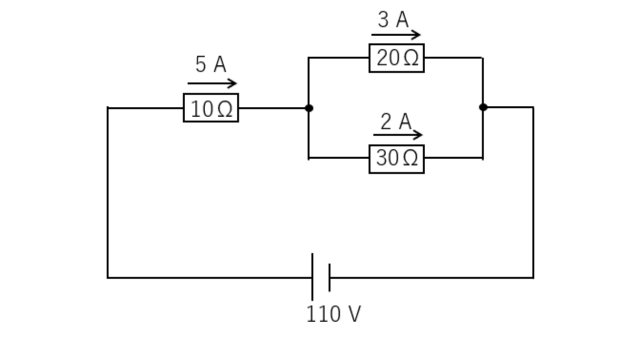
\(I_1=5\) [A]
\(I_2=3\) [A]
\(I_3=2\) [A] になります。
問題2
キルヒホッフの法則で、回路に流れる電流 \(I_1、I_2、I_3\) を求めよ。
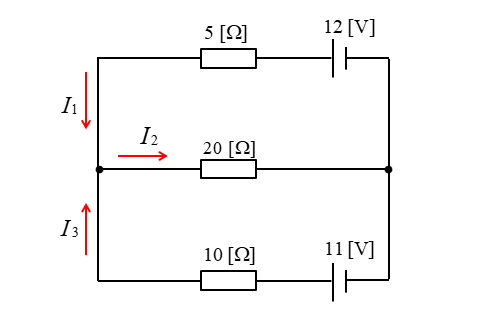
<解答例>
1.分岐点 P における電流の関係は、キルヒホッフの第1法則から
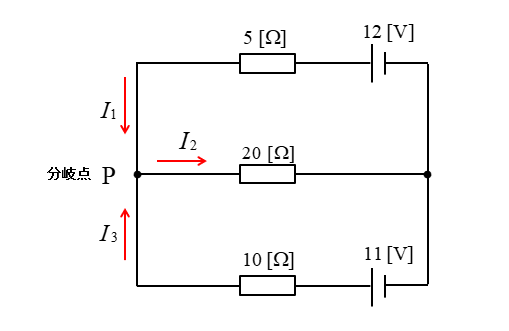
\(I_1-I_2+I_3=0\)
\(I_1+I_3=I_2\cdots(1)\)
2.図の上の回路で矢印の方向に閉回路を考えたとき、キルヒホッフの第2法則から
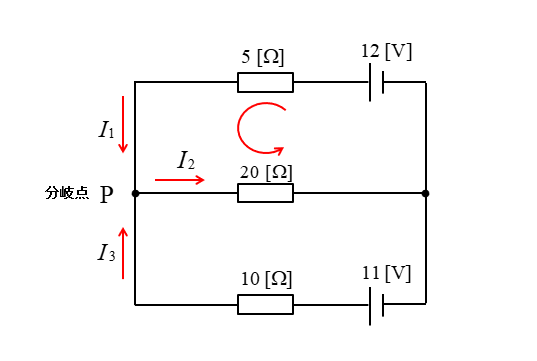
\(5I_1+20I_2=12\cdots(2)\)
3.図の下の回路で矢印の方向に閉回路を考えたとき、キルヒホッフの第2法則から
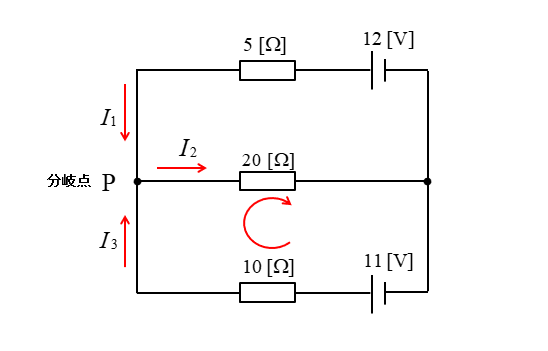
\(I_1+I_3=I_2\cdots(1)\)
\(5I_1+20I_2=12\cdots(2)\)
\(10I_3+20I_2=11\cdots(3)\)
式(1)を式(2)に代入すると
\(5I_1+20(I_1+I_3)=12\)
\(25I_1+20I_3=12\cdots(4)\)
式(3)を変形して、式(2)に代入すると
\(20I_2=11-10I_3\)
\(5I_1+(11-10I_3)=12\)
\(5I_1-10I_3=1\cdots(5)\)
式(5)を変形して、両辺を2倍すると
\(20I_3=10I_1-2\cdots(6)\)
式(6)を式(4)に代入すると
\(25I_1+(10I_1-2)=12\)
\(35I_1=14\)
\(I_1=0.4\) [A]
\(I_1\) を式(6)に代入すると
\(I_3=0.1\) [A]
\(I_2=I_1+I_3\) ですから
\(I_2=0.4+0.1=0.5\) [A] になります。
問題3
次の回路の電流 \(I_1、I_2\) を求めよ。
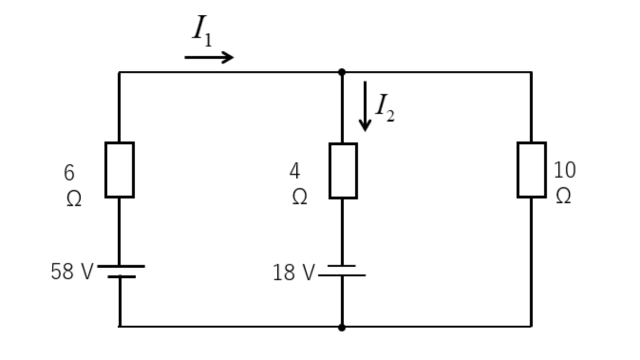
<解答例>
ここではループ電流法を使って、回路を解きます。
\(10\) [Ω] に流れる電流を \(I_1-I_2\) とします。
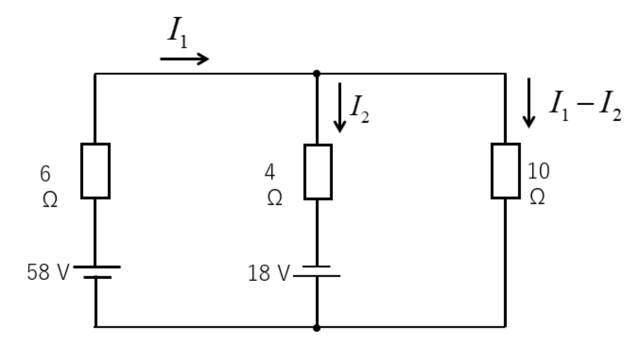
閉回路と向きを決めます。
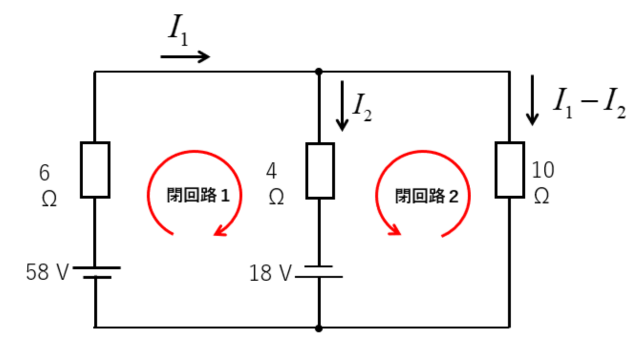
閉回路1で式を立てます。
\(58+18=6I_1+4I_2\)
\(76=6I_1+4I_2\cdots(1)\)
閉回路2で式を立てます。
\(18=4I_2-(I_1-I_2)×10\)
\(18=-10I_1+14I_2\cdots(2)\)
連立方程式を解きます。
式(1)に5を掛けて、式(2)に3を掛けて足し算をします。
\(380=30I_1+20I_2\)
\(54=-30I_1+42I_2\)
2つの式を足し算します。
\(434=62I_2\)
\(I_2=7\) [A]
\(I_2\) を式(2)に代入すると
\(18=-10I_1+14×7\)
\(I_1=8\) [A]
したがって
\(I_1=8\) [A]
\(I_2=7\) [A]
\(10\) [Ω] に流れる電流は次のようになります。
\(I_1-I_2=1\) [A]
以上で「キルヒホッフの法則の練習問題」の説明を終わります。