ミルマンの定理

ミルマンの定理は

複数の電源と抵抗が、並列に接続された回路において

端子電圧を簡単に求めることができる定理のことです。

ミルマンの定理

ミルマンの定理は、複数の電源と抵抗が、並列に接続された回路において

端子電圧　を簡単に求めることができる定理のことです。

ミルマンの定理は　全電圧の定理　または（帆足（ほあし）・ミルマンの定理　ともいわれます。

図のような、回路があったとき

端子電圧を \(V\)、電流を \(I\)、コンダクタンスを \(G\) とすると

\(V=\cfrac{I}{G}\quad\rm[V]\)　で求めることができます。

\(V=\cfrac{I}{G}\)　の式は

\(I=\displaystyle \sum _{ i=1 }^n\cfrac{E_i}{R_i}\)

\(G=\displaystyle \sum_{i=1}^n\cfrac{1}{R_i}\) とすると

\(V= \cfrac{ \displaystyle \sum _{ i=1 }^n\cfrac{E_i}{R_i}}{\displaystyle \sum_{i=1}^n\cfrac{1}{R_i}}\)　になります。

■　∑（シグマ）の意味

たとえば、\(\displaystyle \sum_{i=1}^{4}R_i\)　という式の意味は、次のようなことです。

\(R_i\)　の　\(i\)　に　 1　から　 4　を代入して、合計するということで

\(\displaystyle \sum_{i=1}^{4}R_i=R_1+R_2+R_3+R_4\)　と言う意味になります。

ミルマンの定理の使い方

ミルマンの定理は、図のような複数の電源と複数の抵抗が、並列に接続された回路の端子電圧　\(V\)　を求めるときに使います。

ミルマンの定理を使うには、次の図のように　\(n\)　個の回路に考えます。

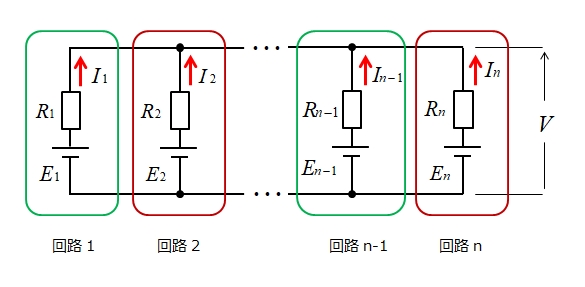
■　各回路のコンダクタンスを求める。

各回路ごとに、コンダクタンスを求めて、それぞれのコンダクタンスを足し算します。

合成コンダクタンス　\(G\)　は

\(G=G_1+G_2\cdots G_{n-1}+G_n\)

\(G=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cdots \cfrac{1}{R_{n-1}}+\cfrac{1}{R_n}\)　となります。

■　各回路の電流を求める。

各回路ごとに、電流を求めて、それぞれの電流を足し算します。

このときに、求めた電流値はミルマンの定理を使うためのもので、実際に回路の枝路に流れる電流値とは異なります。

\(I=I_1+I_2\cdots I_{n-1}+I_n\)
\(I=\cfrac{E_1}{R_1}+\cfrac{E_2}{R_2}+\cdots \cfrac{E_{n-1}}{R_{n-1}}+\cfrac{E_n}{R_n}\)　となります。

■　端子電圧を求める。

端子電圧は、次の式から求められます。

\(V=\cfrac{I}{G}\)＝\(\cfrac{ \displaystyle \sum _{ i=1 }^n\cfrac{E_i}{R_i}}{\displaystyle \sum_{i=1}^n\cfrac{1}{R_i}}\quad\rm[V]\)　

ミルマンの定理の練習問題

わかりやすいように、数値を入れた回路で計算をしてみます。

問題1

ミルマンの定理を使って、回路図の　\(6\)　[Ω]　にかかる電圧　\(V\)　を求めます。

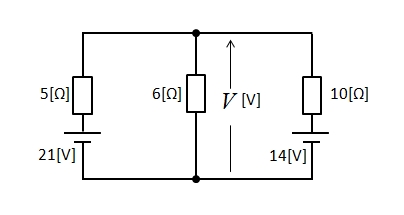
＜解答例＞

ミルマンの定理を使えば、端子電圧　\(V\)　は、次のように求められます。

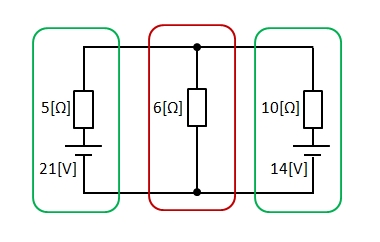
■　合成コンダクタンスを求める。

回路ごとにコンダクタンス　\(G\)　を求めます。

コンダクタンスは並列になっているので、それぞれのコンダクタンスを足し算をすれば良いことになります。

\(G=\cfrac{1}{5}+\cfrac{1}{6}+\cfrac{1}{10}=\cfrac{14}{30}\)　[S]

■　ミルマンの定理の電流を求める。

それぞれの回路について、電流を求めます。

合成電流は、それぞれの電流を足し算します。

\(I=\cfrac{21}{5}+\cfrac{0}{6}+\cfrac{14}{10}=\cfrac{168}{30}\)　[A]

抵抗だけで起電力がないときは、単純に起電力をゼロにすれば良いことになります。

■　端子電圧を求める。

求める端子電圧　\(V\)　は、ミルマンの定理から

\(V=\cfrac{I}{G}\)\(=\cfrac{\cfrac{168}{30}}{\cfrac{14}{30}}\)\(=\cfrac{168}{14}=12\)　[V]

このように、ミルマンの定理ではコンダクタンスと電流を、回路ごとに求めて計算すれば良いので簡単です。

問題2

図の回路において、電圧 \(V\) と各枝路の電流　\(I_1、I_2、I_3\)　を求める。

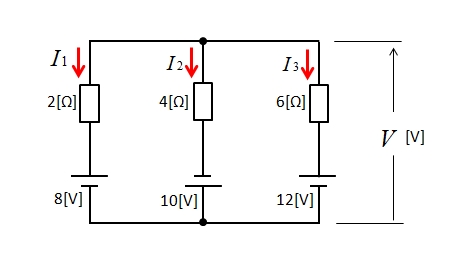
＜解答例＞

端子電圧を求める。

■　合成コンダクタンスを求める。

ミルマンの定理の、合成コンダクタンス　\(G\)　は

\(G=\cfrac{1}{2}+\cfrac{1}{4}+\cfrac{1}{6}\)\(=\cfrac{6+3+2}{12}=\cfrac{11}{12}\)

■　合成電流を求める。

ミルマンの定理の合成電流　\(I\)　は

\(I=\cfrac{8}{2}-\cfrac{10}{4}+\cfrac{12}{6}=\cfrac{42}{12}\)

■　端子電圧　\(V\)　を求める。

\(V=\cfrac{I}{G}\)　の式から

\(V=\cfrac{\cfrac{42}{12}}{\cfrac{11}{12}}=\cfrac{42}{11}\)　[V]　になります。

中央の起電力は、他の起電力と向きが逆になっているので、他の起電力の向きを「正」としたら、中央の起電力の向きは「負」にしなければなりません。

各枝路の電流を求める

■　電流 \(I_1\) を求める。

電流　\(I_1\)　を求めるには、次のように考えれば良いことになります。

端子電圧　\(V\)　は　\(8\)　[V]　と　\(2\)　[Ω]　の電圧降下の合計です。

したがって、\(V=8+2I_1\)

\(I_1=\cfrac{1}{2}(V-8)=\cfrac{1}{2}(\cfrac{42}{11}-8)\)\(=\cfrac{1}{2}(\cfrac{42-88}{11})=-\cfrac{23}{11}\)　[A]

\(I_1\)　はマイナス符号になりますので、図の向きと反対の向きに流れることになります。

■　電流　\(I_2\)　を求める。

同様にして、\(V=-10+4I_2\)

\(I_2=\cfrac{1}{4}(V+10)=\cfrac{1}{4}(\cfrac{42+110}{11})\)\(=\cfrac{1}{4}(\cfrac{152}{11})=\cfrac{38}{11}\)　[A]　

電流の向きは、図の向きと同じ向きになります。

■　電流　\(I_3\)　を求める。

同様にして、\(V=12+6I_3\)

\(I_3=\cfrac{1}{6}(V-12)=\cfrac{1}{6}(\cfrac{42-132}{11})\)\(=-\cfrac{1}{6}(\cfrac{90}{11})=-\cfrac{15}{11}\)　[A]　

電流　\(I_3\)　の向きは、図の向きと反対の向きになります。

以上で「ミルマンの定理」の説明を終わります。