ノートンの定理と使い方

2024年6月9日

ノートンの定理は求めるものが、電圧の時に役立つ定理です。求めるものが電流の時に使う定理は、テブナンの定理です。

この記事は、ノートンの定理の手順と使い方を説明します。

ノートンの定理とは
ノートンの定理の使い方のイメージ
1. 電源の扱い方
ノートンの定理の使い方
練習問題

ノートンの定理とは

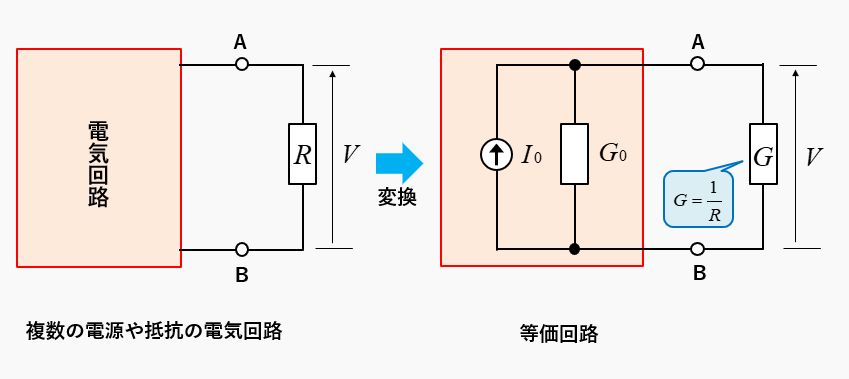
ノートンの定理は、複数の電源や抵抗の電気回路を、電流源と合成コンダクタンスの等価回路に変換して負荷の抵抗に掛かる電圧を求める定理です。

ノートンの定理

$V = \frac{I_{0}}{G_{0} + G}$ [V]

$V$ ・・・求める電圧
$I_{0}$ ・・・短絡電流
$G_{0}$ ・・・合成コンダクタンス
$G$ ・・・負荷のコンダクタンス

ノートンの定理は、短絡電流と合成コンダクタンスを求めて等価回路に変換します。

ノートンの定理の使い方のイメージ

ノートンの定理の使い方のイメージ

ノートンの定理の例題

ノートンの定理で、抵抗 $R$ に掛かる電圧 $V$ を求める。

手順1　切り離す

抵抗 $R$ を切り離す。

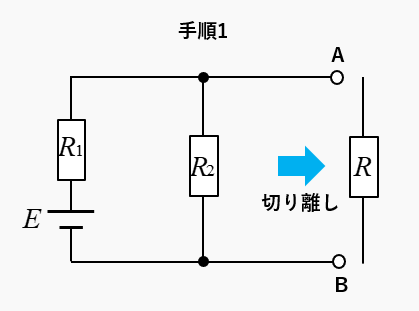
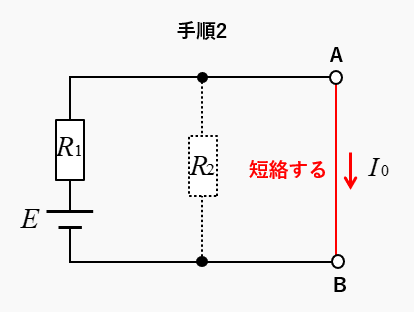
手順2　短絡電流を求める

端子ABを短絡して、流れる電流 $I_{0}$ を求める
端子ABを短絡するので、 $R_{2}$ は無くなる。

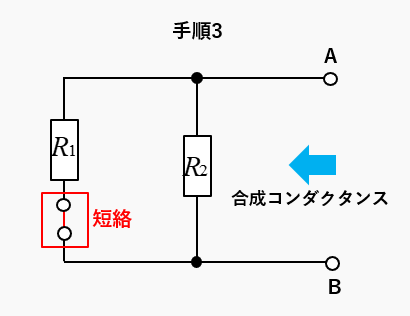
手順3　合成コンダクタンスを求める

電圧源を短絡して、電源を除去する。
端子ABから見た、合成コンダクタンスを求める。
合成コンダクタンス
$G_{0} = \frac{1}{R_{0}}$

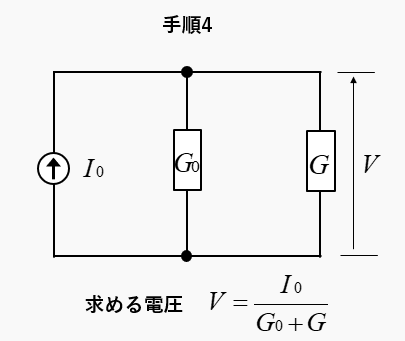
手順4　等価回路に変換

短絡電流と合成コンダクタンスで等価回路に変換
求める電圧 $V$
$V = \frac{I_{0}}{G_{0} + G}$

電源の扱い方

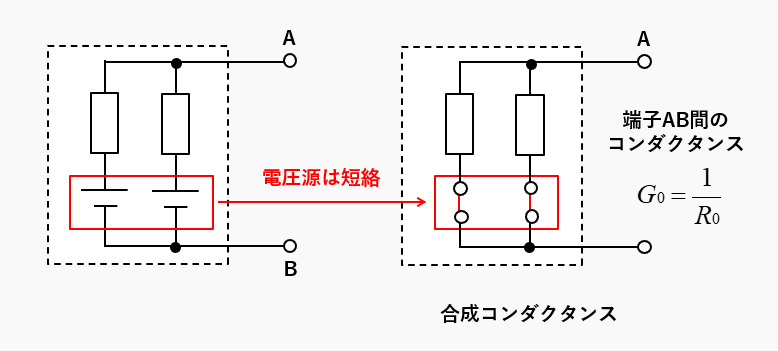
電圧源は短絡する

回路内部の電圧源をすべて短絡し、端子AB間のコンダクタンスが合成コンダクタンスです。

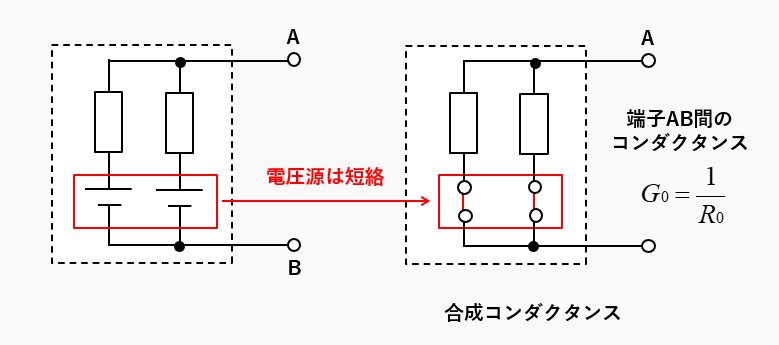
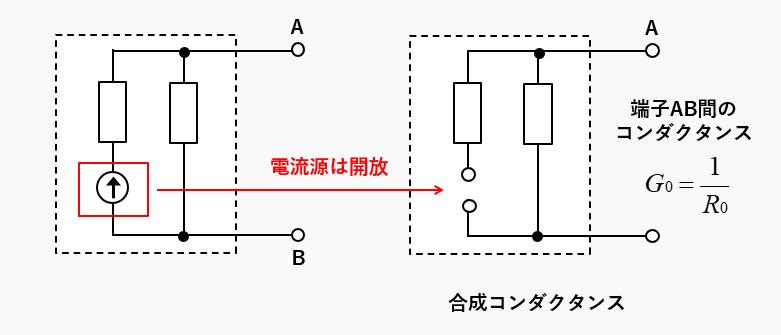
電流源は開放する

回路内部の電流源をすべて開放し、端子AB間のコンダクタンスが合成コンダクタンスです。

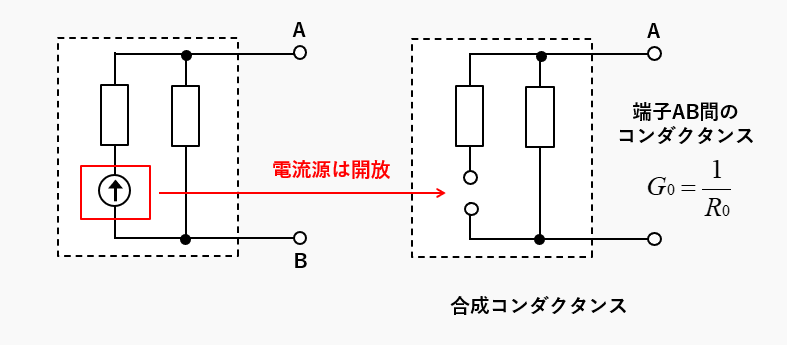
ノートンの定理の使い方

ノートンの定理

$V = \frac{I_{0}}{G_{0} + G}$ [V]

$V$ ・・・求める電圧
$I_{0}$ ・・・短絡電流
$G_{0}$ ・・・合成コンダクタンス
$G$ ・・・負荷のコンダクタンス

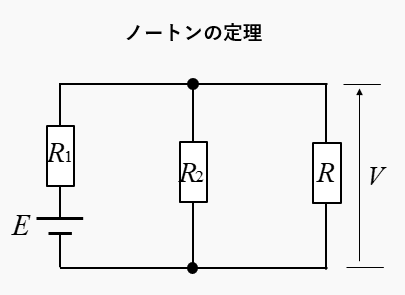
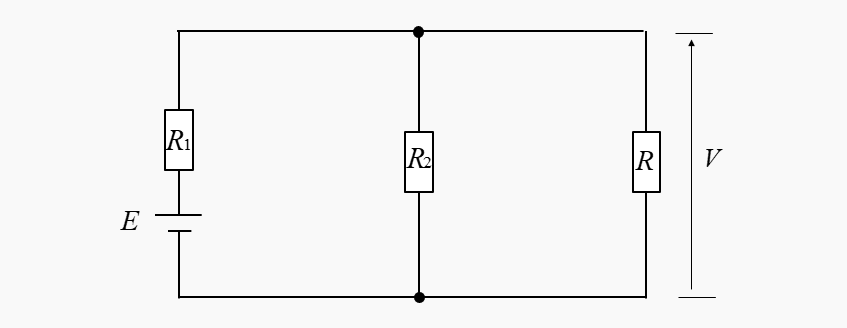
ノートンの定理は、図のような回路の負荷の抵抗に掛かる電圧を求める時に使います。

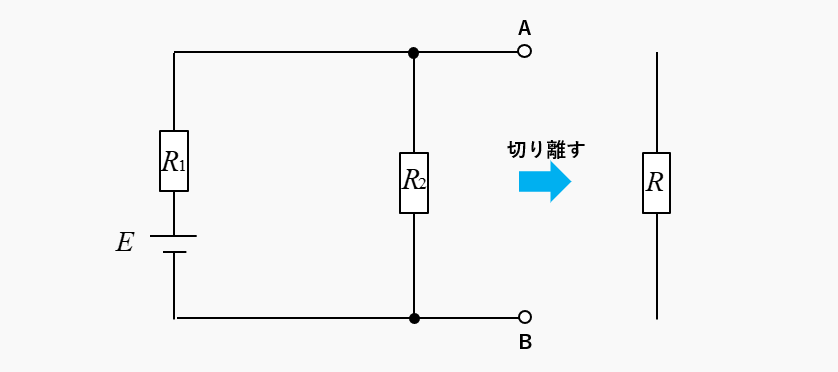
解き方の手順1（抵抗を切り離す）

負荷の抵抗を切り離します。

解き方の手順2（短絡電流を求める）

端子AB間を短絡して、短絡電流を求めます。AB間を短絡すると、 $R_{2}$ は導通するので無いものと同じになります。

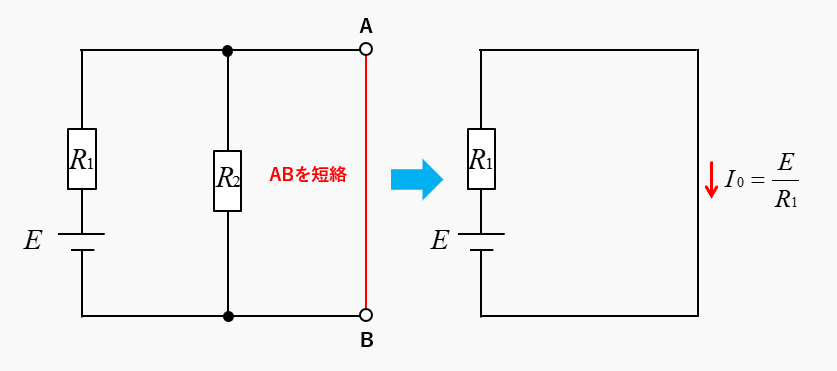
短絡電流は

$I_{0} = \frac{E}{R_{1}}$ [A]

解き方の手順3（合成コンダクタンスを求める）

端子ABから見た時の、合成コンダクタンスを求める。合成コンダクタンスを計算するときには、電圧源は短絡し電流源は開放します。

電圧源は短絡して電源を除去する
電流源は開放して電源を除去する

電圧源は短絡して除去する: 回路内部の電圧源をすべて短絡し、合成コンダクタンスを求める。
電流源は開放して除去する: 回路内部の電流源をすべて開放し、合成コンダクタンスを求める。

電圧源を短絡して合成コンダクタンスを求める

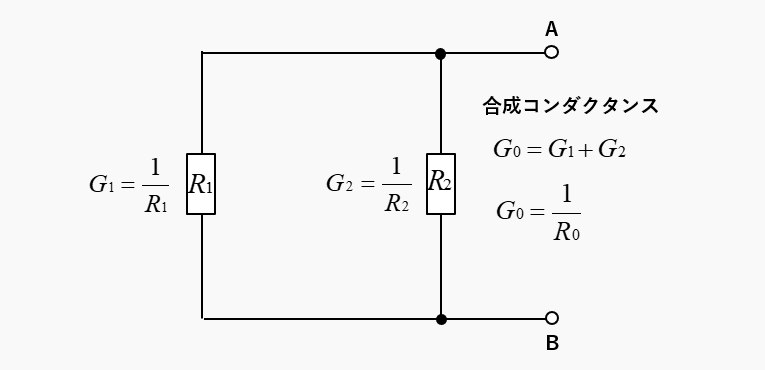
並列接続の抵抗の合成抵抗は、「合成抵抗の逆数の和が抵抗の逆数の和に等しい」ので

$\frac{1}{R_{0}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ になります。コンダクタンスで表すと

$G_{0} = G_{1} + G_{2}$ になります。

コンダクタンスについて

解き方の手順4（等価回路に変換する）

短絡電流と合成コンダクタンスを使って、等価回路に変換します。

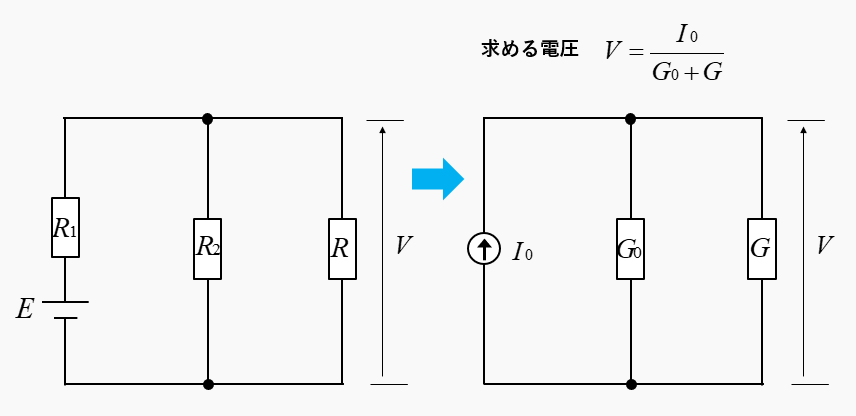
等価回路から抵抗 $R$ の端子電圧は

$V = \frac{I_{0}}{G_{0} + G}$ [V] で求められます。

練習問題

問題1

次の図のような回路について、ノートンの定理で問題を解いてみましょう。

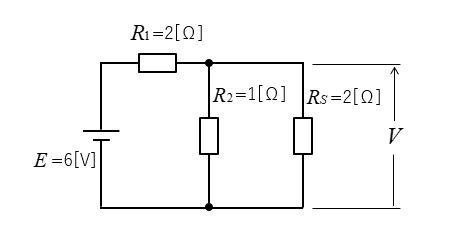
＜解答例＞

■　求めたい部分の抵抗を切り離します。

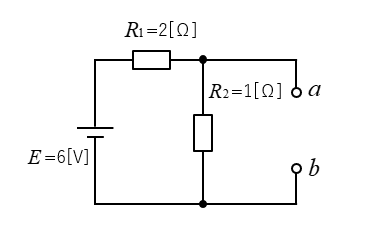
■　合成コンダクタンスを求めます。

回路内部の電源をすべて短絡し、端子 ab 間から見たコンダクタンス $G_{0}$ （抵抗の逆数）を求めます。

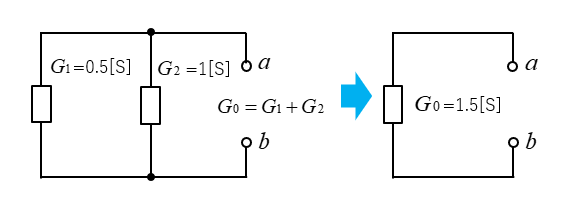
$G_{1} = \frac{1}{2} = 0.5$

$G_{2} = \frac{1}{1} = 1$

$G_{0} = G_{1} + G_{2} = 1.5$ [S]　

■　短絡電流を求める。

抵抗 $R_{S}$ があった部分を短絡させます。

抵抗 $R_{S}$ を短絡させたので、抵抗 $R_{2}$ に流れる電流は $0$ になります。

短絡電流は

$I_{0} = \frac{E}{R_{1}} = \frac{6}{2} = 3$ [A]

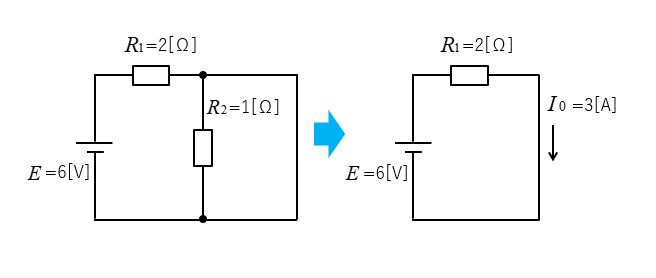
■　等価回路に変換します。

合成コンダクタンスと短絡電流から、元の回路は電流源の回路に変換することができます。

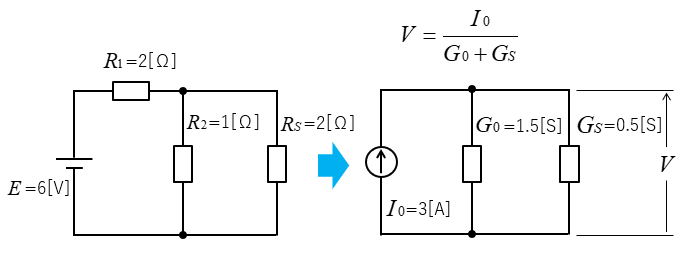
抵抗 $R_{S}$ にかかる電圧は

$V = \frac{I_{0}}{G_{0} + G_{S}} = \frac{3}{2} = 1.5$ [V] になります。

問題2

次の回路の $R_{3}$ にかかる電圧を「ノートンの定理」で求めよ。

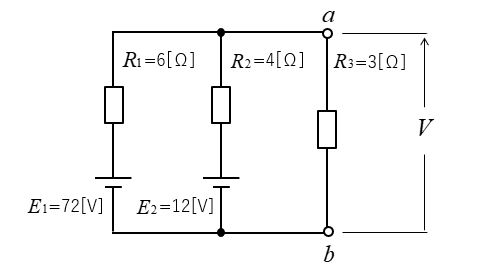
＜解答例＞

■　抵抗　 $R_{3}$ 　を切り離します。

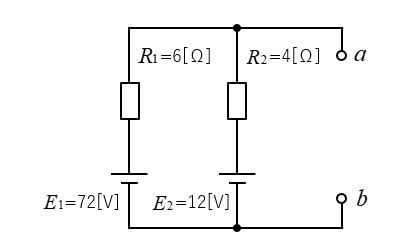
■　合成コンダクタンス $G_{0}$ を求める。（回路内部の電源をすべて短絡する）

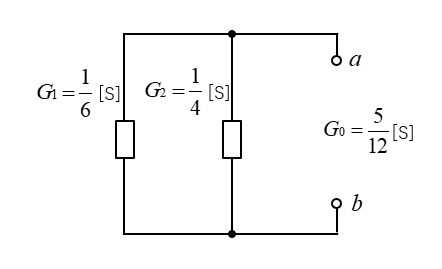
$G_{0} = G_{1} + G_{2}$

$G_{0} = \frac{1}{6} + \frac{1}{4} = \frac{5}{12}$ [S]　

■　短絡電流　 $I_{0}$ 　を求める。

電圧を求めたいところの抵抗を短絡します。

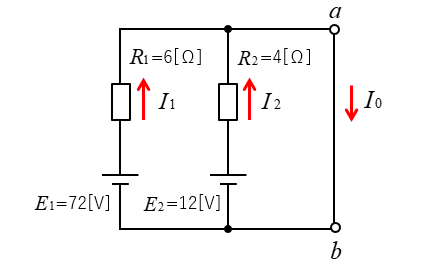
$I_{0} = I_{1} + I_{2} = \frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}$

$I_{0} = \frac{72}{6} + \frac{12}{4} = 15$ [A]　

■　等価回路に変換します。

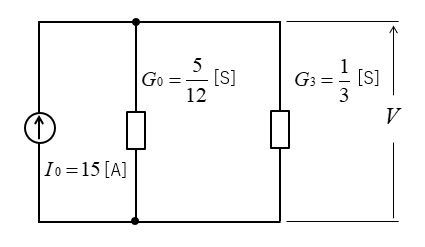
$V = \frac{I_{0}}{G_{0} + G_{3}}$

$V = \frac{15}{\frac{5}{12} + \frac{1}{3}} = 20$ [V]

したがって、抵抗 $R_{3}$ にかかる電圧は、 $20$ [V] になります。

問題3

次の回路の、抵抗　 $R$ 　にかかる電圧 $V$ をノートンの定理で求めよ。

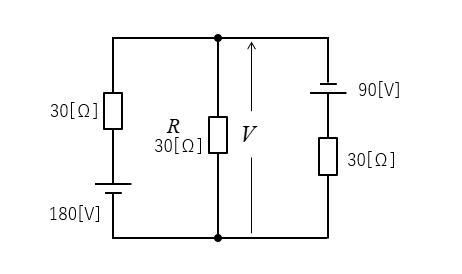
＜解答例＞

■　抵抗 $R$ を切り離します。

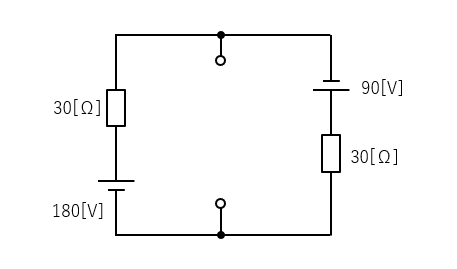
■　合成コンダクタンス $G_{0}$ を求める。（回路内部の電源をすべて短絡する）

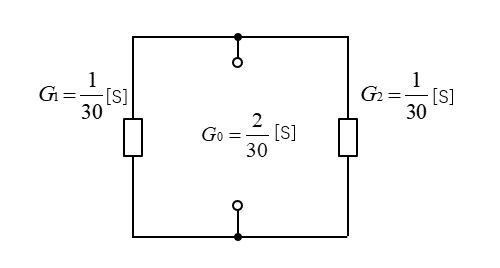
$G_{0} = G_{1} + G_{2}$

$G_{0} = \frac{1}{30} + \frac{1}{30} = \frac{2}{30}$ [S]

■　短絡電流　 $I_{0}$ 　を求める。

電圧を求めたいところの抵抗を短絡します。電流の向きを図のように仮定します。

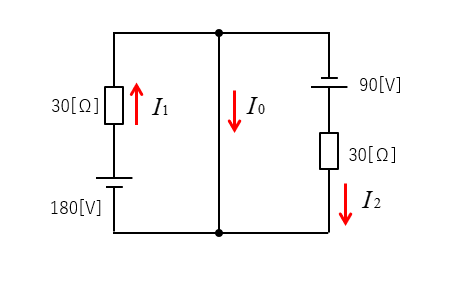
$I_{1} = I_{0} + I_{2}$ 　から　 $I_{0} = I_{1} - I_{2}$

$I_{0} = \frac{180}{30} - \frac{90}{30} = 3$ [A]

■　等価回路に変換します。

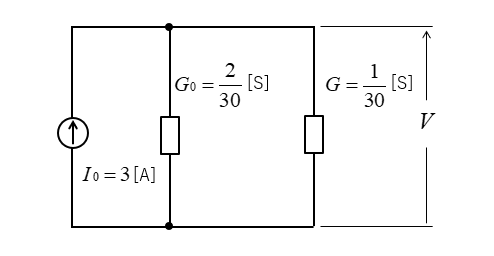
$V = \frac{I_{0}}{G_{0} + G}$

$V = \frac{3}{\frac{2}{30} + \frac{1}{30}} = 30$ [V]

したがって、抵抗 $R$ にかかる電圧は、 $30$ [V] になります。

問題4

次の回路の $R$ にかかる電圧をノートンの定理で求めよ。

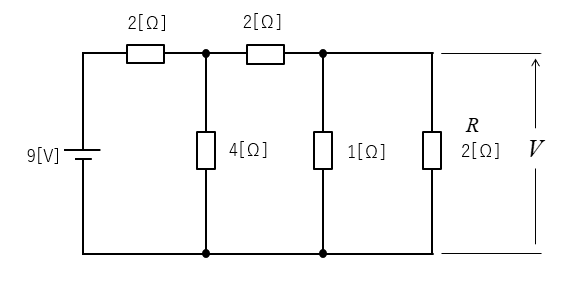
＜解答例＞

■　抵抗　 $R$ 　を切り離します。

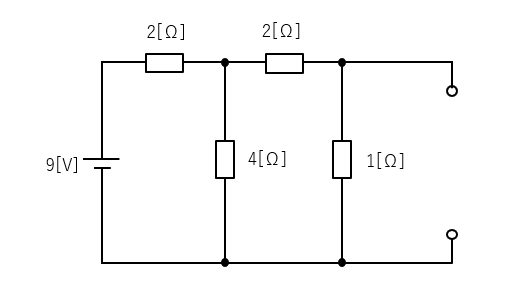
■　合成コンダクタンス $G_{0}$ を求める。（回路内部の電源をすべて短絡する）

コンダクタンス似する前に、抵抗を整理する。

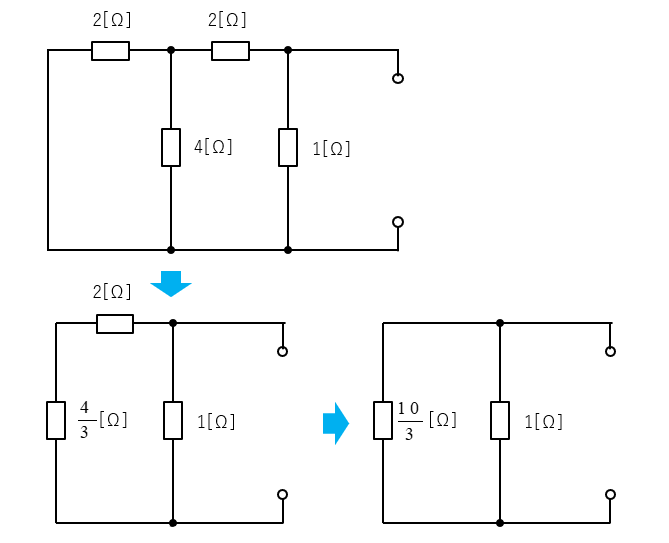
■　合成コンダクタンス $G_{0}$ を求める。

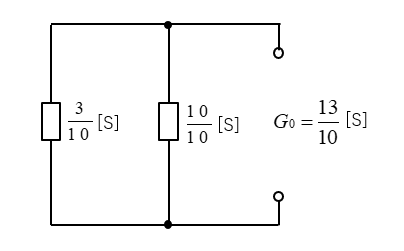
$G_{0} = \frac{3}{10} + \frac{10}{10} = \frac{13}{10}$ [S]　

■　短絡電流 $I_{0}$ を求める。

電圧を求めたいところの抵抗を短絡します。

抵抗 $R$ を短絡するので、 $1$ [Ω] の抵抗は無いものと同じになります。

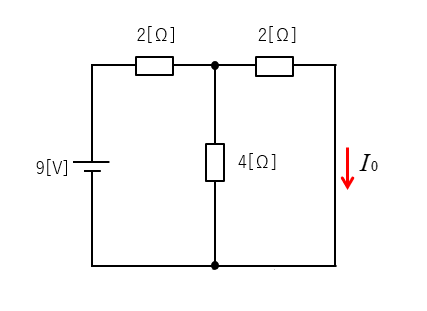
回路に流れる電流は

$I = \frac{9}{2 + \frac{2 \times 4}{2 + 4}}$

$I = \frac{9}{\frac{6}{3} + \frac{4}{3}}$

$I = \frac{27}{10}$

分流の法則を使って

$I_{0} = \frac{27}{10} \times \frac{4}{6} = \frac{9}{5}$ 　[A]　になります。

■　等価回路に変換します。

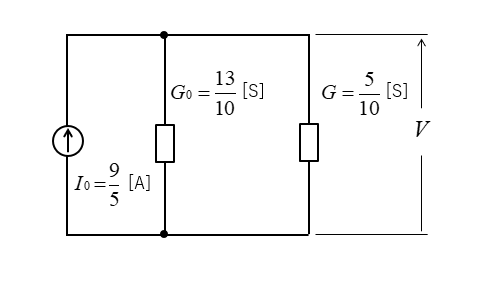
$V = \frac{I_{0}}{G_{0} + G}$

$V = \frac{9}{5} \times \frac{1}{\frac{13}{10} + \frac{5}{10}}$

$V = \frac{9}{5} \times \frac{10}{18} = 1$ [V]

したがって、抵抗 $R$ にかかる電圧は、 $1$ [V] になります。

関連記事

任意の場所に流れる電流を求める定理は、テブナンの定理です

テブナンの定理の使い方【任意の場所に流れる電流を求める定理】

複数の電源と抵抗の並列回路の、端子電圧を求める

ミルマンの定理

以上で「ノートンの定理と使い方」の説明を終わります。