テブナンの定理の問題を集めました。
テブナンの定理の問題を解くことで、テブナンの定理を理解します。
練習問題
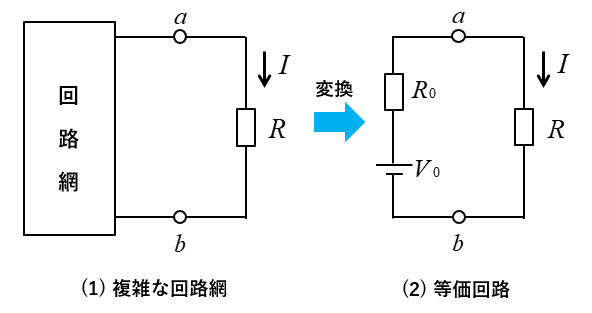
- 電流を求めたい部分を切り離します。
- 等価電源 \(V_0\) を求める。
- 等価抵抗 \(R_0\) を求める。(回路内部の電源をすべて短絡する)
- 等価回路に変換する。
- 目的の電流 \(I=\cfrac{V_0}{R_0+R}\quad\rm[A]\) を求める。
問題1
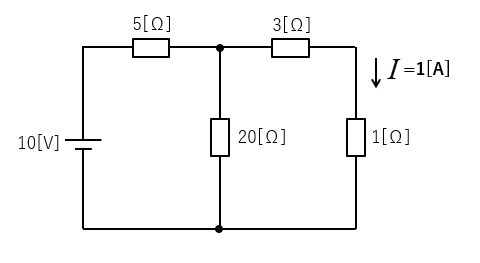
テブナンの定理で 1[Ω] の抵抗に流れる電流を求めよ。
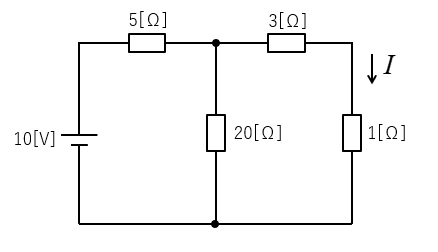
<解 答>
1.電流を求めたい部分を切り離します。
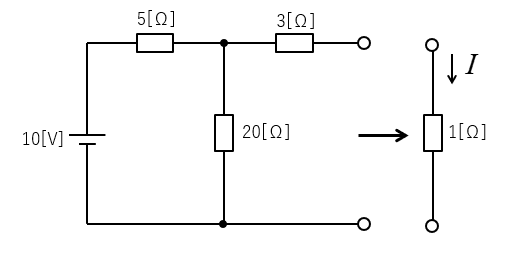
2.等価電源 \(V_0\) を求める。
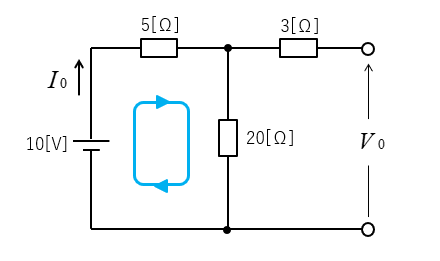
電流 \(I_0\) を求める。
\(I_0=\cfrac{10}{5+20}=0.4\) [A]
等価電源 \(V_0\) を求める。
\(V_0=10-5×0.4=8\) [V]
または、\(V_0=20×0.4=8\) [V]
3.等価抵抗 \(R_0\) を求める。
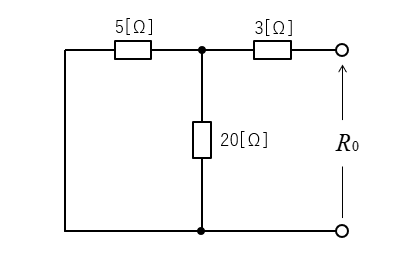
抵抗の直並列接続です。
\(R_0=3+\cfrac{5×20}{5+20}=7\) [Ω]
4.等価回路に変換する。
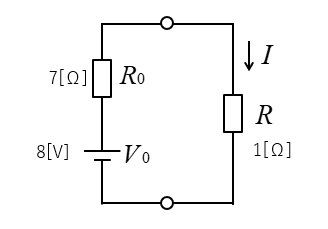
求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}=\cfrac{8}{8}=1\) [A] になります。
問題2
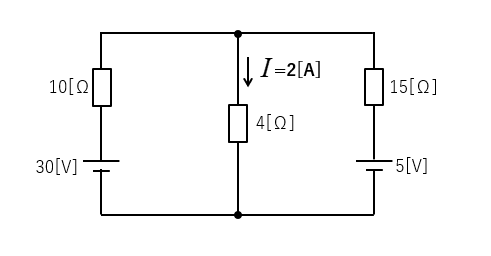
テブナンの定理で 4[Ω] の抵抗に流れる電流を求めよ。
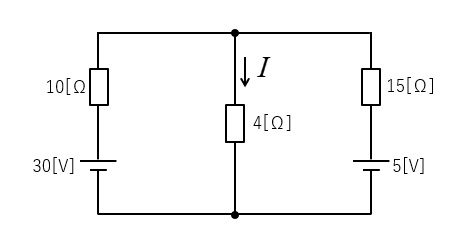
<解 答>
1.電流を求めたい部分を切り離します。
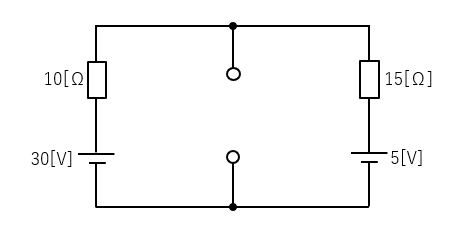
2.等価電源 \(V_0\) を求める。
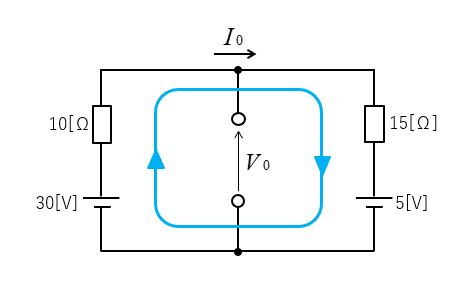
電流 \(I_0\) を求める。
\(I_0=\cfrac{30-5}{10+15}=1\) [A]
等価電源 \(V_0\) を求める。
\(V_0=30-10×1=20\) [V]
または、\(V_0=5+15×1=20\) [V]
3.等価抵抗 \(R_0\) を求める。
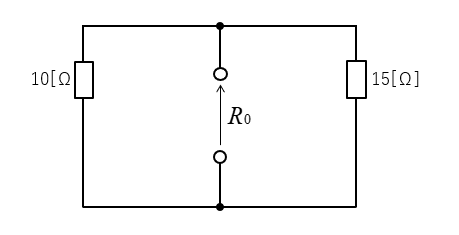
抵抗の並列接続です。
\(R_0=\cfrac{10×15}{10+15}=6\) [Ω]\)
4.等価回路に変換する。
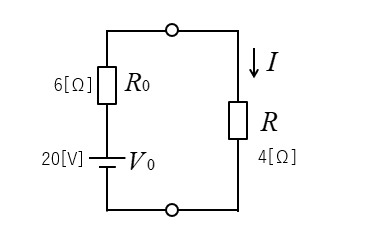
求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}=\cfrac{20}{10}=2\) [A] になります。
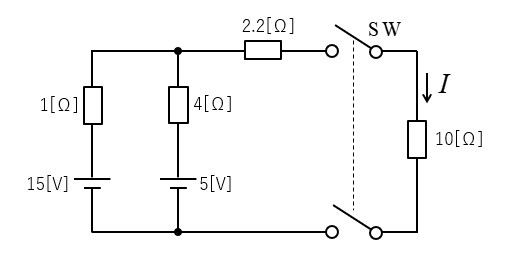
問題3
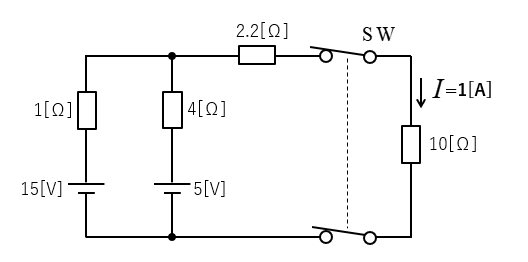
SWを閉じた時に 10[Ω] の抵抗に流れる電流を求めよ。
<解 答>
1.電流を求めたい部分を切り離します。
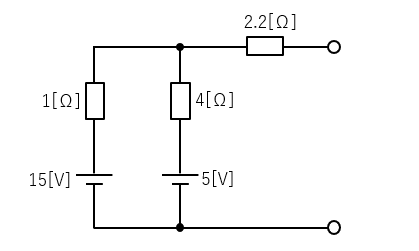
2.等価電源 \(V_0\) を求める。
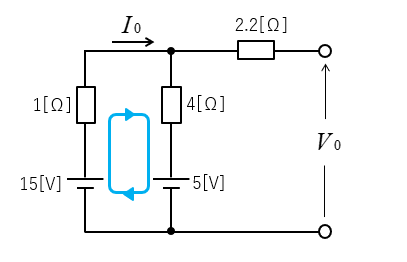
電流 \(I_0\) を求める。
\(I_0=\cfrac{15-5}{1+4}=2\) [A]
等価電源 \(V_0\) を求める。
\(V_0=15-1×2=13\) [V]
または、\(V_0=5+4×2=13\) [V]
3.等価抵抗 \(R_0\) を求める。
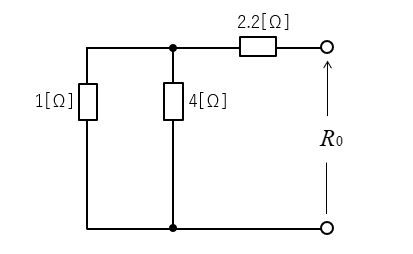
抵抗の直並列接続です。
\(R_0=2.2+\cfrac{1×4}{1+4}=3\) [Ω]
4.等価回路に変換する。
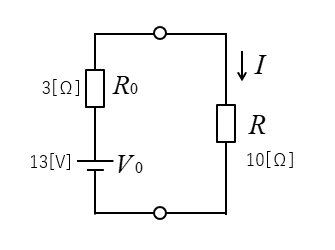
求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}=\cfrac{13}{13}=1\) [A] になります。
問題4
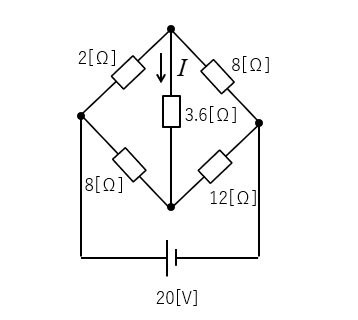
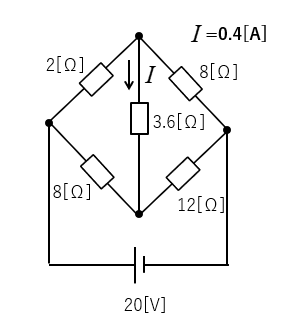
テブナンの定理で電流 \(I\) を求めよ。(ブリッジ回路)
<解 答>
1.電流を求めたい部分を切り離します。
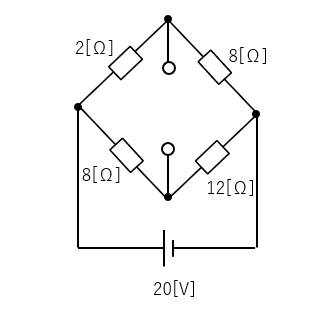
2.等価電源 \(V_0\) を求める。
\(V_0\) は端子ab間の電位差になります。
わかり易くするために、回路を変形します。
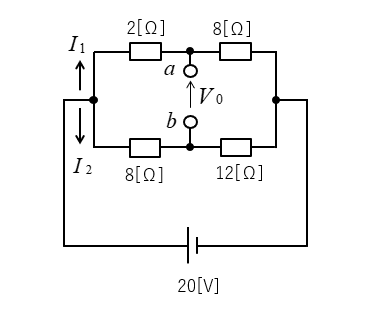
電流 \(I_1、I_2\) を求める。
\(I_1=\cfrac{20}{2+8}=2\) [A]
\(I_2=\cfrac{20}{8+12}=1\) [A]
aの電位を \(V_a\)、bの電位を \(V_b\) とすると
\(V_a=20-2×2=16\) [V]
\(V_b=20-8×1=12\) [V]
等価電源 \(V_0\) を求める。
\(V_0=V_a-V_b=16-12=4\) [V]
3.等価抵抗 \(R_0\) を求める。
図を見やすくします。
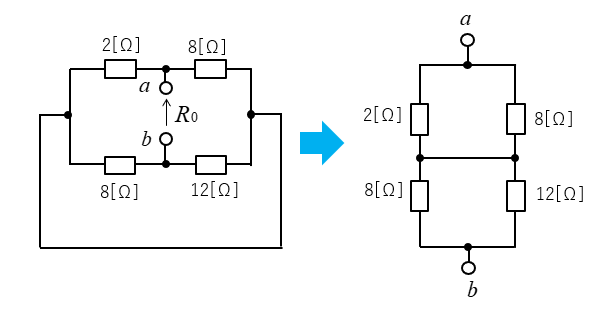
抵抗の直並列接続です。
\(R_0=\cfrac{2×8}{2+8}+\cfrac{8×12}{8+12}=6.4\) [Ω]
4.等価回路に変換する。
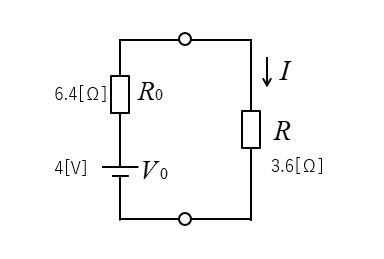
求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}=\cfrac{4}{10}=0.4\) [A] になります。
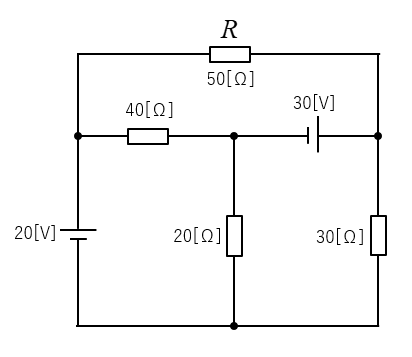
問題5
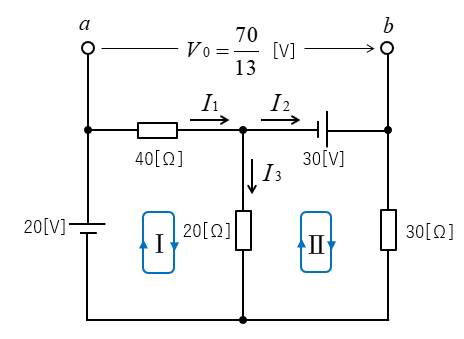
\(R\) 50[Ω] に流れる電流の大きさと方向を求めよ。
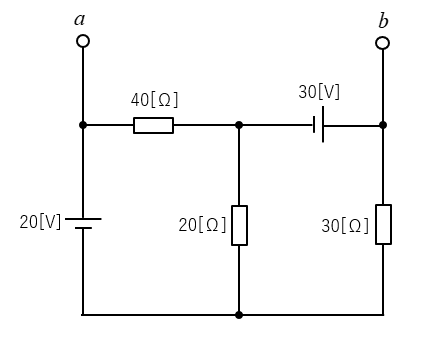
<解 答>
1.電流を求めたい部分を切り離します。
2.等価電源 \(V_0\) を求める。
回路Ⅰと回路Ⅱに分割して計算します。
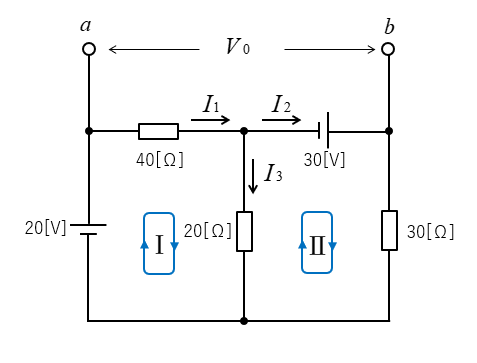
回路Ⅰの計算
次の計算式が成り立ちます。
\(20=40I_1+20I_3\cdots(1)\)
\(I_3=I_1-I_2\cdots(2)\)
式(2)を式(1)に代入して整理する。
\(I_2=3I_1-1\cdots(3)\)
回路Ⅰの計算
\(30=30I_2-20I_3\cdots(4)\)
式(2)を式(4)に代入して整理する。
\(3=5I_2-2I_1\cdots(5)\)
式(3)を式(5)に代入して整理する。
\(3=5(3I_1-1)-2I_1\)
\(I_1=\cfrac{8}{13}\) [A]
\(I_2=\cfrac{11}{13}\) [A]
\(V_{ab}\) を正の向きと考えると
\(V_{ab}=40I_1-30=40×\cfrac{8}{13-30}=-\cfrac{70}{13}\) [V]
\(V_{ab}\) がマイナスになるので、b点の電位が高いことになります。
3.等価抵抗 \(R_0\) を求める。
図を見やすく整理すると、並列接続です。
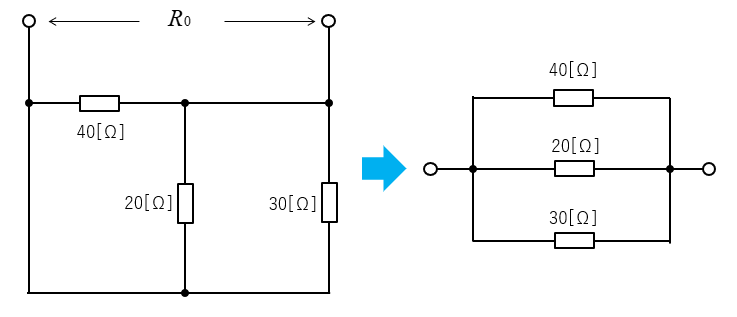
\(\cfrac{1}{R_0}=\cfrac{1}{40}+\cfrac{1}{20}+\cfrac{1}{30}\)
\(R_0=\cfrac{120}{13}\) [Ω]
4.等価回路に変換する。
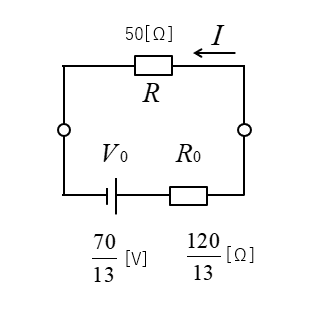
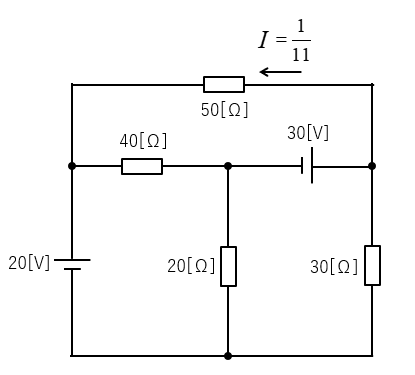
\(I=\cfrac{V_0}{R_0+R}\)\(=\cfrac{70}{13}×\cfrac{1}{\cfrac{120}{13}+50}\)
\(I=\cfrac{1}{11}≒0.091\) [A] になります。
電流の向きは、左向きになります。
問題6
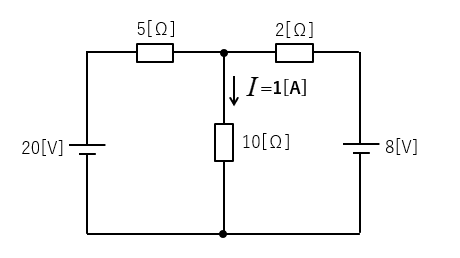
テブナンの定理で 10[Ω] の抵抗に流れる電流を求めよ。
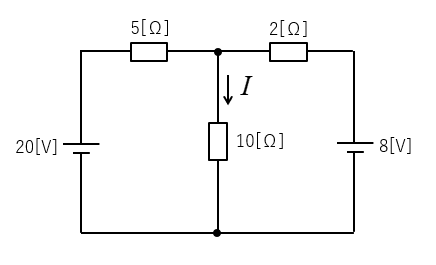
<解 答>
1.電流を求めたい部分を切り離します。
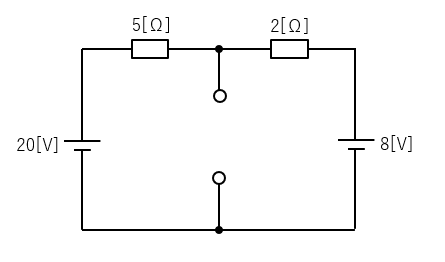
2.等価電源 \(V_0\) を求める。
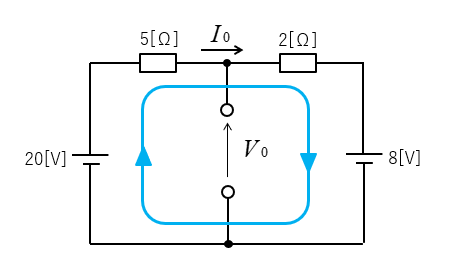
電流 \(I_0\) を求める。
\(I_0=\cfrac{20-8}{2+5}=\cfrac{12}{7}\) [A]
等価電源 \(V_0\) を求める。
\(V_0=20-\cfrac{12×5}{7}=\cfrac{80}{7}\) [V]
または、\(V_0=8+\cfrac{12×2}{7}=\cfrac{80}{7}\) [V]
3.等価抵抗 \(R_0\) を求める。
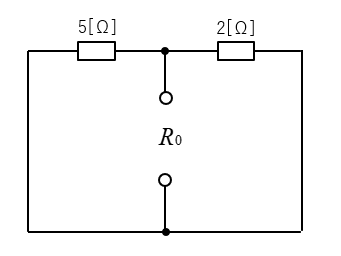
抵抗の並列接続です。
\(R_0=\cfrac{5×2}{5+2}=\cfrac{10}{7}\) [Ω]
4.等価回路に変換する。

求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}=\cfrac{80}{7}×\cfrac{1}{10+\cfrac{10}{7}}=1\) [A] になります。
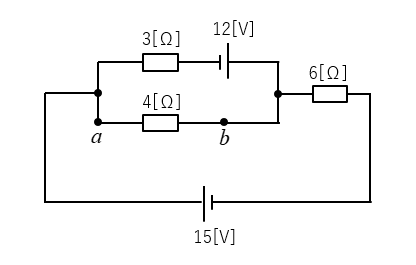
問題7
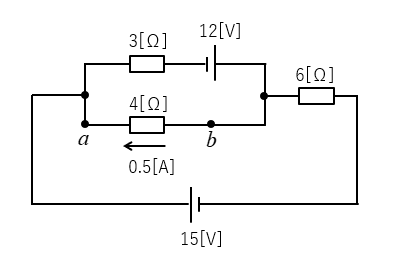
回路図のab間の抵抗 4[Ω] に流れる電流を求めよ。
<解 答>
1.電流を求めたい部分を切り離します。
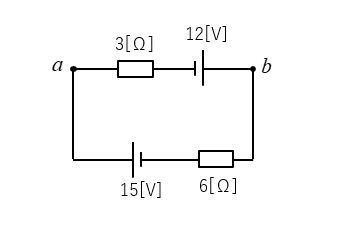
2.等価電源 \(V_0\) を求める。
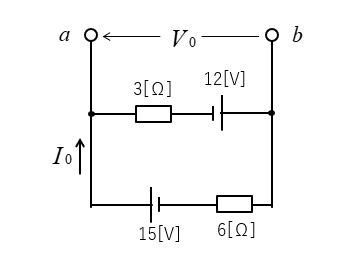
電流 \(I_0\) を求める。
\(I_0=\cfrac{15+12}{3+6}=3\) [A]
等価電源 \(V_{ab}\) を求める。
\(V_{ab}=15-6×3=-3\) [V]
または、\(V_{ab}=3×3-12=-3\) [V]
\(V_{ba}=V_0\) とすると
\(V_0=3\) [V]
3.等価抵抗 \(R_0\) を求める。
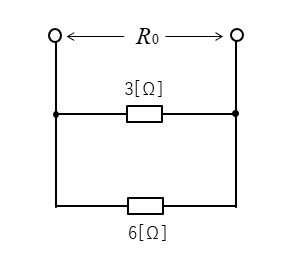
抵抗の並列接続です。
\(R_0=\cfrac{3×6}{3+6}=2\) [Ω]
4.等価回路に変換する。
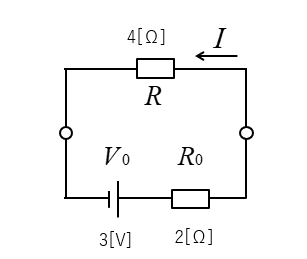
求める電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}=\cfrac{3}{6}=0.5\) [A]
図で示すと次のようになります。
問題 8
テブナンの定理 で、次の問題の抵抗 \(R\) を求めなさい。
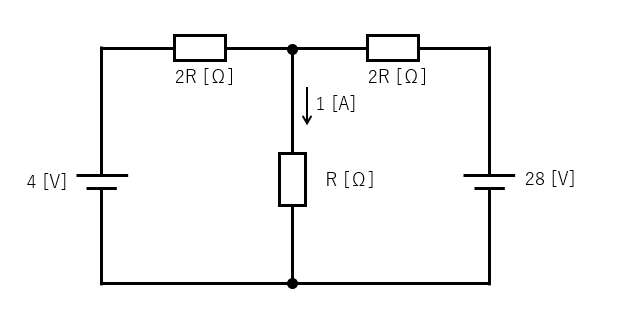
<解答例>
抵抗 \(R\) を切り放します。
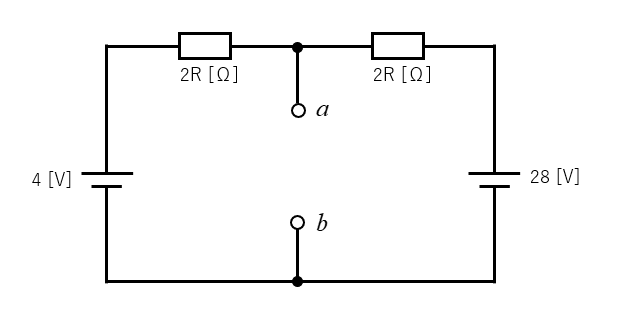
端子ab間の \(V_0\) を求めます。
回路に流れる電流を \(I_0\) とします。
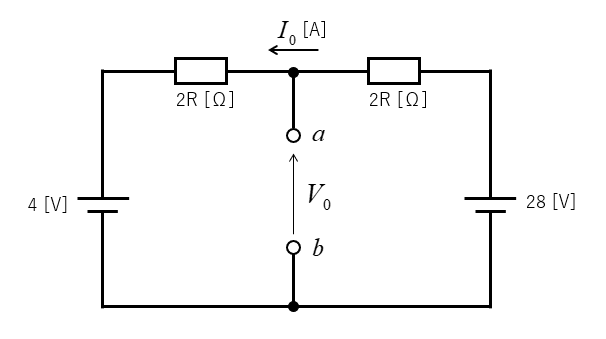
\(I_0=\cfrac{28-4}{4R}=\cfrac{24}{4R}\)
\(V_0=28-2RI_0=28-2R(\cfrac{24}{4R})=16\)
端子ab間の \(R_0\) を求めます。
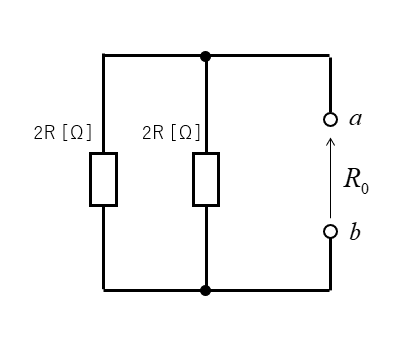
\(2R\) の並列抵抗なので、和分の積から
\(R_0=R\) になります。
テブナンの定理より抵抗Rに流れる電流 \(I\) は
\(I=\cfrac{V_0}{R_0+R}=\cfrac{16}{2R}=1\) [A]
\(R=8\) [Ω]
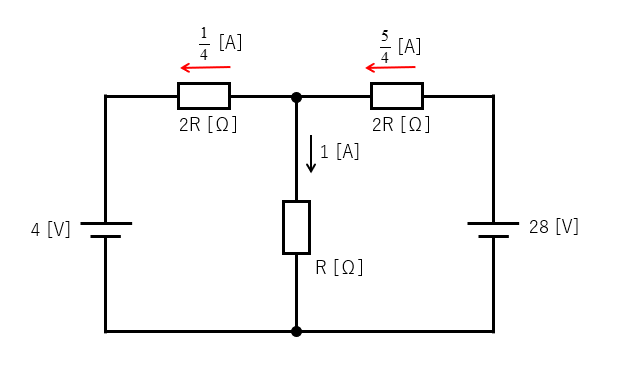
\(2R\) の抵抗に流れる電流を図のように仮定します。
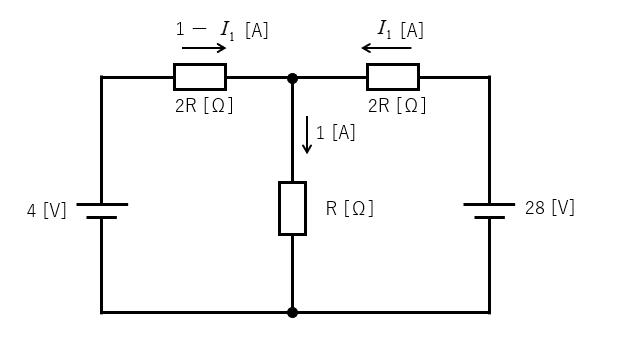
次の式が成り立ちます。
\(28=2RI_1+R×1\)
\(28=2×8×I_1+8\)
\(16I_1=20\)
\(I_1=\cfrac{5}{4}\) [A]
\(1-I_1=-\cfrac{1}{4}\) [A]
回路に流れる電流は図のようになります。
左側の回路には仮定した方向と逆向きに流れます。
以上で「テブナンの定理の問題集」の説明を終わります。