この記事では
- 枝電流法
- ループ電流法
- 重ね合わせの理
- テブナンの定理
- ミルマンの定理
による問題の解析を比較します。
同じ問題を、それぞれの解き方で行い比較します。
枝電流法による解析
【キルヒホッフの法則により、次の回路の各枝電流を求めよ。】
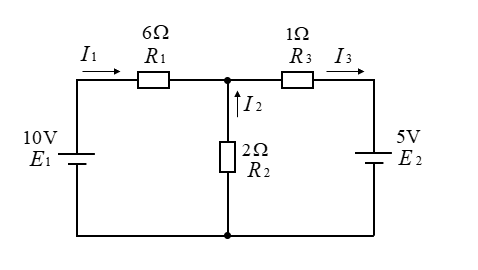
■ 節点Pの電流関係から
\(I_1+I_2=I_3\cdots(1)\) になります。

閉回路Aの式を立てる。
\(6I_1-2I_2=10\cdots(2)\)
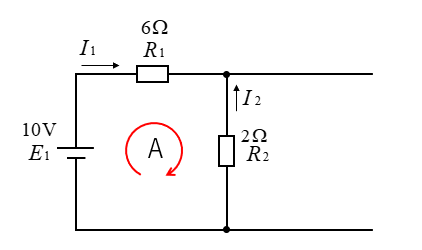
閉回路Bの式を立てる。
\(2I_2+I_3=-5\cdots(3)\)
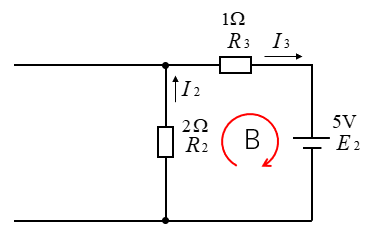
式(3)に式(1)を代入して \(I_3\) を消去します。
\(I_1+3I_2=-5\cdots(4)\)
式を解いて \(I_1、I_2\) を求めます。
\(I_1=1\quad\rm[A]\)
\(I_2=-2\quad\rm[A]\)
式(1)より
\(I_3=-1\quad\rm[A]\) になります。
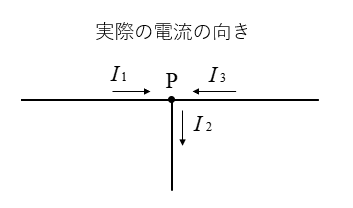
■ 電流値のマイナス記号
電流の値がマイナスになるときは、初めに設定した電流の向きと反対の方向に流れていることを示しています。
ループ電流法による解析
図のようにループ電流を \(I_1、I_2\) とします。
まん中には、\(I_1-I_2\) が下向きに流れると仮定します。
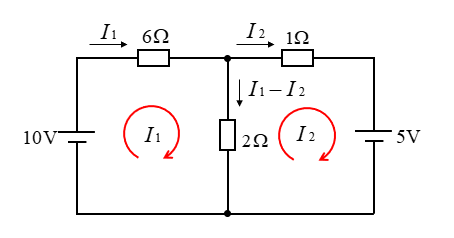
■ ループ \(I_1\)
\(6I_1+2(I_1-I_2)=10\) から
\(4I_1-I_2=5\cdots(1)\)
■ ループ \(I_2\)
\(-2(I_1-I_2)+I_2=-5\)
\(3I_2=2I_1-5\cdots(2)\)
式(1)の両辺に3を掛けます。
\(12I_1-3I_2=15\cdots(3)\)
式(3)に式(2)を代入します。
\(12I_1-(2I_1-5)=15\) から
\(I_1=1\) [A]
\(I_2=-1\) [A]
まん中に流れる電流 \(I_1-I_2\) は、次のようになります。
\(I_1-I_2=1-(-1)=2\) [A] になります。
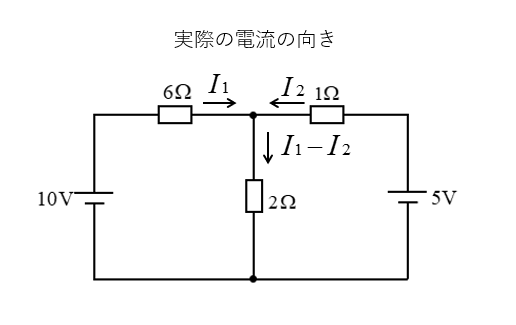
重ね合わせの理
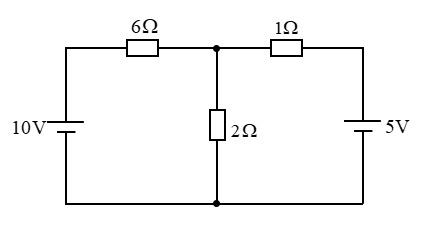
■ \(\rm 10V\) の電源を残して考えて \(\rm 5V\) の電源は短絡します。
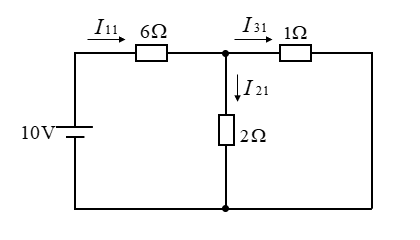
合成抵抗は
\(R_1=6+\cfrac{2×1}{2+1}=\cfrac{20}{3}\) [Ω]
電流 \(I_{11}\) は
\(I_{11}=\cfrac{10×3}{20}=\cfrac{3}{2}\) [A]
並列部分の電流は、「分流の法則」により
\(I_{21}=\cfrac{3}{2}×\cfrac{1}{2+1}=\cfrac{1}{2}\) [A]
\(I_{31}=\cfrac{3}{2}×\cfrac{2}{2+1}=1\) [A]
■ \(\rm 5V\)の電源を残して \(\rm 10V\) の電源は短絡します。
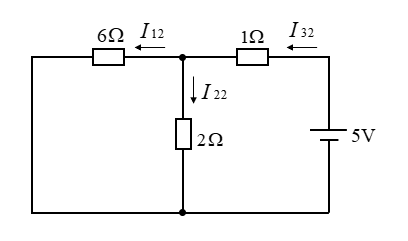
合成抵抗は
\(R_2=1+\cfrac{6×2}{6+2}=\cfrac{5}{2}\) [Ω]
電流 \(I_{32}\) は
\(I_{32}=\cfrac{5×2}{5}=2\) [A]
並列部分の電流は、「分流の法則」により
\(I_{12}=2×\cfrac{2}{6+2}=\cfrac{1}{2}\) [A]
\(I_{22}=2×\cfrac{6}{6+2}=\cfrac{3}{2}\) [A]
最後に回路1と回路2の各電流を「重ね合わせ」ます。
\(I_{11}-I_{12}=\cfrac{3}{2}-\cfrac{1}{2}=1\) [A]
\(I_{21}+I_{22}=\cfrac{1}{2}+\cfrac{3}{2}=2\) [A]
\(I_{31}-I_{32}=1-2=-1\) [A]
テブナンの定理による解析
図の \(2Ω\) の抵抗に流れる電流 \(I\) を、テブナンの定理で求めよ。

■ テブナンの定理を使うために、回路を変形します。
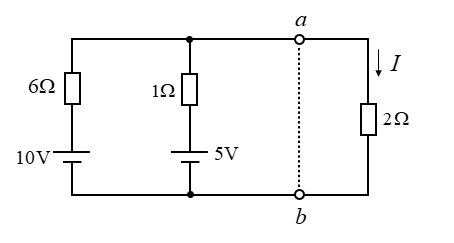
等価電源 \(V_0\) を求めるために、\(ab\) 間で切り離します。
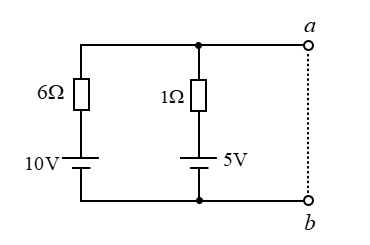
閉回路の \(I_0\) を求めます。

\(I_0=\cfrac{10-5}{6+1}=\cfrac{5}{7}\) [A]
等価電源は
\(V_0=10-\cfrac{5×6}{7}=\cfrac{40}{7}\) [V]
または
\(V_0=5+\cfrac{5×1}{7}=\cfrac{40}{7}\) [V]
等価抵抗は、電源を短絡して次のようになります。
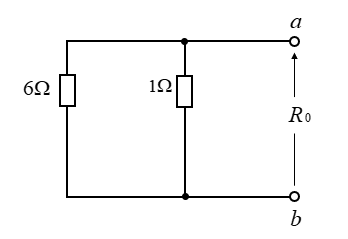
\(R_0=\cfrac{6×1}{6+1}=\cfrac{6}{7}\) [Ω]
等価回路に切り離しておいた、\(2Ω\) を接続したときに流れる電流は次のようになります。
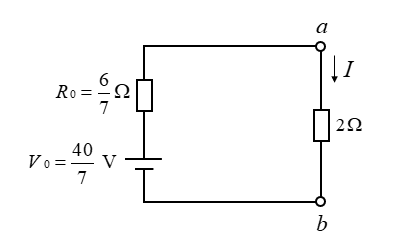
\(I=\cfrac{V_0}{R_0+2}=\cfrac{40}{7}×\cfrac{7}{20}=2\) [A]
ミルマンの定理による解析
図の各枝路に流れる電流をミルマンの定理で求めよ。
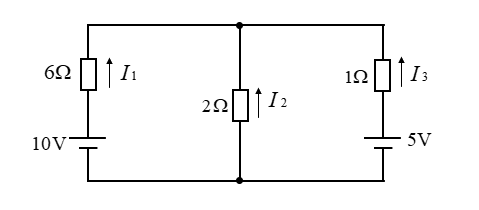
■ ミルマンの定理より
\(V=\cfrac{I}{G}\)=\(\cfrac{ \displaystyle \sum _{ i=1 }^n\cfrac{E_i}{R_i}}{\displaystyle \sum_{i=1}^n\cfrac{1}{R_i}}\) [V]
\(V=\cfrac{\cfrac{10}{6}+\cfrac{0}{2}+\cfrac{5}{1}}{\cfrac{1}{6}+\cfrac{1}{2}+\cfrac{1}{1}}\)\(=\cfrac{\cfrac{40}{6}}{\cfrac{10}{6}}=4\) [V]
各枝路の電流
\(4=10-6I_1\) より \(I_1=1\) [A]
\(4=0-2I_2\) より \(I_2=-2\) [A]
\(I_2\) はマイナスなので、図の向きと逆になります。
\(4=5-1×I_3\) より \(I_3=1\) [A]
以上で「各枝電流の解析例」の説明を終わります。