分流の法則とは、並列回路の抵抗に分流する電流の法則です。抵抗の大きさの逆数に比例して、回路に流れる電流が分流することを、電流の分流と呼びます。
分流の法則は、回路に流れる電流がそれぞれの抵抗に分流する電流を求める法則
分流の法則

回路に流れる電流が抵抗の大きさの逆数に比例して、電流が分流する法則を「分流の法則」といいます。
分流の法則を式にすると、次のようになります。
\(求める分流の値=\)\(\cfrac{合成抵抗}{求める分流の抵抗}×回路に流れる電流\)
2個の抵抗が並列接続された分流の法則
2個の抵抗が並列接続された場合のそれぞれの抵抗に流れる電流は、回路に流れる電流と各抵抗値が分かれば「分流の法則」で求めることができます。
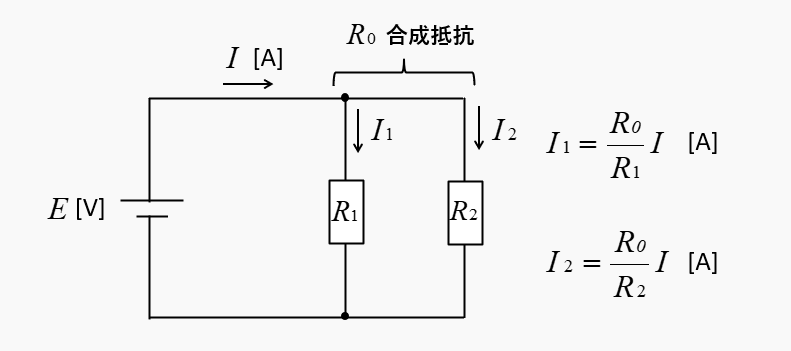
各抵抗に流れる電流の求め方
合成抵抗を \(R_0\)、それぞれの抵抗を \(R_1\)、\(R_2\)、回路に流れる電流を \(I\) とすると、各抵抗に流れる電流は、次のようになります。
\(I_1=\cfrac{R_0}{R_1}I\) [A]
\(I_2=\cfrac{R_0}{R_2}I\) [A]
抵抗が2個の並列接続のときは、次の式から求められます。
\(I_1=\cfrac{R_2}{R_1+R_2}I\) [A]
\(I_2=\cfrac{R_1}{R_1+R_2}I\) [A]
合成抵抗
抵抗 \(R_1\)、\(R_2\) が並列接続なので、合成抵抗 \(R_0\) は、和分の積から
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\) [Ω]
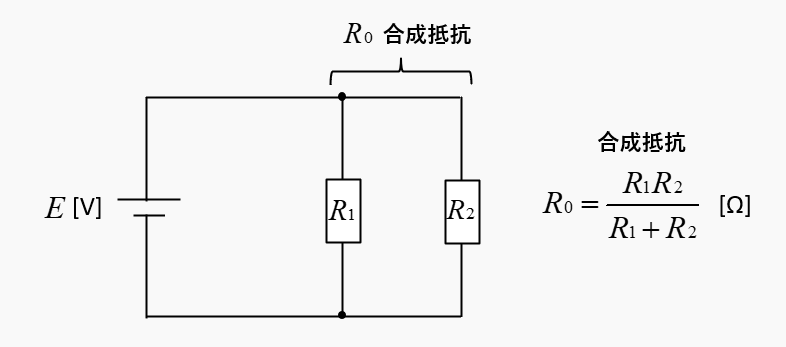
2個の抵抗に分流される電流の求め方
抵抗 \(R_1\)、\(R_2\) と電流 \(I\) が既知の値とすると、合成抵抗 \(R_0\) も計算できます。
電源電圧は \(E=R_0I\) なので
抵抗 \(R_1\) に流れる電流は \(I_1=\cfrac{E}{R_1}\) です。
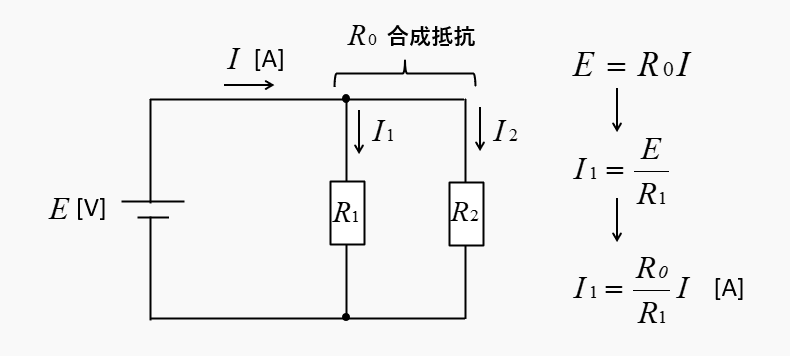
\(I_1=\cfrac{E}{R_1}\) に、電源電圧 \(E=R_0I\) を代入すると
\(I_1=\cfrac{R_0}{R_1}I\)
同様にして
\(I_2=\cfrac{R_0}{R_2}I\) となります。
分流の法則を式で表したものと同じになります。
\(求める分流の値=\)\(\cfrac{合成抵抗}{求める分流の抵抗}×回路に流れる電流\)
抵抗が2個の並列接続のときだけ、次の式が使える
\(I_1=\cfrac{R_0}{R_1}I\) に、合成抵抗 \(R_0=\cfrac{R_1R_2}{R_1+R_2}\) を代入すると
\(I_1=\cfrac{R_2}{R_1+R_2}I\) [A]
同様に、\(I_2=\cfrac{R_0}{R_2}I\) に、合成抵抗 \(R_0=\cfrac{R_1R_2}{R_1+R_2}\) を代入すると
\(I_2=\cfrac{R_1}{R_1+R_2}I\) [A] となります。
2個の抵抗が並列接続された分流の法則の例題
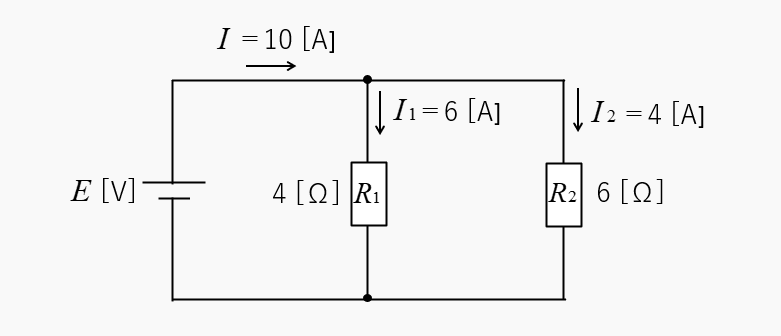
図のような回路の、抵抗に分流される電流 \(I_1\)、\(I_2\) を求めよ。
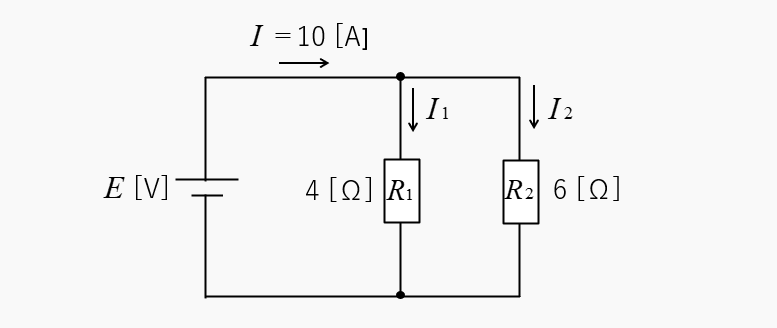
合成抵抗は、和分の積から
\(R_0=\cfrac{R_1R_2}{R_1+R_2}\)
\(R_0=\cfrac{4×6}{4+6}=\cfrac{24}{10}\) [Ω]
回路に流れる電流は、10 A と分かっているので、分流の法則の式に数値を代入すると
\(I_1=\cfrac{R_0}{R_1}I=\cfrac{R_2}{R_1+R_2}I\) [A]
\(I_1=\cfrac{\cfrac{24}{10}}{4}×10=6\) [A]
\(I_2=\cfrac{R_0}{R_2}I=\cfrac{R_1}{R_1+R_2}I\) [A]
\(I_2=\cfrac{\cfrac{24}{10}}{6}×10=4\) [A] になります。
各抵抗に流れる電流は、図のようになります。
3個の抵抗が並列接続された分流の法則
3個の抵抗が並列接続された場合のそれぞれの抵抗に流れる電流は、回路に流れる電流と各抵抗値が分かれば「分流の法則」で求めることができます。
各抵抗に流れる電流の求め方
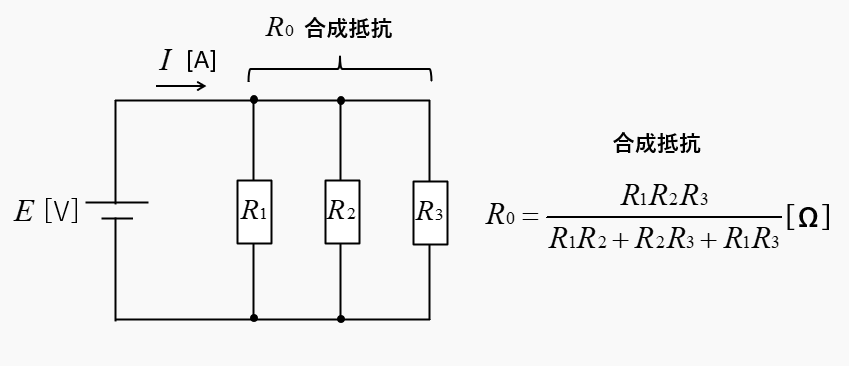
合成抵抗を \(R_0\)、それぞれの抵抗を \(R_1\)、\(R_2\)、\(R_3\)、回路に流れる電流を \(I\) とすると、次のようになります。
\(I_1=\cfrac{R_0}{R_1}I\) [A]
\(I_2=\cfrac{R_0}{R_2}I\) [A]
\(I_3=\cfrac{R_0}{R_3}I\) [A]
抵抗が3個の並列接続のときは、次の式から求められます。
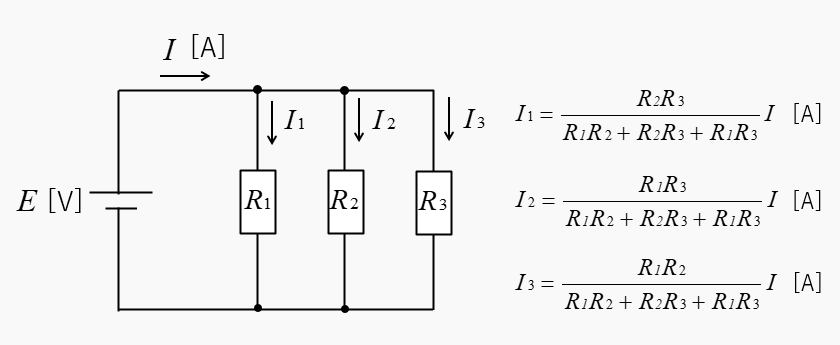
\(I_1=\cfrac{R_2R_3}{R_1R_2+R_2R_3+R_1R_3}I\)
\(I_2=\cfrac{R_1R_3}{R_1R_2+R_2R_3+R_1R_3}I\)
\(I_3=\cfrac{R_1R_2}{R_1R_2+R_2R_3+R_1R_3}I\)
合成抵抗
抵抗 \(R_1\)、\(R_2\)、\(R_3\)が並列接続なので、合成抵抗 \(R_0\) は合成抵抗の公式から
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}\)
式を変形して
\(R_0=\cfrac{R_1R_2R_3}{R_1R_2+R_2R_3+R_1R_3}\) [Ω]
3個の抵抗に分流される電流の求め方
抵抗 \(R_1\)、\(R_2\)、\(R_3\) と電流 \(I\) が既知の値とすると、合成抵抗 \(R_0\) も計算できます。
電源電圧は \(E=R_0I\)
抵抗 \(R_1\) に流れる電流は、\(I_1=\cfrac{E}{R_1}\) です。
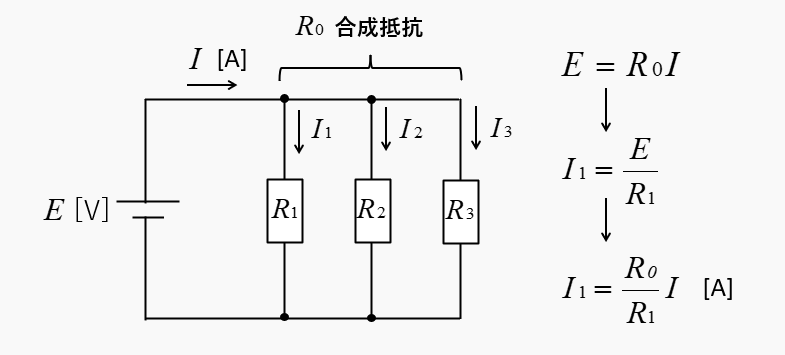
\(I_1=\cfrac{E}{R_1}\) に、電源電圧 \(E=R_0I\) を代入すると
\(I_1=\cfrac{R_0}{R_1}I\)
同様にして
\(I_2=\cfrac{R_0}{R_2}I\)
\(I_3=\cfrac{R_0}{R_3}I\) となります。
分流の法則を式で表したものと同じになります。
\(求める分流の値=\)\(\cfrac{合成抵抗}{求める分流の抵抗}×回路に流れる電流\)
抵抗が3個の並列接続のときだけ、次の式が使える
\(I_1=\cfrac{R_0}{R_1}I\) に、合成抵抗 \(R_0=\cfrac{R_1R_2R_3}{R_1R_2+R_2R_3+R_1R_3}\) を代入すると
\(I_1=\cfrac{R_2R_3}{R_1R_2+R_2R_3+R_3R_1}I\) [A]
同様に、\(I_2=\cfrac{R_0}{R_2}I\) に、合成抵抗 \(R_0=\cfrac{R_1R_2R_3}{R_1R_2+R_2R_3+R_1R_3}\) を代入すると
\(I_2=\cfrac{R_1R_3}{R_1R_2+R_2R_3+R_3R_1}I\) [A]
同様に、\(I_3=\cfrac{R_0}{R_3}I\) に、合成抵抗 \(R_0=\cfrac{R_1R_2R_3}{R_1R_2+R_2R_3+R_1R_3}\) を代入すると
\(I_3=\cfrac{R_1R_2}{R_1R_2+R_2R_3+R_3R_1}I\) [A] となります。
3個の抵抗が並列接続された分流の法則の例題
図のような回路の、抵抗に分流される電流 \(I_1\)、\(I_2\)、\(I_3\) を求めよ。
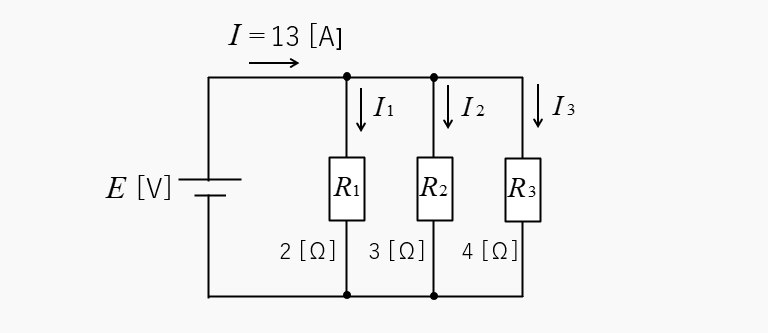
合成抵抗は、合成抵抗の並列接続の公式から
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cfrac{1}{R_3}\) を変形して
\(R_0=\cfrac{R_1R_2R_3}{R_1R_2+R_2R_3+R_1R_3}\)
\(R_0=\cfrac{2×3×4}{2×3+3×4+2×4}=\cfrac{12}{13}\) [Ω]
回路に流れる電流は、13 A なので分流の法則の式に数値を代入すると
\(I_1=\cfrac{R_0}{R_1}I\) [A]
\(I_1=\cfrac{\cfrac{12}{13}}{2}×13=6\) [A]
\(I_2=\cfrac{R_0}{R_2}I\) [A]
\(I_2=\cfrac{\cfrac{12}{13}}{3}×13=4\) [A]
\(I_3=\cfrac{R_0}{R_3}I\) [A]
\(I_3=\cfrac{\cfrac{12}{13}}{4}×13=3\) [A] になります。
各抵抗に流れる電流は、図のようになります。
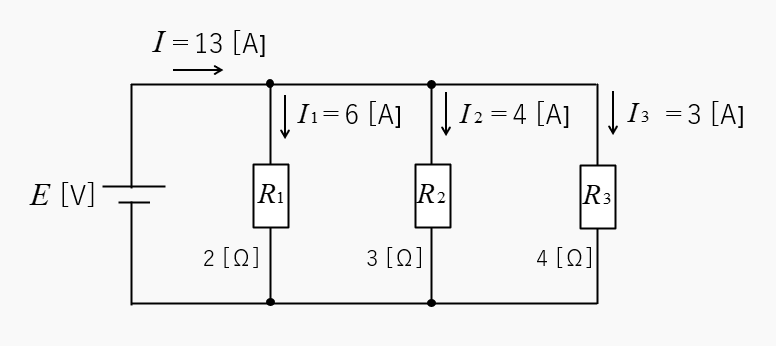
\(n\) 個の抵抗が並列接続された分流の法則
\(I_1=\cfrac{R_0}{R_1}I\) [A]
\(I_2=\cfrac{R_0}{R_2}I\) [A]
↓
\(I_n=\cfrac{R_0}{R_n}I\) [A]
合成抵抗
抵抗が \(n\) 個の並列接続なので、合成抵抗 \(R_0\) は
\(\cfrac{1}{R_0}=\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cdots+\cfrac{1}{R_n}\) [Ω]
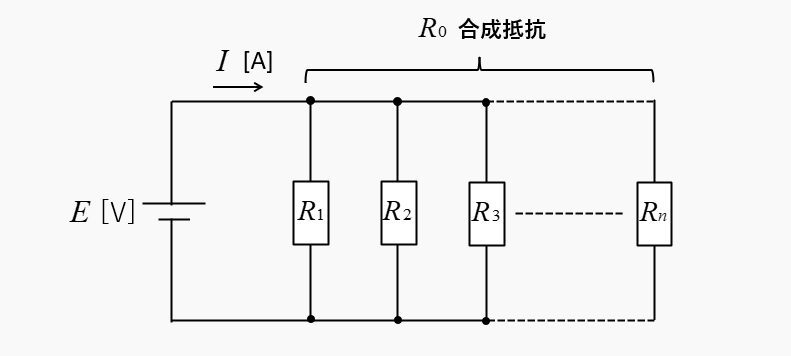
n個の抵抗に分流される電流の求め方
\(n\) 個の抵抗の値と電流 \(I\) が既知の値とすると、合成抵抗 \(R_0\) も計算できます。
電源電圧は、\(E=R_0I\) なので
抵抗 \(R_1\) に流れる電流は \(I_1=\cfrac{E}{R_1}\) です。
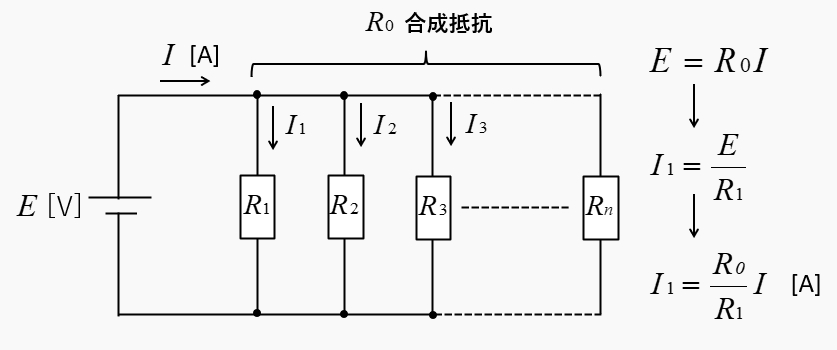
\(I_1=\cfrac{E}{R_1}\) に、電源電圧 \(E=R_0I\) を代入すると
\(I_1=\cfrac{R_0}{R_1}I\)
同様にして
\(I_2=\cfrac{R_0}{R_2}I\)
\(I_3=\cfrac{R_0}{R_3}I\)
↓
\(I_n=\cfrac{R_0}{R_n}I\) となります。
分流の法則を式で表したものと同じになります。
\(求める分流の値=\)\(\cfrac{合成抵抗}{求める分流の抵抗}×回路に流れる電流\)
まとめ
分流の法則は、並列接続の各抵抗に分流する電流を求める法則です。一般的な式で表すと次のようになります。
\(求める分流の値=\)\(\cfrac{合成抵抗}{求める分流の抵抗}×回路に流れる電流\)
合成抵抗の求め方(直列と並列の公式)
【分圧の法則】抵抗による電圧の分圧
コンダクタンスで計算する電流の分流
【初心者向け】並列回路の電圧・電流・抵抗の関係をわかりやすく解説!