分圧の法則とは、直列回路の抵抗に掛かる電圧の法則です。抵抗の大きさに比例して、電源電圧が分かれることを、電圧の分圧と呼びます。
分圧の法則は、電源電圧がそれぞれの抵抗に分圧する電圧を求める法則
分圧の法則とは?

電源電圧が抵抗の大きさに比例して、電圧が分圧されることを「分圧の法則」といいます。
電圧がそれぞれの抵抗に、比例して分圧されます。
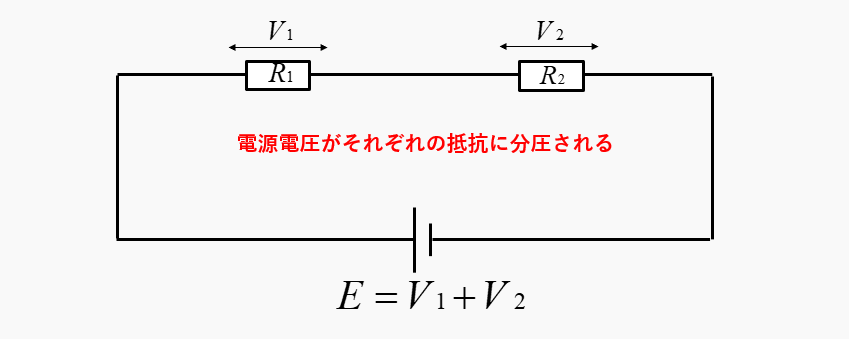
分圧の法則を式にすると、次のようになります。
\(求める分圧の値=\)\(\cfrac{求める分圧の抵抗}{合成抵抗}×電源電圧\)
分圧の法則は、「起電力の和は電圧降下の和に等しい」という キルヒホッフの第2法則 と一致します。
分圧の法則の公式はどうやって求めるの?
抵抗の直列回路に電流が流れると、抵抗で電圧降下が起こります。電圧降下はそれぞれの抵抗で発生しますので、電圧降下を足したものが電源電圧と等しくなります。
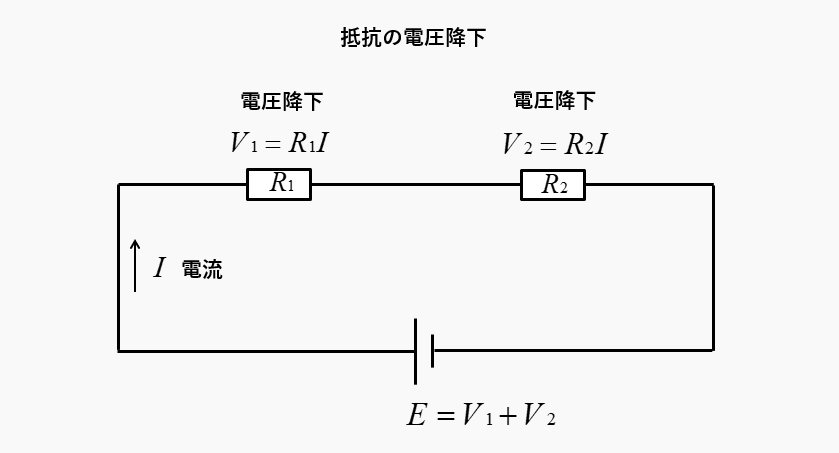
抵抗の電圧降下を知るには、回路を流れる電流が分かれば求めることができます。直列回路の全体の抵抗が分かれば、オームの法則から、回路に流れる電流を計算することができます。
直列回路の合成抵抗は、それぞれの抵抗を足せば良いので
\(R_0=R_1+R_2\) になります。
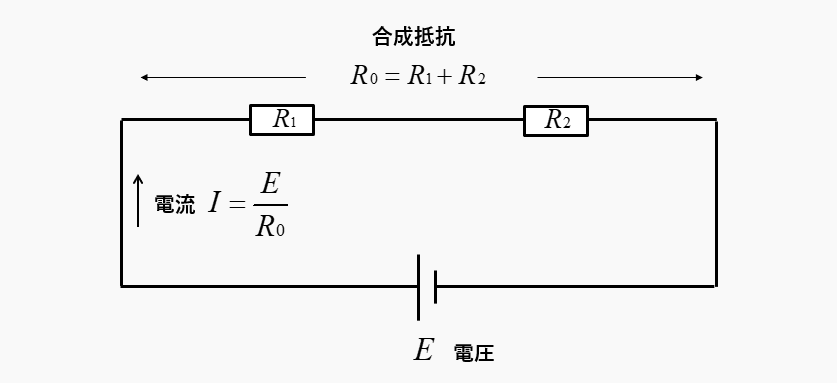
各抵抗に分圧される電圧
合成抵抗は、\(R_0=R_1+R_2\)
回路に流れる電流は、\(I=\cfrac{E}{R_0}\) ですから
\(R_1\) の分圧は、\(V_1=R_1I=\cfrac{R_1}{R_1+R_2}E\)
\(R_2\) の分圧は、\(V_2=R_2I=\cfrac{R_2}{R_1+R_2}E\) になります。
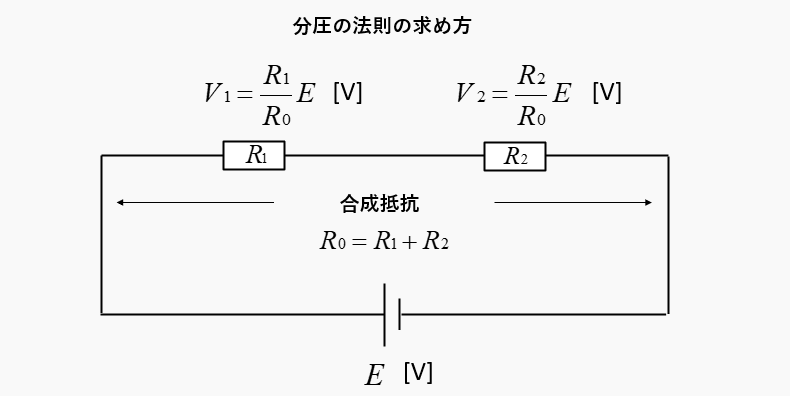
求める抵抗の分圧は、合成抵抗と電源電圧が分かれば求められる。
\(求める分圧の値=\)\(\cfrac{求める分圧の抵抗}{合成抵抗}×電源電圧\)
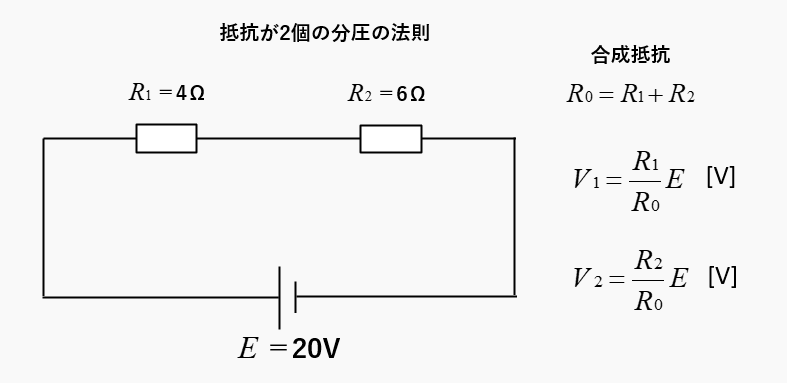
抵抗が2個の分圧の法則
\(求める分圧の値=\)\(\cfrac{求める分圧の抵抗}{合成抵抗}×電源電圧\)
図のような、抵抗が2個のときの分圧を求めるには、分圧の法則の式に代入すれば求められます。
合成抵抗は、4 + 6 なので 10Ω です。
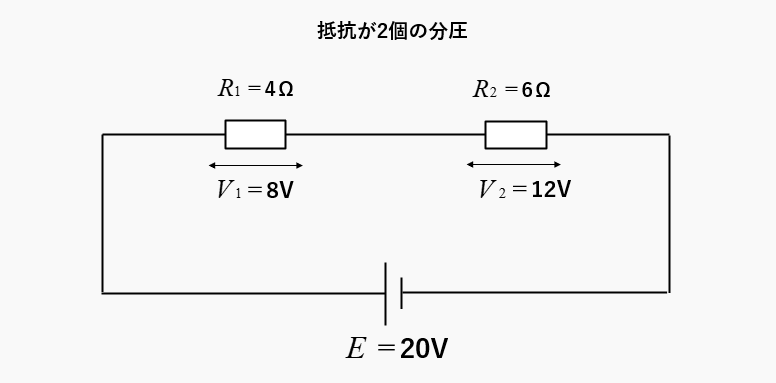
抵抗 \(R_1\) に分圧される電圧は
\(V_1=\cfrac{4}{4+6}×20=8\) [V]
抵抗 \(R_2\) に分圧される電圧は
\(V_2=\cfrac{6}{4+6}×20=12\) [V]
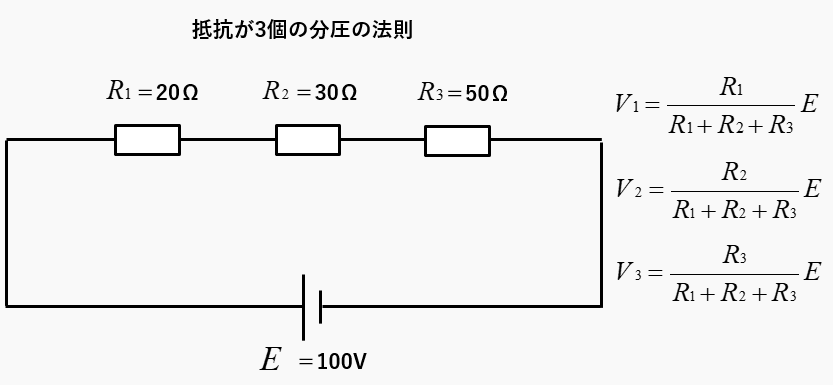
抵抗が3個の分圧の法則
\(求める分圧の値=\)\(\cfrac{求める分圧の抵抗}{合成抵抗}×電源電圧\)
図のような、抵抗が3個のときの分圧を求めるには、分圧の法則の式に代入すれば求められます。
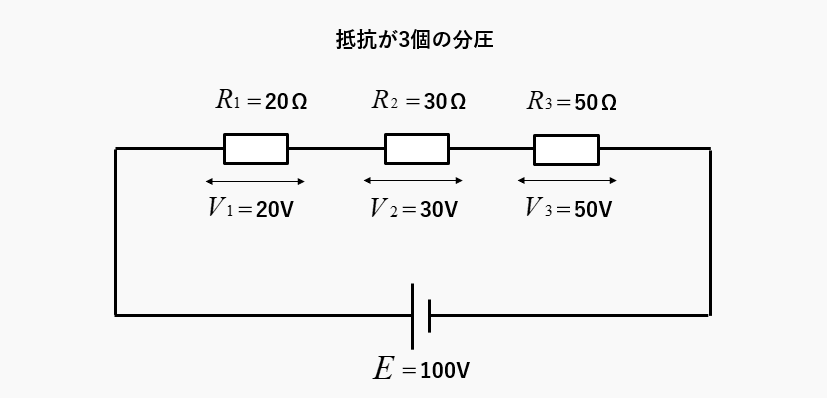
抵抗 \(R_1\) に分圧される電圧は
\(V_1=\cfrac{20}{20+30+50}×100=20\) [V]
抵抗 \(R_2\) に分圧される電圧は
\(V_2=\cfrac{30}{20+30+50}×100=30\) [V]
抵抗 \(R_3\) に分圧される電圧は
\(V_3=\cfrac{50}{20+30+50}×100=50\) [V]
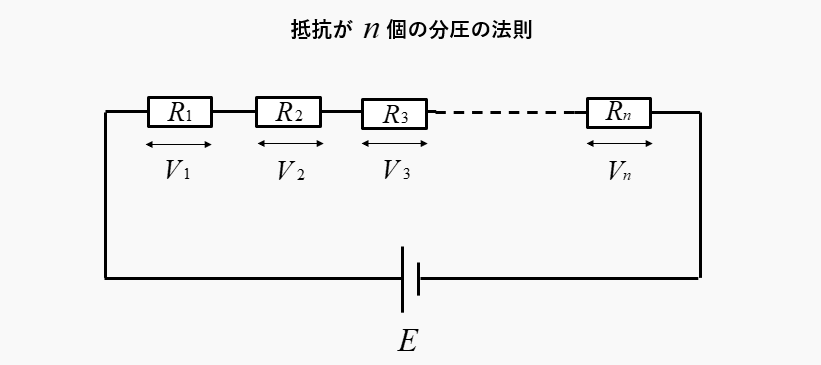
抵抗が \(n\) 個の分圧の法則
\(求める分圧の値=\)\(\cfrac{求める分圧の抵抗}{合成抵抗}×電源電圧\)
図のように、抵抗が \(n\) 個のときの分圧を求めるときも、同様に分圧の法則の式に代入すれば求められます。
抵抗 \(R_1\) に分圧される電圧は
\(V_1=\)\(\cfrac{R_1}{R_1+R_2+R_3+\cdots+R_n}×E\) [V]
抵抗 \(R_2\) に分圧される電圧は
\(V_2=\)\(\cfrac{R_2}{R_1+R_2+R_3+\cdots+R_n}×E\) [V]
抵抗 \(R_3\) に分圧される電圧は
\(V_3=\)\(\cfrac{R_3}{R_1+R_2+R_3+\cdots+R_n}×E\) [V]
抵抗 \(R_n\) に分圧される電圧は
\(V_n=\)\(\cfrac{R_n}{R_1+R_2+R_3+\cdots+R_n}×E\) [V]
まとめ
\(求める分圧の値=\)\(\cfrac{求める分圧の抵抗}{合成抵抗}×電源電圧\)