- スター結線の特徴
- スター結線の線間電圧の求め方
- スター結線の電流の瞬時値の和は0(ゼロ)になる
- 記号法による表示
について説明しています。
スター結線の特徴
図は三相交流電源と負荷の接続を スター結線(Y-Y結線) にしたものです。

相電圧と線間電圧
- 端子 \(ab、bc、ca\) の各相を 相 といいます。
- 各相の起電力 \(E_a、E_b、E_c\) を 相電圧 といいます。
- 各線間の電圧 \(V_{ab}、V_{bc}、V_{ca}\) を 線間電圧 といいます。
相電流と線電流
- 各相を流れる電流 \(I_a、I_b、I_c\) を 相電流 といいます。
- 各線を流れる電流 を 線電流 といいます。
■ 重要
スター結線では
線間電圧 \(=\sqrt3 ×\) 相電圧 になります。
相電流=線電流 になります。
線間電圧 \(V_{ab}、V_{bc}、V_{ca}\) は 相電圧 \(E_a、E_b、E_c\) の ルート3倍になります。
線電流 は 相電流 \(I_a、I_b、I_c\) と等しくなります。
図の中の 電圧の矢印の向き は 電位の高さを表わしていて 矢印の先の方が電位が高く なります。
また、各相の起電力は、互いに \(\cfrac{2π}{3}\) [rad] ラジアン の位相差があります。
スター結線電源の各相の起電力と各端子間の電圧

端子 \(ab\) 間の電位の求め方
電源の端子 \(a\) と端子 \(b\) 間の線間電圧は、端子 \(b\) を基準にした場合の端子 \(a\) の電位のことです。
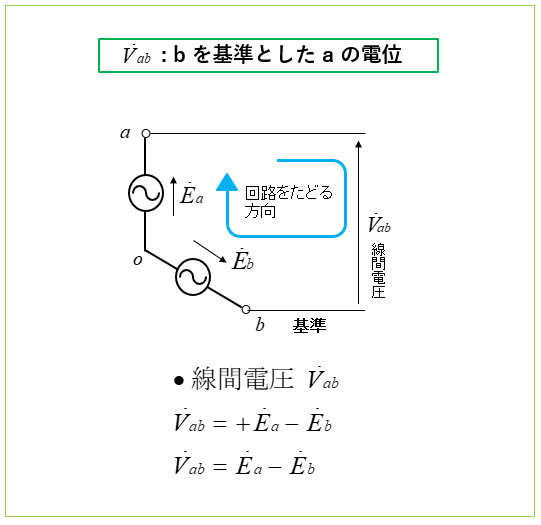
■ メモ
- \(E_a\) は回路をたどる方向と 同方向 なので、符号は(+)になる。
- \(E_b\) は回路をたどる方向と 逆方向 なので、符号は(-)となる。
- ab間の線間電圧 \(V_{ab}=\) (aの電位)-(bの電位) \(=E_a-E_b\)
- bc間の線間電圧 \(V_{bc}=\) (bの電位)-(cの電位) \(=E_b-E_c\)
- ca間の線間電圧 \(V_{ca}=\) (cの電位)-(aの電位) \(=E_c-E_a\)
■ \({V}_{ab}\) が意味すること
添字の \(ab\) は後ろの「文字\(b\)」を基準とした場合の「前の文字\(a\)」の電位を意味します。
スター結線の線間電圧の求め方
線間電圧 \(V_{ab}\) は \(E_a-E_b\) になります。
図のように、ベクトル \(E_a\) とベクトル \(-E_b\) を合成すれば線間電圧 \(V_{ab}\) の ベクトル を求めることができます。
\(-E_b\) は \(E_b\) と同じ大きさで、方向が反対のベクトルになります。

スター結線の線間電圧と相電圧のベクトル図
電源の相電圧 \(E_a、E_b、E_c\) が対称三相交流電圧であれば、線間電圧 \(V_{ab}、V_{bc}、V_{ca}\) も対称三相交流電圧になります。
相電圧も線間電圧も互いに \(\cfrac{2π}{3}\) [rad] の 位相差 があります。
線間電圧 は 相電圧 より \(\cfrac{π}{6}\) [rad] 進んでいます。
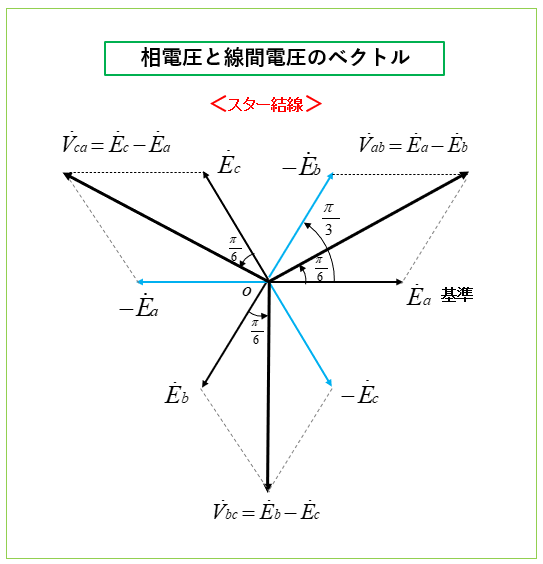
スター結線の線間電圧は相電圧のルート3倍になる
ベクトル図から スター結線の線間電圧は相電圧のルート3倍 になることを求めます。
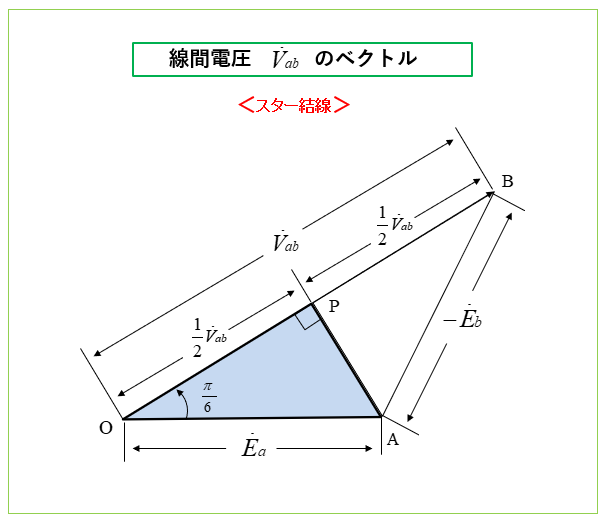
- 三角形 ABO は、辺 BO が線間電圧 \(V_{ab}\) 辺 AO と辺 AB が相電圧 \(E_a\) と \(-E_b\) なので、大きさが等しい「二等辺三角形」になります。
- P点は 辺 BO を二等分します。
辺POの長さは
\(PO=\cfrac{1}{2}V_{ab}\) になります。 - 直角三角形 APO で、∠AOPは \(\cfrac{π}{6}\) ですから
\(\cos\cfrac{π}{6}\) は、次のようになります。
\(\cos\cfrac{π}{6}\)\(=\cfrac{PO}{AO}\)\(=\cfrac{\cfrac{1}{2}V_{ab}}{E_a}\cdots(1)\) - 式(1)を変形して \(V_{ab}=\) にすると
\(V_{ab}=2E_a\cos\cfrac{π}{6}\)
\(=2E_a×\cfrac{\sqrt{3}}{2}\)\(=\sqrt{3}{E_a}\)
\(V_{ab}=\sqrt{3}{E_a}\) になります。
■ メモ
三角関数の値 \(\cos\cfrac{π}{6}=\cfrac{\sqrt{3}}{2}\)
対称三相交流であれば、各相電圧は等しいので、\(E_a=E_b=E_c\) です。
相電圧を \(E_p\) とすると \(E_p=E_a=E_b=E_c\) になります。
\(V_{ab}=\sqrt{3}{E_p}\) [V]
\(V_{bc}=\sqrt{3}{E_p}\) [V]
\(V_{ca}=\sqrt{3}{E_p}\) [V] になります。
スター結線の線間電圧は
線間電圧 \(=\sqrt{3}\) × 相電圧 になります。
スター結線の各相に流れる電流の瞬時値の和は 0(ゼロ)になる
図の中性線点 \(o-o\) に流れる電流 \(\dot{I_a}+\dot{I_b}+\dot{I_c}\) の合成電流は、大きさが等しく、互いに \(\cfrac{2π}{3}\quad\rm[rad]\) の位相差がある対称三相交流になります。

電流の瞬時値の和を、\(i_0\) 各相の電流を \(i_a、i_b、i_c\) とすると、\(i_0\) の値は 0(ゼロ)なります。
\(i_0=i_a+i_b+i_c=0\)
\(i_0=I_m\sin ωt+I_m\sin\left(ωt-\cfrac{2π}{3}\right)\)\(+I_m\sin\left(ωt-\cfrac{4π}{3}\right)\)
\(i_0=I_m\{\sin ωt\)\(+(\sin ωt \cos\cfrac{2π}{3}-\cos ωt \sin\cfrac{2π}{3}\)\(+\sin ωt \cos\cfrac{4π}{3}-\cos ωt \sin\cfrac{4π}{3})\}\cdots(1)\)
ここで、三角関数の値から
\(\cos\cfrac{2π}{3}=-\cfrac{1}{2}\)
\(\sin\cfrac{2π}{3}=\cfrac{\sqrt3}{2}\)
\(\cos\cfrac{4π}{3}=-\cfrac{1}{2}\)
\(\sin\cfrac{4π}{3}=-\cfrac{\sqrt3}{2}\) なので、式(1)は次のようになります。
\(i_0=I_m\{\sin ωt+(-\cfrac{1}{2}\sin ωt-\cfrac{\sqrt3}{2}\cos ωt\)\(-\cfrac{1}{2}\sin ωt+\cfrac{\sqrt3}{2}\cos ωt)\}\)
\(i_0=I_m(\sin ωt-\sin ωt)=0\)
スター結線の相電圧と線間電圧を記号法で求める
スター結線の相電圧の大きさを \(E\) とすると、各相電圧は次のようになります。
\(E_a=E\)
\(E_b=E\left(-\cfrac{1}{2}-j\cfrac{\sqrt{3}}{2}\right)\)
\(E_c=E\left(-\cfrac{1}{2}+j\cfrac{\sqrt{3}}{2}\right)\)
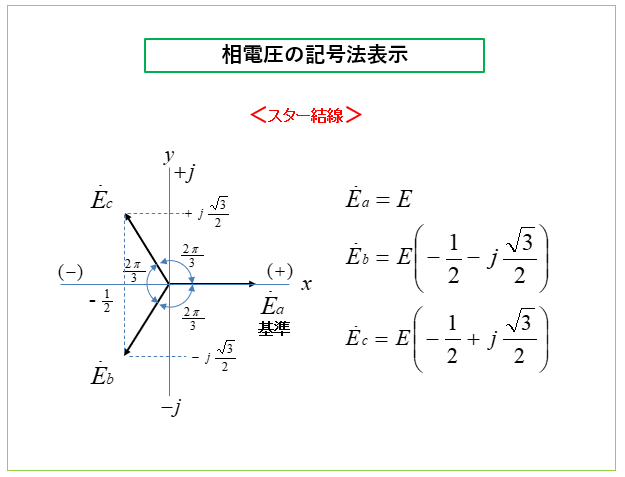
スター結線の各線間電圧は、次のようになります。
\(V_{ab}\)\(=E_a-E_b\)\(=E-E\left(-\cfrac{1}{2}-j\cfrac{\sqrt{3}}{2}\right)\)\(=E\left(\cfrac{3}{2}+j\cfrac{\sqrt{3}}{2}\right)\)
\(V_{bc}\)\(=E_b-E_c\)\(=E\left(-\cfrac{1}{2}-j\cfrac{\sqrt{3}}{2}\right)-E\left(-\cfrac{1}{2}+j\cfrac{\sqrt{3}}{2}\right)\)\(=-j\sqrt{3}E\)
\(V_{ca}\)\(=E_c-E_a\)\(=E\left(-\cfrac{1}{2}+j\cfrac{\sqrt{3}}{2}\right)-E\)\(=E\left(-\cfrac{3}{2}+j\cfrac{\sqrt{3}}{2}\right)\)
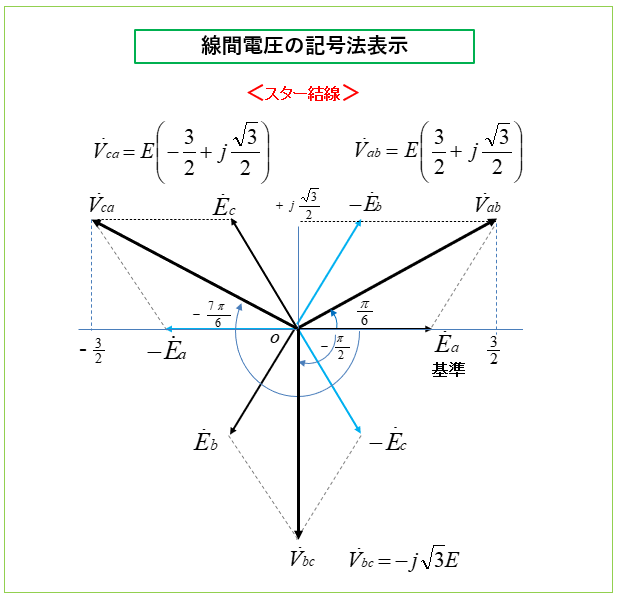
\(E_a\) を基準として、\(V_{ab}、V_{bc}、V_{ca}\) の位相角 \(θ_{ab}、θ_{bc}、θ_{ca}\) は、次のようになります。
\(θ_{ab}\)\(=tan^{-1}\cfrac{\cfrac{\sqrt{3}}{2}}{\cfrac{3}{2}}\)\(=tan^{-1}\cfrac{1}{\sqrt{3}}\)\(=\cfrac{π}{6}\)
\(θ_{bc}\)\(=-\cfrac{π}{2}\)
\(θ_{ca}\)\(=tan^{-1}\cfrac{\cfrac{\sqrt{3}}{2}}{\cfrac{-3}{2}}\)\(=-\cfrac{7π}{6}\)
スター結線のまとめ


スター結線の線間電圧は、次のようになります。
\(V_{ab}=E_a-E_b\)
\(V_{bc}=E_b-E_c\)
\(V_{ca}=E_c-E_a\)
■ スター結線の特徴
線間電圧 \(=\sqrt{3}\) × 相電圧\) [V]
線間電圧は相電圧より、位相が \(\cfrac{π}{6}\) [rad] 進む。
相電圧は線間電圧より、位相が \(\cfrac{π}{6}\) [rad] 遅れると見ることもできます。
また 線電流=相電流 になります。
練習問題
問題1
線間電圧 \(200\) [V] の三相3線式回路に \(Z=8+j6\) [Ω] の対称負荷を星形に接続してあります。
この場合の相電圧と相電流を求めよ。
<解答例>
問題文を図に表すと次のようになります。
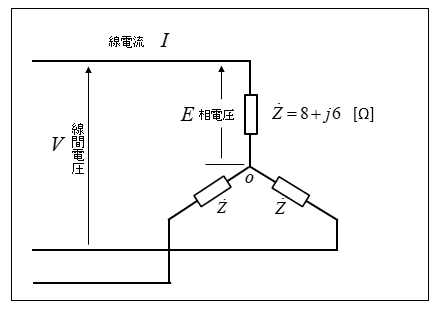
スター結線では、線間電圧 \(V\) と相電圧 \(E\) の関係は
\(V=\sqrt{3}E\) [V] になります。
したがって相電圧 \(E\) は
\(E=\cfrac{V}{\sqrt{3}}\)\(=\cfrac{200}{\sqrt{3}}≒115\) [V]
線電流 \(I\) は
\(I=\cfrac{E}{|Z|}\)\(=\cfrac{E}{\sqrt{R^2+X^2}}\)
\(=\cfrac{20}{\sqrt{3}}\)\(≒11.5\) [A] になります。