静電気に関するクーロンの法則 と同じように
磁気においても 磁気に関するクーロンの法則 があります。
ここでは、磁気に関するクーロンの法則について説明します。
クーロンの法則の力の向き
磁石で両端の最も磁気の強いところを 磁極 といいます。

磁極には N極 と S極 があり
北を指す磁極を N極(正極、+極)
南を指す磁極を S極(負極、-極) といい
N極 と S極 は 一対で存在 します。
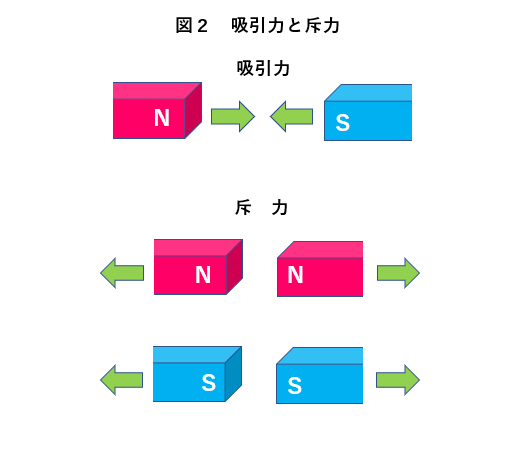
★ 図2のように N極 と S極 のように異なる磁極の間には 吸引力 が働きます。
★ N極同士 または S極同士 のように同じ磁極の間には 斥力 が働きます。
■ 点磁極
磁極は電荷のように、プラス、マイナスが単独で存在しませんが
非常に細く長い磁石を仮定すれば、単独の磁極として扱うことができます。
このような、磁極の大きさを無視したものを 点磁極 として考えます。

■ 磁極の強さ
磁極の強さの記号は \(m\) 、単位は [Wb] ウェーバ を使います。
磁気に関するクーロンの法則
2つの点磁極の間に働く力を 磁気に関するクーロンの法則 といいます。
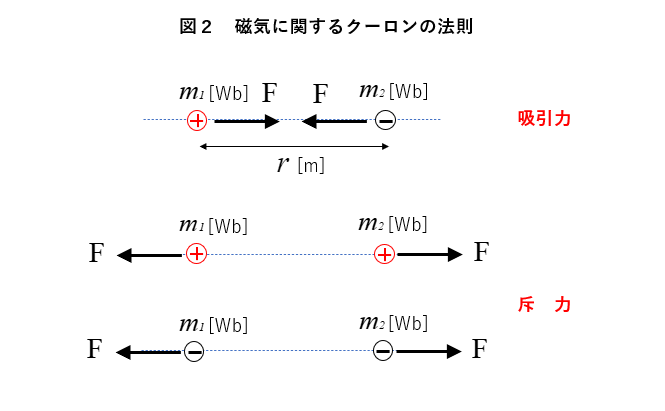
磁極の強さを \(m_1、m_2\) [Wb]
磁極間の距離を \(r\) [m] とすると
磁極に働く力 \(F\) [N] は
\(F=k\cfrac{m_1m_2}{r^2}\) [N]
\(F=6.33×10^4×\cfrac{m_1m_2}{r^2}\) [N]
磁気に関するクーロンの法則は2つの磁極間に働く力は
2つの磁極の積に比例し、磁極感の距離の2乗に反比例するというものです。
透磁率は磁気を通す比率を表します。
\(k=\cfrac{1}{4πμ_0}≒6.33×10^4\) [N・m2/Wb2]\(\cdots\)定数
\(μ_0=4π×10^{-7}\) [H/m]\(\cdots\)真空の透磁率
\(μ=μ_0μ_r\) [H/m]\(\cdots\)透磁率で「ミュー」と読みます。
\(μ_r=\cfrac{μ}{μ_0}\cdots\)比透磁率 空気中では、\(μ_r=1\) です。
\(k=\cfrac{1}{4πμ}\cdots\)透磁率 \(μ\) の媒質中の定数
クーロンの法則は透磁率 \(μ\) の媒質中では 次の公式になります。
\(F=k\cfrac{m_1m_2}{μ_rr^2}\) [N]
練習問題
問題1
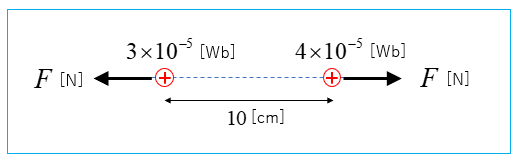
図のように、真空中において二つの点磁極を \(10\) [cm] 離しておいた時
両磁極間に働く力 \(F\) [N] を求めよ。
<解答例>
クーロンの法則から
\(F=k\cfrac{m_1m_2}{r^2}\) [N]
\(F=6.33×10^4×\cfrac{3×10^{-5}×4×10^{-5}}{0.1^2}\) [N]
\(F=7.596×10^{-3}\) [N]
以上で「磁気に関するクーロンの法則」の説明を終わります。