クーロンの法則は2つの電荷間に働く クーロン力(静電気力)を求める公式です。
クーロンの法則で、働く力の方向や大きさについて説明します。
クーロンの法則
2つの点電荷の間に働く力を クーロンの法則 といいます。
\(F=k\cfrac{Q_1Q_2}{r^2}\) [N]
\(F=9×10^9×\cfrac{Q_1Q_2}{r^2}\) [N]
電荷量を \(Q_1、Q_2\) [C]
電荷間の距離を \(r\) [m] とすると
電荷に働く力 \(F\) [N] は
\(F=k\cfrac{Q_1Q_2}{r^2}\) [N]
\(F=9×10^9×\cfrac{Q_1Q_2}{r^2}\) [N]
★ クーロンの法則は誘電率 \(ε\) の媒質中では 次の公式になります。
\(F=k\cfrac{Q_1Q_2}{ε_rr^2}\) [N]
誘電率は電荷の貯めやすさの比率を表します。
\(k=\cfrac{1}{4\piε_0}=9×10^9\) [N・m2/C2]\(\cdots\)定数
\(ε_0=8.854×10^{-12}\) [F/m]\(\cdots\)真空の誘電率
\(ε=ε_0ε_r\) [F/m]\(\cdots\)誘電率で「イプシロン」と読みます。
\(ε_r=\cfrac{ε}{ε_0}\)\(\cdots\)比誘電率 空気中では \(ε_r=1\) です。
\(k=\cfrac{1}{4\piε}\cdots\)誘電率εの媒質中の定数
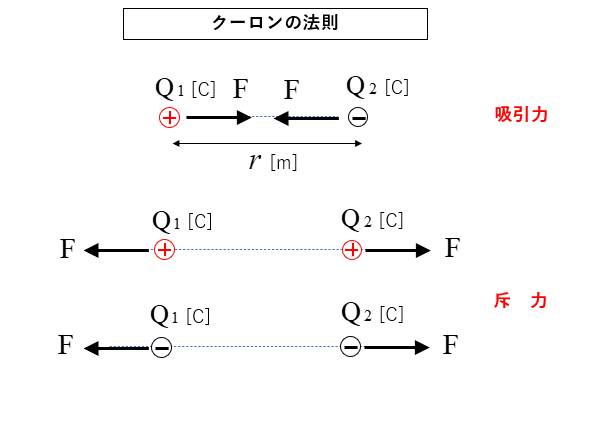
クーロンの法則の力の向き
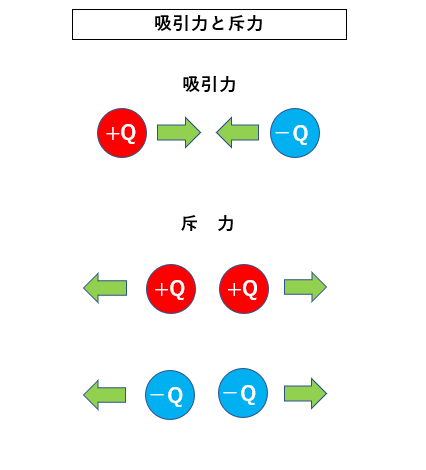
図のように 正電荷 と 負電荷 のように
異なる電荷の間には 吸引力 が働きます。
正電荷同士 または 負電荷同士 のように
同じ電荷の間には 斥力 が働きます。
■ 点電荷とは
電荷の中で、大きさ(面積や体積)を持たないけれども、電気を帯びた帯電体を点電荷と考えます。
■ 点電荷の大きさ
点電荷の大きさの記号は \(Q、q\) 単位は [C] クーロンを使います。
クーロン力の大きさ
クーロンの法則の公式に数値を当てはめて見るとわかりますが
クーロン力というのはものすごく大きい力 ということがわかります。
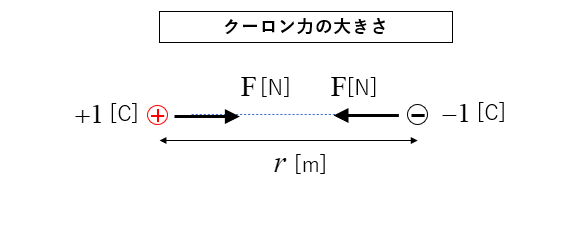
図のように +1クーロンの電荷 と -1クーロンの電荷 が
距離 1m にある場合の クーロン力 \(F\) [N] の大きさを計算してみましょう。
\(F=9×10^9×\cfrac{Q_1Q_2}{r^2}\) [N]
\(F=9×10^9×\cfrac{1×1}{1^2}=9×10^9\) [N]
静電気力(クーロン力)\(F\) [N] の大きさは
90億ニュートンとなり、ものすごく大きいということがわかりますね。
■ メモ
静電気力(クーロン力)\(F\) を計算するときに、電荷の符号を入れて計算する必要はありません。
電荷の符号が決まると力の方向も決まります。
静電気力(クーロン力)\(F\) を計算するときには、電荷の大きさを入れれば計算できます。
まとめ
■ クーロンの法則
真空中・空気中のとき
\(F=k\cfrac{Q_1Q_2}{r^2}\) [N]
\(F=9×10^9×\cfrac{Q_1Q_2}{r^2}\) [N]
\(k=\cfrac{1}{4\piε_0}=9×10^9\) [N・m2/C2]
一般的な媒質中のとき
\(F=k\cfrac{Q_1Q_2}{ε_rr^2}\) [N]
\(F=9×10^9×\cfrac{Q_1Q_2}{ε_rr^2}\) [N]
■ 誘電率
\(ε_0=8.854×10^{-12}\) [F/m]\(\cdots\)真空の誘電率
\(ε=ε_0ε_r\) [F/m]\(\cdots\)誘電率
\(ε_r=\cfrac{ε}{ε_0}\cdots\)比誘電率 空気中では \(ε_r=1\) です。
★ クーロンの法則から 電界の強さ を求めることができます。
練習問題
問題1
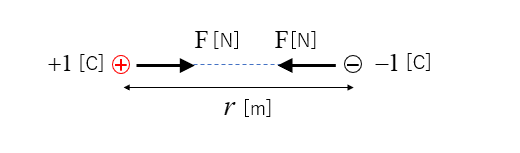
図のように、互いに1クーロンの点電荷があるとき
2つの電荷間に働く静電気力(クーロン力)が1kg重の力になるようにするには
どれだけの距離が必要か求めよ。
ただし、重力加速度を \(10\) [m/s2] とする。
<解答例>
この問題では、重力加速度が \(10\) [m/s2] なので
\(1\rm kg重=10\) [N] になります。
クーロンの法則から \(F=10\) [N]
\(F=9×10^9×\cfrac{Q_1Q_2}{ε_rr^2}\)
\(F=9×10^9×\cfrac{1×1}{r^2}=10\) [N]
\(r^2=\cfrac{9×10^9}{10}=9×10^8\)
\(r=3×10^4\) [m]
\(r=30\) [km]
したがって、電荷間に働く力を1kg重の力になるようにするには
2つの電荷を30キロメートルも離す必要があります。
このことからも、静電気力(クーロン力)がいかに大きいかがわかります。
問題2
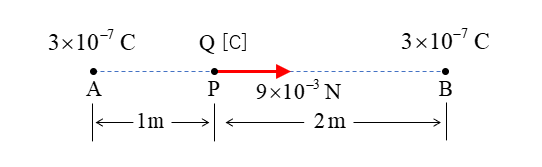
図のように、真空中の3m離れた2点 A,B に
それぞれ \(3×10^{-7}\) [C] の正の点電荷がある。
A点とB点とを結ぶ直線上の A点から1m離れたP点に
\(Q\) [C] の正電荷を置いたとき
その点電荷にB点の方向に \(9×10^{-3}\) [N] の力が働いた。
この点電荷の値を求めよ。
ただし、真空中の誘電率を \(ε_0=\cfrac{1}{4π×9×10^9}\) [F/m] とする。
<解答例>
図のように、P点の電荷 \(Q\) [C] に働く力 \(F_A,F_B\) を求めます。
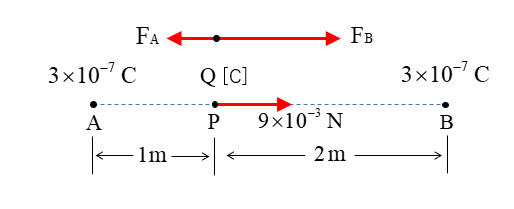
\(F_A=\cfrac{1}{4πε_0}×\cfrac{3×10^{-7}Q}{1^2}\)
\(F_B=\cfrac{1}{4πε_0}×\cfrac{3×10^{-7}Q}{2^2}\)
\(F_A,F_B\) の差が \(9×10^{-3}\) [N] から
\(\cfrac{1}{4πε_0}×\cfrac{3×10^{-7}Q}{1^2}-\cfrac{1}{4πε_0}×\cfrac{3×10^{-7}Q}{2^2}\)\(=9×10^{-3}\)
式を整理して、\(ε_0\) の数値を代入します。
\(\cfrac{3×10^{-7}Q}{4πε_0}\left(\cfrac{1}{1}-\cfrac{1}{4}\right)\)\(=9×10^{-3}\)
\(\cfrac{3×10^{-7}Q}{4πε_0}×\cfrac{3}{4}\)\(=9×10^{-3}\)
\(Q=\cfrac{4×4π×\cfrac{1}{4π×9×10^9}×9×10^{-3}}{3×3×10^{-7}}\)
\(Q=\cfrac{4}{9}×10^{-9-3+7}\)\(=\cfrac{4}{9}×10^{-5}\)
\(Q≒4.4×10^{-6}\) [C] となります。
以上で「クーロンの法則」の説明を終わります。